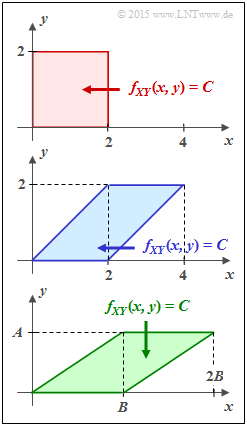
Exercise 4.5: Mutual Information from 2D-PDF
Vorgegeben sind hier die drei unterschiedlichen 2D–Gebiete fXY(x, y), die in der Aufgabe nach ihren Füllfarben mit
- rote Verbund-WDF
- blaue Verbund-WDF
- grüne Verbund-WDF
bezeichnet werden. In den dargestellten Gebieten gelte jeweils fXY(x, y) = C = const.
Die Transinformation zwischen den wertkontinuierlichen Zufallsgrößen X und Y kann unter anderem nach folgender Gleichung berechnet werden: I(X;Y)=h(X)+h(Y)−h(XY).
Für die hier verwendeten differentiellen Entropien gelten die folgenden Gleichungen: h(X)=−∫x∈supp(fX)fX(x)⋅log[fX(x)]dx, h(Y)=−∫y∈supp(fY)fY(y)⋅log[fY(y)]dy, h(XY)=−∫∫(x,y)∈supp(fXY)fXY(x,y)⋅log[fXY(x,y)]dxdy. Für die beiden Randwahrscheinlichkeitsdichtefunktionen gilt dabei: fX(x)=∫y∈supp(fY)fXY(x,y)dy,fY(y)=∫x∈supp(fX)fXY(x,y)dx. Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.2. Gegeben seien zudem folgende differentielle Entropien:
- Ist X dreieckverteilt zwischen xmin und xmax, so gilt:
h(X)=log[[:Template:e√]⋅(xmax−xmin)/2].
- Ist Y gleichverteilt zwischen ymin und ymax, so gilt:
h(Y)=log[ymax−ymin].
- Alle Ergebnisse sollen in „bit” angegeben werden. Dies erreicht man mit „log” ⇒ „log2”.
Fragebogen
Musterlösung
