Exercise 3.2Z: Bessel Spectrum

Verlauf der Besselfunktionen

Wir betrachten das komplexe Signal

$$x(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t) }\hspace{0.05cm}.$$

Beispielsweise kann man das äquivalente Tiefpass–Signal am Ausgang eines Winkelmodulators (PM, FM) in dieser Form darstellen, wenn man geeignete Normierungen vornimmt.

Die Fourierreihendarstellung lautet mit $T_0 = 2π/ω_0$:

$$x(t) = \sum_{n = - \infty}^{+\infty}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t }\hspace{0.05cm},$$

$$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}x(t) \cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$

Diese komplexen Fourierkoeffizienten können mit Hilfe der Besselfunktionen erster Art und n–ter Ordnung ausgedrückt werden:

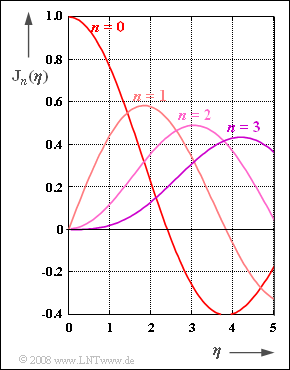
$${\rm J}_n (\eta) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$

Diese sind in der Grafik im Bereich $0 ≤ η ≤ 5$ dargestellt. Für negative Werte von $n$ erhält man:

$${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)\hspace{0.05cm}.$$

Die Reihendarstellung der Besselfunktionen lautet:

$${\rm J}_n (\eta) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (\eta/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$

Sind die Funktionswerte für $n = 0$ und $n = 1$ bekannt, so können daraus die Besselfunktionen für $n ≥ 2$ iterativ ermittelt werden:

$${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$

Hinweise:

Die Aufgabe gehört zum Kapitel Phasenmodulation.
Bezug genommen wird insbesondere auf die Seite Äquivalentes Tiefpass-Signal bei Phasenmodulation.
Die Werte der Besselfunktionen findet man in Formelsammlungen in tabellarischer Form.
Sie können zur Lösung dieser Aufgabe auch das Interaktionsmodul Werte der Besselfunktion erster Art und n–ter Ordnung nutzen.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

	$x(t)$ ist für alle Zeiten $t$ imaginär.
	$x(t)$ ist periodisch.
	Die Spektralfunktion $X(f)$ erhält man über das Fourierintegral.

	Alle $D_n$ sind gleich ${\rm J}_η(0)$.
	Es gilt $D_n = {\rm J}_n(η)$.
	Es gilt $D_n = -{\rm J}_η(n)$.

	Alle $D_n$ sind rein reell.
	Alle $D_n$ sind rein imaginär.

$D_2 \ = \ $

$D_3 \ = \ $

$D_{-2} \ = \ $

$D_{-3} \ = \ $

Musterlösung

Solution

1. $x(t)$ ist ein komplexes Signal, das nur in Ausnahmefällen reell wird, zum Beispiel zur Zeit $t = 0$. Ein rein imaginärer Wert (zu gewissen Zeiten) kann sich nur dann ergeben, wenn $η ≥ π/2$ ist. Mit $T_0 = 2π/ω_0$ gilt beispielsweise: $$ x(t + k \cdot T_0) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} (t \hspace{0.05cm}+ \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm}T_0)) } =$$ $$ = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} + \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi) } ={\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} ) } = x(t)\hspace{0.05cm}.$$ Dieses Signal ist somit periodisch. Zur Berechnung der Spektralfunktion muss deshalb die Fourierreihe und nicht das Fourierintegral herangezogen werden. Richtig ist also nur der zweite Lösungsvorschlag.

2.Die Fourierkoeffizienten lauten: $$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t) }\cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ Durch Zusammenfassen der beiden Terme und nach der Substitution $α = ω_0 · t$ erhält man: $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm} = {\rm J}_n (\eta) .$$ Richtig ist also der zweite Lösungsvorschlag.

3.Mit dem Satz von Euler können die Fourierkoeffizienten wie folgt dargestellt werden: $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha +$$ $$ + \frac{ j}{2\pi}\cdot \int_{-\pi}^{+\pi} {\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$ Der Integrand des ersten Integrals ist eine gerade Funktion von α: $$I_1 (-\alpha) = {\cos( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\cos( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}=$$ $$= {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = I_1 (\alpha) \hspace{0.05cm}.$$ Dagegen ist der zweite Integrand eine ungerade Funktion: $$I_2 (-\alpha) = {\sin( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\sin( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}=$$ $$ = -{\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = -I_2 (\alpha) \hspace{0.05cm}.$$ Somit verschwindet das zweite Integral und man erhält unter Berücksichtigung der Symmetrie: $$D_n = \frac{1}{\pi}\cdot \int_{0}^{\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$ Richtig ist somit der Lösungsvorschlag 1.

4.Entsprechend der iterativen Berechnungsformel gilt für $η = 2$: $$ D_2 = D_1 - D_0 = 0.577 - 0.224 \hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$ $$D_3 = 2 \cdot D_2 - D_1 = 2 \cdot 0.353 - 0.577 \hspace{0.15cm}\underline {= 0.129} \hspace{0.05cm}.$$

5. Aufgrund der angegebenen Symmetriebeziehung ist $D{–2} = D_2 = 0.353$ und $D{–3} = – D_3 = –0.129$.