Exercise 3.8: Modulation Index and Bandwidth

• Return to book

Tabelle der Besselfunktionen

Eine harmonische Schwingung der Form

$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$

wird winkelmoduliert und dann das einseitige Betragsspektrum $|S_+(f)|$ ermittelt.

• Mit der Nachrichtenfrequenz $f_{\rm N} = 2 \ \rm kHz$ sind folgende Spektrallinien mit folgenden Gewichten zu erkennen:

$$|S_{\rm +}(98\,{\rm kHz})| = |S_{\rm +}(102\,{\rm kHz})| = 1.560\,{\rm V}\hspace{0.05cm},$$ $$|S_{\rm +}(96\,{\rm kHz})| = |S_{\rm +}(104\,{\rm kHz})| = 1.293\,{\rm V}\hspace{0.05cm},$$

$$|S_{\rm +}(94\,{\rm kHz})| = |S_{\rm +}(106\,{\rm kHz})| = 0.594\,{\rm V}\hspace{0.05cm}.$$

Weitere Spektrallinien folgen mit jeweiligem Frequenzabstand $f_{\rm N} = 2 \ \rm kHz$, sind hier jedoch nicht angegeben und können vernachlässigt werden.

• Erhöht man die Nachrichtenfrequenz auf $f_{\rm N} = 4 \ \rm kHz$, so gibt es die dominanten Linien

$$|S_{\rm +}(100\,{\rm kHz})| = 2.013\,{\rm V}\hspace{0.05cm},$$

$$|S_{\rm +}(96\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(104\,{\rm kHz})| = 1.494\,{\rm V}\hspace{0.05cm},$$

$$|S_{\rm +}(92\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(108\,{\rm kHz})| = 0.477\,{\rm V},$$

sowie weitere, vernachlässigbare Diraclinien im Abstand $4 \ \rm kHz$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Frequenzmodulation.
• Bezug genommen wird aber auch auf das Kapitel Phasenmodulation und insbesondere auf den Abschnitt Signalverl.äufe bei Frequenzmodulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welches Modulationsverfahren liegt hier vor?

	Phasenmodulation.
	Frequenzmodulation.

2

Wie groß ist der Modulationsindex $η_2$ bei der Nachrichtenfrequenz $f_{\rm N} = 2 \ \rm kHz$?

$η_2 \ = \ $

3

Wie groß ist die Trägeramplitude?

$A_{\rm T} \ = \ $ $\ \rm V$

4

Geben Sie die Bandbreite $B_2$ an, wenn mit $f_{\rm N} = 2 \ \rm kHz$ ein Klirrfaktor $K < 1\%$ gefordert wird.

$B_2 \ = \ $ $\ \rm kHz$

5

Wie groß ist der Modulationsindex $η_4$ bei der Nachrichtenfrequenz $f_{\rm N} = 4 \ \rm kHz$?

$η_4\ = \ $

6

Welche Kanalbandbreite $B_4$ ist nun erforderlich, um $K < 1\%$ zu gewährleisten?

$B_4 \ = \ $ $\ \rm kHz$

Musterlösung

Solution

1. Es handelt sich um eine Frequenzmodulation ⇒ Antwort 2. Bei Phasenmodulation würden sich die Gewichte der Diraclinien bei der Frequenzverdopplung nicht ändern.

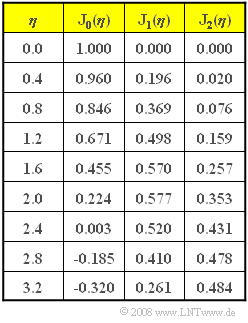
2. Die angegebene Spektralfunktion lässt aufgrund von Symmetrieeigenschaften auf die Trägerfrequenz $f_T = 100 kHz$ schließen. Da bei $f_N = 2 kHz$ die Spektrallinie bei $f_T = 100 kHz$ verschwindet, ist $η_2 ≈ 2.4$ zu vermuten. Eine Kontrolle der weiteren Impulsgewichte bestätigt das Ergebnis: $$\frac { |S_{\rm +}(f =102\,{\rm kHz})|}{ |S_{\rm +}(f =104\,{\rm kHz})|} = 1.206,\hspace{0.2cm} \frac { {\rm J}_1(2.4)}{ {\rm J}_2(2.4)}= 1.206 \hspace{0.05cm}.$$

3. Die Gewichte der Diraclinien bei $f_T + n · f_N$ lauten allgemein: $$D_n = A_{\rm T} \cdot { {\rm J}_n(\eta)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} D_1 = A_{\rm T} \cdot { {\rm J}_1(\eta)}\hspace{0.05cm}.$$ Daraus folgt $A_T = D_1/J_1(η) = 1.560 V/0.520 = 3 V$.

4. Mit der Forderung $\text{K < 1%}$ gilt folgende Faustformel (Carson–Regel): $$B_{\rm 2} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.15cm}\underline {= 17.6\,{\rm kHz}}\hspace{0.05cm}.$$ Somit stehen dem Empfänger die Fourierkoeffizienten $D_{–4}$, ....,$D_4$ zur Verfügung.

5. Bei Frequenzmodulation gilt allgemein: $$\eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.05cm}.$$ Durch Verdopplung der Nachrichtenfrequenz wird also der Modulationsindex halbiert: $η_4 = η_2/2 = 1.2$.

6. Die für $\text{K < 1%}$ erforderliche Kanalbandbreite ergibt sich nach gleicher Rechnung wie unter Punkt d) zu $B_4 = 3.2 · 8 kHz = 25.6 kHz$. Aufgrund des um den Faktor 2 kleineren Modulationsindex genügt es für die Begrenzung des Klirrfaktors auf 1%, die Fourierkoeffizienten $D_{–3}$, ...,$D_3$ zu übertragen. 7.