Exercise 5.9: Selection of OFDM Parameters
In dieser Aufgabe sollen einige OFDM–Parameter eines Mobilfunksystems bestimmt werden. Dabei wird von folgenden Voraussetzungen ausgegangen:
- Die Kohärenzzeit des Kanals ist $T_{\rm coh} = 0.4 \ \rm ms$.
- Die maximale Pfadverzögerung sei $τ_{\rm max} = 25 \ \rm μs$.
- Die Datenrate (Bitrate) beträgt $R_{\rm B} = 1 \ \rm Mbit/s$.
- Alle Unterträger werden 4–QAM–moduliert.
Um eine gewisse Robustheit des Systems gegenüber zeit– und frequenzselektivem Fading zu gewährleisten, muss die folgende Ungleichung erfüllt werden:
- $$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$
Insgesamt soll folgendermaßen vorgegangen werden:
- Vorläufige Festlegung des Guard–Intervalls ($T_{\rm G}'$),
- Bestimmung der optimalen Kernsymboldauer $T$,
- entsprechende Festlegung der Stützstellenzahl der FFT.
Danach ist eventuell eine erneute Bestimmung einiger Systemgrößen aufgrund der bei den Berechnungen vorgenommen Rundungen erforderlich.
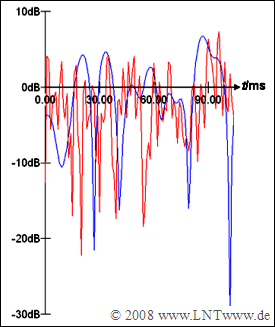
Die Grafik zeigt zwei beispielhafte Dämpfungsverläufe von Mobilfunksystemen in logarithmischer Darstellung.
- Bei der blauen Kurve geschehen die zeitlichen Veränderungen relativ langsam, bei der roten Kurve viermal so schnell.
- Demzufolge weist der blaue Kanal eine viermal größere Kohärenzzeit als der rote Kanal auf.
Hinweise:
- Die Aufgabe gehört zum Kapitel OFDM für 4G–Netze.
- Bezug genommen wird insbesondere auf die Seite Bestimmung einiger OFDM-Parameter.
- Weitere Informationen zum Thema finden Sie im LNTwww–Buch Mobile Kommunikation.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
2. Zur sinnvollen Lösung der Ungleichung aus a) wird das geometrische Mittel verwendet: $$T_{{\rm{opt}}} = \sqrt {T_{\rm{G}} ' \cdot (T_{{\rm{coh}}} - T_{\rm{G}} ')} = \sqrt {{25\,\,{\rm \mu s}} \cdot ({400\,\,{\rm \mu s}} - {25\,\,{\rm \mu s}})} \hspace{0.15cm}\underline { \approx {97\,\,{\rm \mu s}}}.$$
3. Die benötigte Anzahl der Nutzträger ergibt sich als: $$N_{{\rm{Nutz}}} = \left\lceil {\frac{{R_{{\rm{B}}} \cdot (T + T_{\rm{G}} ')}} {{{\rm{log}_2}(M)}}}\right\rceil = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm \mu s}} + {25\,\,{\rm \mu s}} )} {{{\rm{log}_2}(4)}}}\right\rceil\hspace{0.15cm}\underline {= 61}.$$
4. Die Stützstellenzahl der FFT muss eine 2er–Potenz sein. Daraus folgt: $$ N_{{\rm{FFT}}} = 2^{\left\lceil {{\rm{ld}} \hspace{0.05cm}(61 )} \right\rceil } = 2^6\hspace{0.15cm}\underline {= 64}.$$ Ungenutzte Träger können an den Rändern des Spektrums als Guard–Band verwendet werden.
5. $N_G$ ist die gerundete Anzahl der Stützstellen des Guardintervalls. Daraus folgt: $$N_{\rm{G}} = \left\lceil {\frac{{T_{\rm{G}} '}} {{T_{{\rm{opt}}} }} \cdot N_{{\rm{FFT}}} } \right\rceil = \left\lceil {\frac{25\,\,{\rm \mu s}} {97\,\,{\rm \mu s}} \cdot 64 } \right\rceil \hspace{0.15cm}\underline {= 17},$$ $$ T_{\rm{G}} = N_{\rm{G}} \cdot \frac{{T_{{\rm{opt}}} }} {{N_{{\rm{FFT}}} }}= 17 \cdot \frac{{97\,\,{\rm \mu s}}} {64}\hspace{0.15cm}\underline { \approx {26\,\,{\rm \mu s}}}.$$
6. Für die Rahmendauer gilt: $$T_{\rm{R}} = T + T_{\rm{G}} = {97\,\,{\rm \mu s}} + {26\,\,{\rm \mu s}}\hspace{0.15cm}\underline {= {123\,\,{\rm \mu s}}}.$$
7. Mit den Ergebnissen aus d) und e) erhält man: $$ N_{\rm{gesamt}} = N_{\rm{FFT}} + N_{\rm{G}} = 64 + 17 \hspace{0.15cm}\underline {= 81}.$$
8. Die Neuberechnung ist nötig, da sich die Dauer des Guard–Intervalls geändert haben kann. Gegenüber Teilaufgabe c) wird die vorläufige Länge $T_G'$ durch $T_G$ ersetzt: $$N_{{\rm{Nutz}}} = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm \mu s}} + {26\,\,{\rm \mu s}} )} {{{\rm{ld}}(4)}}}\right\rceil = \left\lceil 61.5\right\rceil\hspace{0.15cm}\underline {= 62}.$$