Exercise 4.3: Different Frequencies

Vorgegebene Signalmenge

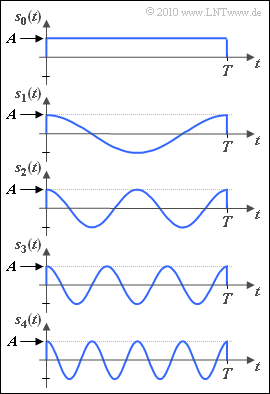
In der Grafik sind $M = 5$ Signale $s_i(t)$ dargestellt. Entgegen der Nomenklatur im Theorieteil sind für die Laufvariable $i$ die $0, \ ... \ , M–$ möglich. Anzumerken ist:

Alle Signale sind zeitbegrenzt auf $0$ bis $T$ ; damit ist auch die Energie aller Signale endlich.
Das Signal $s_1(t)$ hat die Periodendauer $T_0 = T$ . Die Frequenz ist damit gleich $f_0 = 1/T$ .
Die Signale $s_i(t)$ , $i ≠ 0$ , sind Cosinusschwingungen mit der Frequenz $i \cdot f_0$ . Dagegen ist $s_0(t)$ zwischen $0$ und $T$ konstant.
Der Maximalwert aller Signale ist $A$ und es gilt $|s_i(t)| ≤ A$ .

Gesucht sind in dieser Aufgabe die $N$ Basisfunktionen, die hier entgegen der bisherigen Beschreibung im Theorieteil mit $j = 0, \ ... \ , N–1$ durchnummeriert werden.

Hinweis:

Die Aufgabe bezieht sich auf das Kapitel Signale, Basisfunktionen und Vektorräume.

Fragebogen

	$s_i(t) = A \cdot \cos {(2\pi i \cdot t/T)}$ .
	$s_i(t) = A \cdot \cos {(2\pi i \cdot t/T)}$ für $0 ≤ t < T$ , sonst $0$ .
	$s_i(t) = A \cdot \cos {(2\pi t/T \, – \, i \cdot \pi/2)}$ für $0 ≤ t < T$ , sonst $0$ .

$N$ =

	$\varphi_0(t) = s_0(t)$ ,
	$\varphi_0(t) = (1/T)^{\rm 0.5}$ für $0 ≤ t < T$ , außerhalb $0$ .
	$\varphi_0(t) = (2/T)^{\rm 0.5}$ für $0 ≤ t < T$ , außerhalb $0$ .

	$\varphi_1(t) = s_1(t)$ ,
	$\varphi_1(t) = (1/T)^{\rm 0.5} \cdot \cos {(2\pi t/T)}$ für $0 ≤ t < T$ , außerhalb $0$ .
	$\varphi_1(t) = (2/T)^{\rm 0.5} \cdot \cos {(2\pi t/T)}$ für $0 ≤ t < T$ , außerhalb $0$ .

Musterlösung

Solution

(1) Richtig ist der Lösungsvorchlag 2, der die unterschiedlichen Frequenzen und die Begrenzung auf den Bereich

$0 ≤ t < T$ berücksichtigt. Die Signale

$s_i(t)$ gemäß Vorschlag 3 unterscheiden sich dagegen nicht bezüglich der Frequenz, sondern weisen unterschiedliche Phasenlagen auf.

(2) Die energiebegrenzten Signale $s_i(t) = A \cdot \cos {(2\pi i \cdot t/T)}$ sind alle zueinander orthogonal, das heißt, das innere Produkt zweier Signale $s_i(t)$ und $s_k(t)$ mit $i ≠ k$ ist stets $0$ :

$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A^2 \cdot \int_{0}^{T}\cos(2\pi i \cdot t/T) \cdot \cos(2\pi k \cdot t/T)\,{\rm d} t =$

$\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{A^2}{2} \cdot \int_{0}^{T}\cos(2\pi (i-k) t/T) \,{\rm d} t + \frac{A^2}{2} \cdot \int_{0}^{T}\cos(2\pi (i+k) t/T) \,{\rm d} t \hspace{0.05cm}.$

Mit $i ∈ \{0, \ ... \ , 4\}$ und $k ∈ \{0, \ ... \ , 4\}$ sowie $i ≠ j$ ist sowohl $i \, – \, k$ ganzzahlig ungleich $0$ , ebenso die Summe $i + k$ . Dadurch liefern beide Integrale das Ergebnis $0$ :

$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.05cm}\hspace{0.15cm}\underline {N = M = 5} \hspace{0.05cm}.$

(3) Die Energie des innerhalb $T$ konstanten Signals $s_0(t)$ ist gleich

$E_0 = ||s_0(t)||^2 = A^2 \cdot T \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_0(t)|| = A \cdot \sqrt{T}$

$\Rightarrow \hspace{0.3cm} \varphi_0 (t) = \frac{s_0(t)}{||s_0(t)||} = \left\{ \begin{array}{c} 1/\sqrt{T} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$

Richtig ist also der Lösungsvorschlag 2.

(4) Richtig ist hier der letzte Lösungsvorschlag wegen

$E_1 = ||s_1(t)||^2 = \frac{A^2 \cdot T}{2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_1(t)|| = A \cdot \sqrt{{T}/{2}}$

$\Rightarrow \hspace{0.3cm} \varphi_1 (t) = \frac{s_1(t)}{||s_1(t)||} = \left\{ \begin{array}{c} \sqrt{2/T} \cdot \cos(2\pi t/T) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$