Exercise 4.13: Four-level QAM

Signalraumkonstellation der 4–QAM

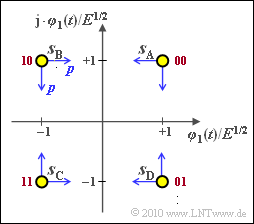
Wir betrachten nun eine Quadraturamplitudenmodulation mit $M = 4$ Symbolen und den (normierten) Signalraumpunkten

$$\boldsymbol{ s}_{\rm A} = (+1, +1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm B} = (-1, +1)\hspace{0.05cm},$$

$$ \boldsymbol{ s}_{\rm C} = (-1, -1)\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm D} = (+1, -1) \hspace{0.05cm}.$$

Die Symbole sind gleichwahrscheinlich. Damit kann man zur Berechnung der mittleren Symbolfehlerwahrscheinlichkeit auf die Mittelung verzichten.

Beispielsweise gilt:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Pr}( \boldsymbol{ s}_{\rm B} \cup \boldsymbol{ s}_{\rm C} \cup \boldsymbol{ s}_{\rm D} \hspace{0.15cm}{\rm entschieden} \hspace{0.05cm}|\hspace{0.05cm} \boldsymbol{ s}_{\rm A}\hspace{0.15cm} {\rm gesendet}) \hspace{0.05cm}.$$

Die Zuordnung der Symbole zu Bitdupeln kann ebenfalls der Grafik (rote Beschriftungen) entnommen werden. Hierbei ist die Graycodierung vorausgesetzt.

Hinweise:

Die Aufgabe bezieht sich auf die Theorieseite 6 von Kapitel 4.4.
Für die Teilaufgabe (4) ist der (zeitdiskrete) AWGN–Kanal mit der Varianz $\sigma_n^2 = N_0/2$ vorausgesetzt.
Für die Wahrscheinlichkeit, dass durch dessen Rauschsignal $n$ ein Symbol horizontal oder vertikal verfälscht wird, gilt mit der komplementären Gaußschen Fehlerfunktion:

$$p = {\rm Pr}( n < -x_0) = {\rm Pr}( n > + x_0) = {\rm Q}(x_0 / \sigma_n) \hspace{0.05cm}.$$

Fragebogen

Musterlösung

Solution

(1) (2) (3) (4) (5)

	correct
	false