Exercise 4.14: 8-PSK and 16-PSK

• Return to book

Signalraumkonstellation der 8–PSK und 16–PSK

Betrachtet wird nun eine Signale $s_i(t)$, die auf den Zeitbereich $0 ≤ t ≤ T$ begrenzt ist. Der Index $i$ durchläuft die Werte $0, \ ... \ , M–1$:

$$s_i(t) = A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) \hspace{0.05cm}.$$

Es handelt sich hierbei um eine Phasenmodulation mit $M$ Signalformen. Man nennt dieses Modulationsverfahren auch M–PSK. $M$ ist meist eine Zweierpotenz.

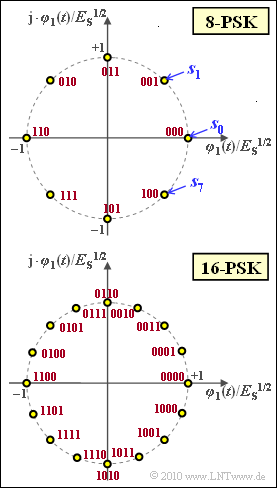
Die Grafik zeigt die Signalraumkonstellation für $M = 8$ (oben) und $M = 16$ (unten). Alle Signalraumpunkte haben gleiche Energie $||\boldsymbol{s}_i||^2 = E_{\rm S}$ („mittlere Symbolenergie”).

Die exakte Berechnung der Fehlerwahrscheinlichkeit ist für $M ≠ 2$ schwierig. Angegeben werden kann dagegen stets die sogenannte Union Bound als obere Schranke für die Symbolfehlerwahrscheinlichkeit ($p_{\rm UB} ≥ p_{\rm S}$):

$$p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) = 2 \cdot {\rm Q} \left (\sqrt{ \frac{ d^2}{ 2 N_0}}\right ) \hspace{0.05cm}.$$

Hierbei bezeichnen:

• $d$ ist der Abstand zwischen zwei benachbarten Punkten, zum Beispiel zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$. Verläuft die Entscheidungsgrenze senkrecht zur Verbindungslinie von $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ genau mittig, so ist $d/2$ der Abstand von $\boldsymbol{s}_0$ bzw. $\boldsymbol{s}_1$ von dieser Entscheidungsgrenze.
• Die Varianz des AWGN–Rauschens ist $\sigma_n^2 = N_0/2$.
• Der Faktor $2$ in obiger Grenze berücksichtigt, dass für $M > 2$ jeder Signalraumpunkt in zwei Richtungen verfälscht werden kann, zum Beispiel bei der 8–PSK das Symbol $\boldsymbol{s}_0$ in das Symbol $\boldsymbol{s}_1$ oder in das Symbol $\boldsymbol{s}_7$.
• ${\rm Q}(x)$ ist die komplementäre Gaußsche Fehlerfunktion, für die folgende Näherung gilt:

$${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

In der letzten Teilaufgabe geht es um die Bitfehlerwahrscheinlichkeit. Für diese wurde im Theorieteil unter der Voraussetzung eines Graycodes folgende Schranke angegeben:

$$p_{\rm B} \le \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$

Diese Gleichung ist allerdings nur für $M > 4$ anzuwenden. Dagegen ergibt sich

• für $M = 2$ aus der Identität mit der BPSK, und
• für $M = 4$ aus der Tatsache, dass die 4–PSK mit der 4–QAM identisch ist,

die exakte Lösung

$$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels Trägerfrequenzen mit kohärenter Demodulation und bezieht sich insbesondere auf die Seite 7.
• Bei der Lösung der Aufgabe können Sie folgende Gleichungen verwenden:

$$\cos(\alpha + \beta) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(\alpha ) \cdot \cos( \beta) - \sin(\alpha ) \cdot \sin( \beta)\hspace{0.05cm}, \hspace{0.25cm} 1 - \cos(2\alpha ) = \sin^2(\alpha )\hspace{0.05cm},$$

$$\int_{0}^{T} \cos^2 ( 2\pi f_{\rm T}t) \,{\rm d} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{0.15cm}{\rm falls}\hspace{0.15cm} f_{\rm T} >> 1/T \hspace{0.05cm}.$$

• Die Zuordnung der 8 bzw. 16 Symbole zu Binärfolgen der Länge 3 bzw. 4 nach der Graycodierung kann der Grafik entnommen werden (rote Beschriftung).

Fragebogen

1

Wie lauten die Basisfunktionen bei der Bandpassdarstellung? $\varphi_1(t)$ und $\varphi_2(t)$ seien jeweils auf den Bereich $0 ≤ t ≤ T$ begrenzt

	$\varphi_1(t) = \cos {(2\pi f_{\rm T}t)}$,
	$\varphi_1(t) = (2/T)^{\rm 1/2} \cdot \cos {(2\pi f_{\rm T}t)}$,
	$\varphi_2(t) = E_{\rm S} \cdot \sin {(2\pi f_{\rm T}t)}$,
	$\varphi_2(t) = \, –(2/T)^{\rm 1/2} \cdot \sin {(2\pi f_{\rm T}t)}.

2

Wie lauten der Inphase– und der Quadraturanteil des Signalraumpunktes $\boldsymbol{s}_i$? Welche Aussagen treffen zu?

	$s_{\rm I \it i} = E_{\rm S}^{\rm 0.5} \cdot \cos {(2\pi \cdot i/M)}$,
	$s_{\rm I \it i} = E_{\rm S}^{\rm 0.5} \cdot \sin {(2\pi \cdot i/M)}$,
	$s_{\rm Q \it i} = E_{\rm S}^{\rm 0.5} \cdot \cos {(2\pi \cdot i/M)}$,
	$s_{\rm Q \it i} = E_{\rm S}^{\rm 0.5} \cdot \sin {(2\pi \cdot i/M)}$.

3

Wie groß ist der Abstand $d$ zwischen zwei benachbarten Signalraumpunkten? Welche Werte ergeben sich für $M = 8$ bzw. $M = 16$?

$M = 8 \text{:} \hspace{0.2cm} d$ = $\ \cdot E_{\rm S}^{\rm 0.5}$

$M = 16 \text{:} \hspace{0.2cm} d$ = $\ \cdot E_{\rm S}^{\rm 0.5}$

4

Welcher Wert ergibt sich für die Union Bound ($p_{\rm UB}$) mit $E_{\rm S}/N_0 = 50$.

$M = 8 \text{:} \hspace{0.2cm} p_{\rm UB}$ = $\ \cdot 10^{\rm –4}$

$M = 16 \text{:} \hspace{0.2cm} p_{\rm UB}$ = $\ \cdot 10^{\rm –2}$

5

Gilt die Aussage: „$p_{\rm UB}$ nähert $p_{\rm S}$ um so genauer an, je größer $M$ ist”?

	JA.
	NEIN.

6

Welche Aussagen gelten hinsichtlich der Bitfehlerwahrscheinlichkeit $p_{\rm UB}$?

	$p_{\rm B}$ ist für $M = 2$ und $M = 4$ am kleinsten.
	$p_{\rm B}$ ist für $M = 8$ am kleinsten.
	$p_{\rm B}$ ist für $M = 16$ am kleinsten.
	$p_{\rm B}$ ist nicht der Hauptgrund, dass man höherstufige PSK einsetzt.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)