Exercise 1.2: A Simple Binary Channel Code

• Return to book

Zur Verdeutlichung der Kanalcodierung

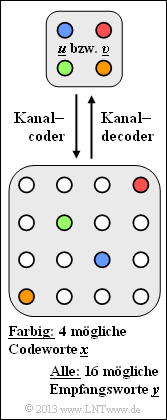
Die Grafik verdeutlicht die hier betrachtete Kanalcodierung C:

• Es gibt vier mögliche Informationsblöcke <>u<u\> = (u_1, u_2, ... , u_k).
• Jeder Informationsblock u wird eindeutig (erkennbar an der gleichen Farbe) dem Codewort x = (x1, x2, ... , xn) zugeordnet.
• Aufgrund von Decodierfehlern (0 → 1, 1 → 0) gibt es mehr als 4, nämlich 16 verschiedene Empfangsworte y = (y1, y2, ... , yn).

Ab Teilaufgabe d) betrachten wir folgende Zuordnung:

Hinweis:

Die hier abgefragten Beschreibungsgrößen wie

• Coderate,
• Hamming–Gewicht,
• Hamming–Distanz, usw.

werden auf Seite 4 und Seite 5 von Kapitel 1.1 definiert.

Fragebogen

1

Aus wievielen Binärsymbolen besteht ein Informationsblock?

$k \ = \ $

2

Wie groß ist die Codewortlänge n?

$n \ = \ $

3

Wie groß ist die Coderate?

$R \ = \ $

4

Ist der hier vorgegebene Code systematisch?

	Ja,
	Nein.

5

Geben Sie die Hamming–Gewichte aller Codeworte an.

$ w_{\rm H} \ (\underline{x}_0) \ = \ $

$ w_{\rm H} \ (\underline{x}_1) \ = \ $

$ w_{\rm H} \ (\underline{x}_2) \ = \ $

$ w_{\rm H} \ (\underline{x}_3) \ = \ $

6

Geben Sie die Hamming–Distanzen zwischen folgenden Codeworten an.

$ d_{\rm H} \ (\underline{x}_0, \underline{x}_1) \ = \ $

$ d_{\rm H} \ (\underline{x}_0, \underline{x}_3) \ = \ $

$ d_{\rm H} \ (\underline{x}_1, \underline{x}_2) \ = \ $

7

Wie groß ist die minimale Hamming–Distanz des betrachteten Codes C?

$ d_{\rm min} \ (C) \ = \ $

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.