Exercise 4.08: Repetition to the Convolutional Codes
Die Turbocodes basieren auf den Faltungscodes, die im Kapitel Grundlagen der Faltungscodierung auführlich behandelt werden.
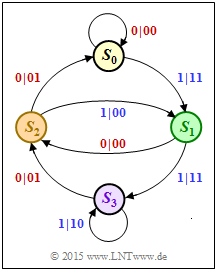
Ausgehend von dem nebenstehenden Zustandsübergangsdiagramm sollen wesentliche Eigenschaften und Kenngrößen des betrachteten Rate–1/2–Faltungscodes ermittelt werden, wobei wir ausdrücklich auf folgende Theorieseiten verweisen:
Systematische Faltungscodes (1)
Darstellung im Zustandsübergangsdiagramm (1)
Definition der freien Distanz (1)
GF(2)–Beschreibungsformen eines Digitalen Filters (2)
Anwendung der $D$–Transformation auf Rate–1/n–Faltungscodes (2)
Im Zustandsübergangsdiagramm wird grundsätzlich vom Zustand $S_0$ ausgegangen. Von jedem Zustand gehen zwei Pfeile ab. Die Beschriftung lautet „$u_i | x_i^{(1)}x_i^{(2)}$”. Bei einem systematischen Code gilt dabei:
- Das erste Codebit ist identisch mit dem Informationsbit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$
- Das zweite Codebit ist das Prüfbit (Paritybit): $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Grundlegendes zu den Turbocodes.
- Ähnliche Aufgaben finden Sie in den Kapiteln 3.1 bis 3.3. In den Fragen zu dieser Aufgabe werden folgende semi–infinite Vektoren verwendet:
- Informationssequenz $\ \underline{u} = (u_1, \, u_2, \, ...)$,
- Paritysequenz $\ \underline{p} = (p_1, \, p_2, \, ...)$,
- Impulsantwort $\ \underline{g} = (g_1, \, g_2, \, ...)$; diese ist gleich der Paritysequenz $\underline{p}$ für $\underline{u} = (1, \, 0, \, 0, \, ...)$.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung