Exercise 2.2Z: Galois Field GF(5)

• Return to book

Additions– und Multiplikationstabelle für $\{a, \, b, \, c, \, d, \, e\}$

Wie in Aufgabe A2.2 betrachten wir einen endlichen Körper der Ordnung $q = 5$ und damit das Galoisfeld

$${\rm GF}(5) = \{{a}, { b},{c},{d},{e}\}\hspace{0.05cm}.$$

Über die Elemente werden weiter keine Aussagen getroffen. Es können sowohl ganze Zahlen sein oder irgendwelche mathematische Ausdrücke. Das Galoisfeld wird ausschließlich bestimmt durch

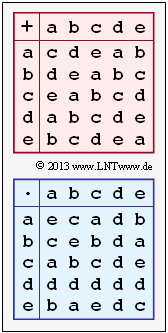
• eine Additionstabelle modulo 5,
• eine Multiplikationstabelle modulo 5,

Die wichtigsten Eigenschaften eines Galoisfeldes sind auf Theorieseite 1 zusammengestellt. In dieser Aufgabe wird Bezug genommen auf

• das Kommutativ– und das Distributivgesetz,
• die neutralen Elemente von Addition und Multiplikation,
• die inversen Elemente von Addition und Multiplikation, sowie
• die Bestimmung primitiver Elemente.

Im vorliegenden Beispiel wäre $\beta$ ein primitives Element, wenn $\beta^2, \ \beta^3$ und $\beta^4$ (allgemein: $\beta^{q-1})$ die übrigen Elemente des Galoisfeldes $\rm GF(5)$ mit Ausnahme des Nullelementes ergeben.

Hinweise:

• Die Aufgabe bezieht ich auf das Themengebiet des Kapitels Einige Grundlagen der Algebra.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Bestimmen Sie das neutrale Element der Addition.

	$N_{\rm A} = a$,
	$N_{\rm A} = b$,
	$N_{\rm A} = c$,
	$N_{\rm A} = d$,
	$N_{\rm A} = e$.

2

Bestimmen Sie das neutrale Element der Multiplikations

	$N_{\rm M} = a$,
	$N_{\rm M} = b$,
	$N_{\rm M} = c$,
	$N_{\rm M} = d$,
	$N_{\rm M} = e$.

3

Ist das Kommutativgesetz erfüllt,

	hinsichtlich Addition, z.B. $a + b = b + a, \ ... \ , \ d + e = e + d$,
	hinstichtlich Multiplikation, z.B. $a \cdot b = b \cdot a, \ ... \ , \ d \cdot e = e \cdot d$.

4

Für welche Ausdrücke ist das Distributivgesetz erfüllt?

	$a \cdot (b + c) = a \cdot b + a \cdot c$,
	$d \cdot (b + c) = d \cdot b + d \cdot c$,
	$e \cdot (a + b) = e \cdot a + e \cdot b$.

5

Ersetzen Sie $a, \ b, \ c, \ d, \ e$ durch Elemente der Zahlenmenge $\{0, \, 1, \, 2, \, 3, \, 4\}$, so dass sich gleiche Operationstabellen ergeben.

$a \ = \ $

$b \ = \ $

$c \ = \ $

$d \ = \ $

$e \ = \ $

6

Welche Aussagen gelten hnsichtlich der inversen Elemente?

	Für alle $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$ gibt es eine additive Inverse.
	Nur für $z_i ∈ \{1, \, 2, \, 3, \, 4\}$ gibt es eine additive Inverse.
	Für alle $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$ gibt es eine multiplikative Inverse.
	Nur für $z_i ∈ \{1, \, 2, \, 3, \, 4\}$ gibt es eine multiplikative Inverse.

7

Welche der Elemente sind primitiv?

	$a = 3$.
	$b = 2$,
	$e = 4$.

Musterlösung

Solution

(1) 

(2) 

(3) 

(4) 

(5) 

(6) 

(7)