Exercise 2.5: Three Variants of GF(2 power 4)

Potenzen zweier Erweiterungskörper über $\rm GF(2^4)$ – nicht ganz vollständig

Irreduzible und primitive Polynome haben große Bedeutung für die Beschreibung von Verfahren zur Fehlerkorrektur. In LN97 findet man zum Beispiel die folgenden irreduziblen Polynome vom Grad $m = 4$:

$p(x) = x^4 + x +1$,
$p(x) = x^4 + x^3 + 1$,
$p(x) = x^4 + x^3 + x^2 + x + 1$.

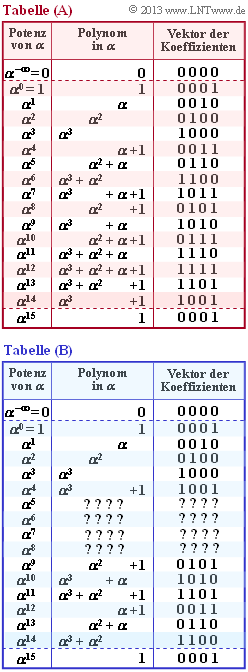
Die beiden ersten Polynome sind auch primitiv. Dies erkennt man aus den Potenztabellen, die rechts angegeben sind – die untere Tabelle (B) allerdings nicht ganz vollständig. Aus beiden Tabellen erkennt man, dass alle Potenzen $\alpha^i$ für $1 ≤ i ≤ 14$ in der Polynomdarstellung ungleich $1$ sind. Erst für $i = 15$ ergibt sich

$$\alpha^{15} = \alpha^{0} = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}{\rm Koeffizientenvektor\hspace{0.15cm} 0001} \hspace{0.05cm}.$$

Nicht angegeben wird, ob sich die rot hinterlegte Tabelle (A) aus dem Polynom $x^4 + x + 1$ oder aus $x^4 + x^3 + 1$ ergibt. Diese Zuordnungen sollen Sie in den Teilaufgaben (1) und (2) treffen. In der Teilaufgabe (3) sollen Sie zudem die fehlenden Potenzen $\alpha^5, \ \alpha^6, \ \alpha^7$ und $\alpha^8$ in der Tabelle (B) ergänzen.

Die Teilaufgabe (4) bezieht sich auf das ebenfalls irreduzible Polynom $p(x) = x^4 + x^3 + x^2 + x +1$. Entsprechend den oben genannten Kriterien sollen Sie entscheiden, ob dieses Polynom primitiv ist oder nicht.

Hinweis:

Die Aufgabe gehört ebenfalls zum Themengebiet des Kapitels Erweiterungskörper.

Fragebogen

Musterlösung

Solution

(1) Aus der oberen Potenztabelle (A) auf der Angabenseite erkennt man unter anderem

$$\alpha^{4} = \alpha + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^{4} + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} p(x) = x^4 + x +1 \hspace{0.05cm}.$$

Richtig ist somit Lösungsvorschlag 1.

(2) Entsprechend der Vorgehensweise in Teilaufgabe (1) kann gezeigt werden, dass Potenztabelle (B) auf dem Polynom $p(x) = x^4 + x^3 + 1$ basiert ⇒ Lösungsvorschlag 2.

(3) Ausgehend von Polynom $p(x) = x^4 + x^3 + 1$ erhält man aus der Bestimmungsgleichung $p(\alpha) = 0$ das Ergebnis $\alpha^4 = \alpha^3 + 1$. Damit ergibt sich weiter:

$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^3 + 1) = \alpha^4 + \alpha = \alpha^3 + \alpha +1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm Vektor\hspace{0.15cm} 1011},$$

$$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^3 +\alpha + 1) = \alpha^4 + \alpha^2 + \alpha= \alpha^3 +\alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm Vektor\hspace{0.15cm} 1111},$$

$$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha^4 +\alpha^3 +\alpha^2 +\alpha = \alpha^2 + \alpha + 1\hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm Vektor\hspace{0.15cm} 0111},$$

$$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot (\alpha^2 + \alpha + 1) = \alpha^3 +\alpha^2 +\alpha \hspace{0.05cm} \Rightarrow\hspace{0.05cm}{\rm Vektor\hspace{0.15cm} 1110}.$$

Right sind somit nur die Lösungsvorschläge 1 und 4. Die beiden anderen Angaben sind vertauscht. Nachfolgend finden Sie die vollständigen Potenztabellen für $p(x) = x^4 + x + 1$ (links, rot hinterlegt) und für $p(x) = x^4 + x^3 + 1$ (rechts, blau hinterlegt).

Zwei Potenztabellen über $\rm GF(2^4)$ für unterschiedliche Polynome

(4) Die beiden Polynome $p(x) = x^4 + x + 1$ und $p(x) = x^4 + x^3 + 1$ sind primitiv. Dies erkennt man daran, dass $\alpha^i$ für $0 < i < 14$ jeweils ungleich $1$ ist. Dagegen gilt $\alpha^{15} = \alpha^0 = 1$. In beiden Fällen kann das Galoisfeld wie folgt ausgedrückt werden:

$${\rm GF}(2^4) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2},\hspace{0.1cm} ... \hspace{0.1cm} , \hspace{0.1cm}\alpha^{14}\hspace{0.1cm}\}\hspace{0.05cm}. $$

Dagegen erhält man für das Polynom $p(x) = x^4 + x^3 + x^2 + x +1$:

$$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^3 + \alpha^2 + \alpha +1\hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm Vektor\hspace{0.15cm} 1111}\hspace{0.05cm},$$

$$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha^4 + \alpha^3 + \alpha^2 + \alpha =$$

$$\ = \ \hspace{-0.15cm} (\alpha^3 + \alpha^2 + \alpha +1) + \alpha^3 + \alpha^2 + \alpha = 1 \hspace{0.25cm} \Rightarrow\hspace{0.25cm}{\rm Vektor\hspace{0.15cm} 0001}\hspace{0.05cm}.$$

Hier ist also bereits $\alpha^5 = \alpha^0 = 1 \ \Rightarrow \ p(x)$ ist kein primitives Polynom ⇒ Lösungsvorschlag 2. Für die weiteren Potenzen gilt für dieses Polynom:

$$\alpha^6 = \alpha^{11} = \alpha\hspace{0.05cm},\hspace{0.2cm} \alpha^7 = \alpha^{12} = \alpha^2\hspace{0.05cm},\hspace{0.2cm} \alpha^8 = \alpha^{13} = \alpha^3\hspace{0.05cm},$$

$$\alpha^9 = \alpha^{14} = \alpha^4\hspace{0.05cm},\hspace{0.2cm} \alpha^{10} = \alpha^{15} = \alpha^0 = 1\hspace{0.05cm}.$$

	$\alpha^5 = \alpha^3 + \alpha + 1 \ \Rightarrow \ \rm Koeffizientenvektor „1011”$,
	$\alpha^6 = \alpha^2 + 1 \ \Rightarrow \ \rm Koeffizientenvektor „0111”$,
	$\alpha^7 = \alpha^3 + \alpha^2 + \alpha + 1 \ \Rightarrow \ \rm Koeffizientenvektor „1111”$,
	$\alpha^8 = \alpha^3 + \alpha^2 + \alpha \ \Rightarrow \ \rm Koeffizientenvektor „1110”$.

	Ja.
	Nein.