Exercise 1.16Z: Bounds for the Gaussian Error Function

Die Wahrscheinlichkeit, dass eine Gaußsche Zufallsgröße $n$ mit Streuung $\sigma$ → Varianz $\sigma^2$ betragsmäßig größer ist als ein Wert $A$, ist gleich

$${\rm Pr}(n > A) = {\rm Pr}(n < -A) ={\rm Q}(A/\sigma) \hspace{0.05cm}.$$

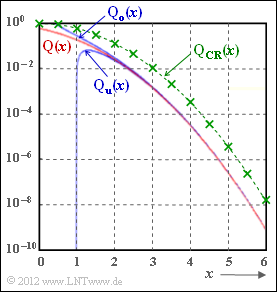
Hierbei verwendet ist eine der wichtigsten Funktionen für die Nachrichtentechnik (in der Grafik rot eingezeichnet): die Komplementäre Gaußsche Fehlerfunktion

$$\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int\limits_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.$$

${\rm Q}(x)$ ist eine monoton fallende Funktion mit ${\rm Q}(0) = 0.5$. Für große Werte von $x$ tendiert ${\rm Q}(x)$ gegen Null.

Das Integral der Q–Funktion ist analytisch nicht lösbar und wird meist in Tabellenform angegeben. Aus der Literatur bekannt sind aber handhabbare Näherungslösungen bzw. Schranken für positive $x$–Werte:

die obere Schranke (obere blaue Kurve in nebenstehender Grafik, nur gültig für $x > 0$):

$$ \rm Q_o(\it x)=\frac{\rm 1}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-\it x^{\rm 2}/\rm 2}\hspace{0.15cm} \ge \hspace{0.15cm} \rm Q (\it x) \hspace{0.05cm},$$

die untere Schranke (untere blaue Kurve in der Grafik, nur gültig für $x > 1$):

$$ \rm Q_u(\it x)=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-\it x^{\rm 2}/\rm 2} \hspace{0.15cm} \le \hspace{0.15cm} \rm Q (\it x) \hspace{0.05cm},$$

die Chernoff–Rubin–Schranke (grüne Kurve in der Grafik, gezeichnet für $K = 1$):

$$\rm Q_{CR}(\it x)=K \cdot \rm e^{-\it x^{\rm 2}/\rm 2} \hspace{0.15cm} \ge \hspace{0.15cm} \rm Q (\it x) \hspace{0.05cm}.$$

In der Aufgabe ist zu untersuchen, in wie weit diese Schranken als Näherungen für ${\rm Q}(x)$ herangezogen werden können und welche Verfälschungen sich dadurch ergeben.

Hinweis:

Die Aufgabe bezieht sich auf das Kapitel Schranken für die Blockfehlerwahrscheinlichkeit dieses Buches sowie auf das Kapitel Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken im Buch „Stochastische Signaltheorie”. Die Aufgabe bietet auch einige wichtige Hinweise zur Lösung der Aufgabe 1.16, in der die Funktion ${\rm Q}_{\rm CR}(x)$ zur Herleitung der Bhattacharyya–Schranke für den AWGN–Kanal benötigt wird. Weiter verweisen wir auf das folgende Interaktionsmodul:

Komplementäre Gaußsche Fehlerfunktion

Fragebogen

$\ {\rm Q}_{o}(x = 4)$ =

$\ \cdot 10^{-5} $

$\ {\rm Q}_{u}(x = 4)$ =

$\ \cdot 10^{-5} $

	Für $x ≥ 2$ sind die beiden Schranken brauchbar.
	Für $x < 1$ ist ${\rm Q}_{u}(x)$ unbrauchbar (wegen ${\rm Q}_{u}(x) < 0$).
	Für $x < 1$ ist ${\rm Q}_{o}(x)$ unbrauchbar (wegen ${\rm Q}_{o}(x) > 1$).

$\ {\rm Q}_{\rm CR}(x)/{\rm Q}_{o}(x) \ : \ \ \ x =2$ =

$\ x =4$ =

$\ x =6$ =

$\ K$ =

Musterlösung

Solution

(1) Die obere Schranke lautet:

$${\rm Q_o}(x)=\frac{1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_o}(4 )=\frac{1}{\sqrt{\rm 2\pi}\cdot 4}\cdot {\rm e}^{-8 }\hspace{0.15cm}\underline{\approx 3.346 \cdot 10^{-5}}\hspace{0.05cm}.$$

Die untere Schranke kann wie folgt umgewandelt werden:

$${\rm Q_u}( x)=(1-1/x^2) \cdot {\rm Q_o}(x) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_u}(4 ) \hspace{0.15cm}\underline{\approx 3.137 \cdot 10^{-5}} \hspace{0.05cm}.$$

Die relativen Abweichungen gegenüber dem „echten” Wert ${\rm Q}(4) = 3.167 · 10^{–5}$ sind $+5%$ bzw. $–1%.$

(2) Richtig sind Antwort 1 und 2. Für $x = 2$ wird der tatsächliche Funktionswert ${\rm Q}(x) = 2.275 · 10^{–2}$ begrenzt durch ${\rm Q}_{o}(x) = 2.7 · 10^{–2}$ bzw. ${\rm Q}_{u}(x) = 2.025 · 10^{–2}$. Die relativen Abweichungen betragen $18.7%$ bzw. $–11%.$ Die letzte Aussage ist falsch. Erst für $x < 0.37$ gilt ${\rm Q}_{o}(x) > 1.$

(3) Für den Quotienten aus ${\rm Q}_{\rm CR}(x)$ und ${\rm Q}_{o}(x)$ gilt nach den vorgegebenen Gleichungen:

$$q(x) = \frac{{\rm Q_{CR}}(x)}{{\rm Q_{o}}(x)} = \frac{{\rm exp}(-x^2/2)}{{\rm exp}(-x^2/2)/({\sqrt{2\pi} \cdot x})} = {\sqrt{2\pi} \cdot x}$$

$$\Rightarrow \hspace{0.3cm} q(x) \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} q(x =2) = 5\hspace{0.05cm}, \hspace{0.2cm}q(x =4) = 10\hspace{0.05cm}, \hspace{0.2cm}q(x =6) = 15\hspace{0.05cm}.$$

Je größer der Abszissenwert x, um so ungenauer wird ${\rm Q}(x)$ durch ${\rm Q}_{\rm CR}(x)$ angenähert. Bei Betrachtung der Grafik auf der Angabenseite hat man (hatte ich) den Eindruck, dass ${\rm Q}_{\rm CR}(x)$ sich aus ${\rm Q}(x)$ durch Verschieben nach unten bzw. Verschieben nach oben ergibt. Das ist aber nur eine optische Täuschung und entspricht nicht dem Sachverhalt.

(4) Mit K = 0.5 stimmt die neue Schranke $0.5 · {\rm Q}_{\rm CR}(x)$ für $x = 0$ exakt mit ${\rm Q}(x=0) = 0.500$ überein. Für größere Abszissenwerte wird damit auch die Verfälschung $q = 1.25 · x$ nur halb so groß.