Exercise 1.12: Hard Decision vs. Soft Decision
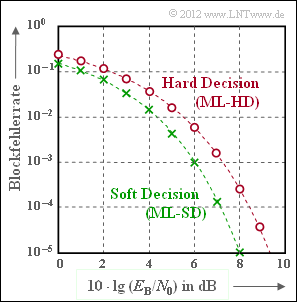
Die Abbildung zeigt die Blockfehlerwahrscheinlichkeit für den $(7, \, 4, \, 3)$–Hamming–Code, wobei für den Empfänger zwei Varianten berücksichtigt sind:
- Bei Maximum–Likelihood–Detektion mit harten Entscheidungen (Hard Decision, HD), die im vorliegenden Fall (perfekter Code) auch durch Syndromdecodierung realisiert werden kann, ergibt sich die rote Kurve (mit Kreismarkierung).
- Der Kanal kann bei „Hard Decision” vereinfacht durch das BSC–Modell ersetzt werden. Der Zusammenhang zwischen dem BSC–Parameter $\varepsilon$ und dem AWGN–Quotienten $E_{\rm B}/N_{0}$ (in der Grafik verwendet) ist wie folgt gegeben:
- $$\varepsilon = {\rm Q}\left ( \sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \right ) \hspace{0.05cm}.$$
- Hier bezeichnet ${\rm Q}(x)$ die komplementäre Gaußsche Fehlerfunktion und $R$ die Coderate.
- Die grüne Kurve (mit Kreuzen) zeigt die Blockfehlerwahrscheinlichkeit bei „weichen” Entscheidungen (Soft Decision, SD). Dieser Funktionsverlauf lässt sich nicht in geschlossen–mathematischer Form angeben. Die in der Grafik eingezeichnete Kurve ist eine in [Fri96] angegebene obere Schranke:
- $$ {\rm Pr(Blockfehler)} \hspace{-0.15cm}\ \le \ \hspace{-0.15cm} 7 \cdot {\rm Q}\left ( \sqrt{ 3 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right )+7 \cdot {\rm Q}\left ( \sqrt{ 4 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right ) + {\rm Q}\left ( \sqrt{ 7 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right ) \hspace{0.05cm}.$$
- Der jeweils erste Faktor im Argument der$\rm Q$–Funktion gibt die möglichen Hamming–Distanzen an: $i = 3, \, 4$ und $7$.
- Die Vorfaktoren berücksichtigen die Vielfachheiten $W_{3} = W_{4} = 7$ und $W_{7} = 1$, und $R = 4/7$ beschreibt die Coderate.
- Für $10 · \lg {E_{\rm B}/N_0} > 8 \ \rm dB$ ist $\rm Pr(Blockfehler) < 10^{–5}$.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Decodierung linearer Blockcodes.
- Die oben zitierte Literaturstelle [Fri96] verweist auf das Buch „Friedrichs, B.: Kanalcodierung – Grundlagen und Anwendungen in modernen Kommunikations- systemen. Berlin – Heidelberg: Springer, 1996”.
- Verwenden Sie für numerische Ergebnisse das Berechnungsmodul Komplementäre Gaußsche Fehlerfunktionen.
- Für die Teilaufgaben (1) bis (4) wird stets von Hard Decision ausgegangen.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- $${\rm Pr(Blockfehler)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm Pr(kein\hspace{0.15cm} Blockfehler)} - {\rm Pr(ein\hspace{0.15cm} Blockfehler)} = $$
- $$\hspace{2.875cm}\ = \ \hspace{-0.15cm}1 - (1 - \varepsilon)^7 - 7 \cdot \varepsilon \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$
- $$\varepsilon = 0.01:\hspace{0.2cm} {\rm Pr(Blockfehler)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - 0.99^7 - 7 \cdot 0.01 \cdot 0.99^6= $$
- $$\hspace{0.1cm}\ = \ \hspace{-0.15cm} 1 - 0.932065 - 0.065904\hspace{0.15cm}\underline{\approx 2.03 \cdot 10^{-3}}\hspace{0.05cm},$$
- $$\varepsilon = 0.001:\hspace{0.2cm} {\rm Pr(Blockfehler)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - 0.999^7 - 7 \cdot 0.001 \cdot 0.999^6= $$
- $$\hspace{0.1cm}\ = \ \hspace{-0.15cm} 1 - 0.993021 - 0.006958\hspace{0.15cm}\underline{\approx 2.09 \cdot 10^{-5}}\hspace{0.05cm}.$$
(2) Ein jeder $(n, \, k, \, 3)$ Hamming–Code kann nur einen Bitfehler korrigieren. Damit gilt allgemein für den BSC–Kanal mit der Codewortlänge $n$:
- $${\rm Pr(Blockfehler)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - (1 - \varepsilon)^n - n \cdot \varepsilon \cdot (1 - \varepsilon)^{n-1}=$$
- $$\hspace{2.875cm}\ = \ \hspace{-0.15cm} 1 - \left [ 1 - {n \choose 1}\cdot \varepsilon + {n \choose 2}\cdot \varepsilon^2 - \hspace{0.05cm}... \hspace{0.05cm} \right ] -$$
- $$\hspace{3.1cm}\ . \ \hspace{0.18cm} - \left [ n \cdot \varepsilon \cdot \left ( 1 - {{n-1} \choose 1}\cdot \varepsilon + {{n-1} \choose 2}\cdot \varepsilon^2 - \hspace{0.05cm}... \hspace{0.05cm}\right ) \right ] \hspace{0.05cm}.$$
Bei Vernachlässigung aller Terme mit $\varepsilon^3, \ \varepsilon^4, \ ...$ erhält man:
- $${\rm Pr(Blockfehler)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} n \cdot \varepsilon - {n \choose 2}\cdot \varepsilon^2 - n \cdot \varepsilon + n \cdot \varepsilon {{n-1} \choose 1}\cdot \varepsilon + \hspace{0.05cm}... \hspace{0.05cm} =$$
- $$\hspace{2.875cm}\ = \ \hspace{-0.15cm} -1/2 \cdot n \cdot (n-1)\cdot \varepsilon^2 + n \cdot (n-1)\cdot \varepsilon^2 = n \cdot (n-1)/2 \cdot \varepsilon^2 \hspace{0.05cm}.$$
⇒ Richtig ist Lösungsvorschlag 1. Für den $(7, \, 4, \, 3)$–Hamming–Code ergibt sich somit:
- $${\rm Pr(Blockfehler)} \le \left\{ \begin{array}{c} 2.1 \cdot 10^{-3}\\ 2.1 \cdot 10^{-5} \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} \varepsilon = 10^{-2} \\ {\rm f\ddot{u}r}\hspace{0.15cm} \varepsilon = 10^{-3} \\ \end{array} \hspace{0.05cm}.$$
Durch Vergleich mit dem Ergebnis der Teilaufgabe (1) erkennt man die Gültigkeit dieser Näherung. Diese ist um so besser, je kleiner die BSC–Verfälschungswahrscheinlichkeit $\varepsilon$ ist.
(3) Die Ergebnisse der Teilaufgabe 2) lassen sich wie folgt zusammenfassen:
- $${\rm Pr(Blockfehler)} = \left\{ \begin{array}{l} 3 \cdot \varepsilon^2 \\ 21 \cdot \varepsilon^2\\ 105 \cdot \varepsilon^2\\ \end{array} \right.\quad \begin{array}{*{1}l} {\rm f\ddot{u}r}\hspace{0.15cm} n = 3 \\ {\rm f\ddot{u}r}\hspace{0.15cm} n = 7 \\ {\rm f\ddot{u}r}\hspace{0.15cm} n = 15 \\ \end{array} \hspace{0.05cm}.$$
Richtig ist Antwort 1. Die geringste Blockfehlerwahrscheinlichkeit besitzt natürlich der Hamming–Code mit der geringsten Rate $R = 1/3$, also mit der größten relativen Redundanz.
(4) Bei Hard Decision gilt mit der komplementären Gaußschen Fehlerfunktion ${\rm Q}(x)$:
- $$\varepsilon = {\rm Q}\left ( \sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \right )\hspace{0.3cm} \Rightarrow \hspace{0.3cm} E_{\rm B}/N_0 = \frac{[{\rm Q}^{-1}(\varepsilon)]^2}{2R}$$
- $$ \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 20 \cdot {\rm lg} \hspace{0.1cm}[{\rm Q}^{-1}(\varepsilon)] - 10 \cdot {\rm lg} \hspace{0.1cm} (2R) \hspace{0.05cm}.$$
Daraus erhält man mit $\varepsilon = 0.01 \ ⇒ \ {\rm Q}^{–1}(\varepsilon) = 2.33$:
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 20 \cdot {\rm lg} \hspace{0.1cm}(2.33) - 10 \cdot {\rm lg} \hspace{0.1cm} (8/7) = 7.35\,{\rm dB} - 0.58\,{\rm dB}\hspace{0.15cm}\underline{\approx 6.77\,{\rm dB}}\hspace{0.05cm}.$$
In analoger Weise ergibt sich für $\varepsilon = 0.001 \ ⇒ \ {\rm Q}^{–1}(\varepsilon) ≈ 3.09$.
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 20 \cdot {\rm lg} \hspace{0.1cm}(3.09) - 0.58\,{\rm dB}\hspace{0.15cm}\underline{\approx 9.22\,{\rm dB}}\hspace{0.05cm}.$$
(5) Wir beziehen uns auf die Blockfehlerwahrscheinlichkeit $10^{–5}$. Nach dem Ergebnis der Teilaufgabe (2) darf dann die BSC–Verfälschungswahrscheinlichkeit nicht größer sein als
- $$\varepsilon = \sqrt{\frac{10^{-5}}{21}} = 6.9 \cdot 10^{-4} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q}^{-1}(\varepsilon) = 3.2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 9.52\,{\rm dB}\hspace{0.05cm}.$$
Mit Soft Decision genügen laut Angabe $8 \ {\rm dB} \ ⇒ \ 10 · \lg {G_{\rm SD}} \ \underline{= 1.52 \ {\rm dB}}$.