Exercise 2.4: DSL/DMT with IDFT/DFT
Eine Realisierungsform des DMT–Verfahrens (steht für Discrete Multitone Transmission) basiert auf der Inversen Diskreten Fouriertransformation (IDFT) beim Sender sowie der Diskreten Fouriertransformation (DFT) am Empfänger.
Beim Sender werden $N/2–1$ Nutzer durch die komplexen Spektralkoeffizienten $D_{k} (k = 1,$ ... , $N/2–1)$ den Frequenzen $f_{k} = k \cdot f_{0}$ zugewiesen. Die Grundfrequenz $f_{0}$ ist der Kehrwert der Symboldauer $T$.
Es gilt $D_{k} \in \{ ±1 ± {\rm j} \}$, falls ein Kanal belegt ist, im anderen Fall ist $D_{k} = 0$. Die Koeffizienten $D_{0}$ und $D_{N/2}$ sind stets Null. Die obersten Koeffizienten werden konjugiert–komplex belegt:
- $$D_k = D_{N-k}^{\star},\hspace{0.2cm}k = N/2 +1,\hspace{0.05cm} \text{...} \hspace{0.05cm}, N-1 \hspace{0.05cm}.$$
Dadurch wird sicher gestellt, dass das Zeitsignal $s(t)$ stets reell ist. Die Abtastwerte $s_{0}$, ... , $s_{N–1}$ dieses Signals werden dabei durch die IDFT gebildet, wobei der zeitliche Abstand zweier Abtastwerte
- $$\Delta t = T/N = 1/(N \cdot f_{0})$$
beträgt. Durch Tiefpassfilterung erhält man das zeitkontinuierliche Signal.
Bei ADSL/DMT gilt $N = 512$ und $f_{0} = 4.3125 \ \rm kHz$. In dem hier betrachteten Beispiel seien die Parameter zur Vereinfachung wie folgt angenommen:
- $$N = 16,\hspace{0.2cm}\Delta t = 10\,{\rm µ s} \hspace{0.05cm}.$$
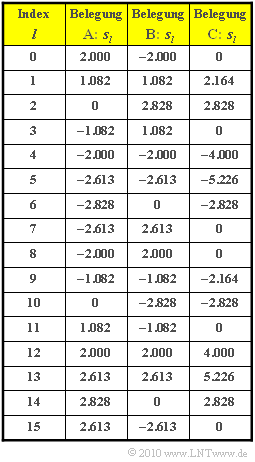
In der obigen Tabelle sind für drei verschiedene $D_{k}$–Belegungen die Abtastwerte $s_{l} (l = 0$, ... , $15)$ nach der IDFT angegeben. Gesucht sind die zugehörigen Spektralkoeffizienten $D_{k} (k = 0$, ... , $15).$
Hinweise:
- Die Aufgabe gehört zum Kapitel xDSL als Übertragungstechnik.
- Das Sendesignal hat bei DSL die Form
- $$s(t) = \sum_{k = 1}^{K} \left [ 2 \cdot {\rm Re}\{D_k\} \cdot \cos(2\pi \cdot k f_0 \cdot t ) - 2 \cdot {\rm Im}\{D_k\} \cdot \sin(2\pi \cdot k f_0 \cdot t )\right ] \hspace{0.05cm}.$$
- Beachten Sie auch die folgende trigonometrische Beziehung:
- $$\cos(2\pi f_0 t + \phi_0) = \cos( \phi_0) \cdot \cos(2\pi f_0 t ) - \sin( \phi_0) \cdot \sin(2\pi f_0 t ) \hspace{0.05cm}.$$
- Man bezeichnet als den Crestfaktor (oder den Scheitelfaktor) eines Signals das Verhältnis von Maximalwert und Effektivwert.
- Sie können Ihre Lösung mit dem interaktiven Applet Diskrete Fouriertransformation überprüfen.
Fragebogen
Musterlösung
(2) Die Rahmendauer $T$ ergibt sich zu $N \cdot \Delta t = 0.16 \rm ms$. Die Grundfrequenz ist hier dementsprechend $f_{0} = 1/T = 6.25 \ \rm kHz$ und die Gesamtbandbreite beträgt $B = 8 \cdot f_{0} = 50 \ \rm kHz$. Zum Vergleich: Bei ADSL ergibt sich diese Bandbreite zu $256 \cdot 4.3125 \ \rm kHz\ \underline{= 1104 \ kHz}.$
(3) Richtig ist der zweite Lösungsvorschlag. Aus den $16$ Abtastwerten $s_{l}$ in der ersten Spalte der Tabelle erkennt man, dass $s(t)$ eine harmonische Schwingung mit der Periodendauer $T_{0} = T$ beschreibt (nur eine Schwingung). Die Amplitude ist gleich $2.828$ (zweimal Wurzel aus 2) und die Phase beträgt $\phi_0 = 45° \ (π/4)$. Damit kann für das zeitkontinuierliche Signal geschrieben werden (mit $f_{0} = 1/T$):
- $$s(t) = 2 \cdot \sqrt{2}\cdot \cos(2\pi f_0 t + \pi /4) \hspace{0.05cm}.$$
Mit der angegebenen trigonometrischen Umformung und ${\rm cos} \ (π/4) \ = \ {\rm sin} \ (π/4) \ = \ 2^{–0.5}$ gilt weiterhin:
- $$s(t) = 2 \cdot \cos(2\pi f_0 t ) - 2 \cdot \sin(2\pi f_0 t ) \hspace{0.05cm}.$$
Ein Koeffizientenvergleich mit der weiteren Gleichung
- $$s(t) = \sum_{k = 1}^{K} \left [ 2 \cdot {\rm Re}\{D_k\} \cdot \cos(2\pi \cdot k f_0 \cdot t ) - 2 \cdot {\rm Im}\{D_k\} \cdot \sin(2\pi \cdot k f_0 \cdot t )\right ] \hspace{0.05cm}$$
liefert das Ergebnis:
- $$2 \cdot {\rm Re}\{D_1\} = 2 \hspace{0.3cm} \ \Rightarrow \ \hspace{0.3cm} {\rm Re}\{D_1\} = 1\hspace{0.05cm},$$
- $$2 \cdot {\rm Im}\{D_1\} = 2 \hspace{0.3cm} \ \Rightarrow \ \hspace{0.3cm} {\rm Im}\{D_1\} = 1\hspace{0.05cm}.$$
Weiterhin ist zu beachten, dass der Koeffizient $D_{15}$ mit dem konjugiert–komplexen Wert zu belegen ist:
- $$D_{15} = D_{1}^{\star} = 1 - {\rm j}\hspace{0.05cm}.$$
Zum gleichen Ergebnis wäre man durch Auswertung der (zeitkontinuierlichen) Fouriertransformierten von $s(t)$ gekommen:
- $$S(f) = (1 + {\rm j}) \cdot \delta (f - f_0) + (1 - {\rm j}) \cdot \delta (f + f_0)\hspace{0.05cm}.$$
Der Koeffizient $D_1$ beschreibt das Gewicht bei der ersten Diracfunktion (also bei $f = f_0$), der Koeffizient $D_{15} = D_{–1}$ das Gewicht der Diracfunktion bei $f = –f_0$. Hierbei ist die implizite periodische Fortsetzung bei der DFT (bzw. IDFT) zu beachten.
(4) Zeichnet man sich die Abtastwerte $s_l$ auf, so erkennt man nun die 3–fache Frequenz. Unter anderem aus dem Vergleich von $s_2$ und $s_10$ ergibt sich:
- $$8 \cdot \Delta t = \frac{T}{2} = 1.5 \cdot T_0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T_0 = \frac{T}{3}\hspace{0.05cm}.$$
Die Amplitude ist gegenüber der Belegung $A$ unverändert. Die Phase $\phi_0$ erkennt man aus dem ersten Maximum bei $l = 2$:
- $$ s(t) \ = \ 2 \cdot \sqrt{2}\cdot \cos(2\pi \cdot 3 f_0 \cdot ( t - 2 \cdot \Delta t)) = $$
- $$ \hspace{0.85cm} = \ 2 \cdot \sqrt{2}\cdot \cos(2\pi \cdot 3 f_0 \cdot t + \phi_0), \hspace{0.3cm} \phi_0 = 12 \pi \cdot \frac{\Delta t}{T} = \frac{3 \pi}{4} \hspace{0.05cm}.$$
Nach gleicher Vorgehensweise wie bei Aufgabe 3) erhält man nun mit $ {\rm cos}(3π/4) \ = \ sin(3π/4) = –2^{–0.5}$:
- $${\rm Re}\{D_3\} = -1, \hspace{0.2cm} {\rm Im}\{D_3\} = -1\hspace{0.05cm}.$$
Richtig ist somit der Lösungsvorschlag 3, wobei wieder $D_{13} = D_{3}^∗$ zu berücksichtigen ist.
(5) Richtig ist hier der erste Lösungsvorschlag. Aufgrund der Linearität der IDFT ergeben sich die Koeffizienten $D_1, D_3, D_{13}$ und $D_{15}$ entsprechend den Ergebnissen von 5) und 4).
(6) Die Belegung $\boldsymbol{\rm C}$ führt zu der Summe zweier harmonischer Schwingungen (mit $f_0$ bzw. $3f_0$), jeweils mit gleicher Amplitude $A$. Somit ergibt sich für die mittlere Signalleistung:
- $$P_{\rm S} = 2 \cdot \frac{A^2}{2} = A^2 = 8\hspace{0.05cm}.$$
Der Effektivwert ist gleich der Wurzel aus der Sendeleistung $P_{\rm S}$:
- $$s_{\rm eff} = \sqrt{P_{\rm S}} = A = 2.828\hspace{0.05cm}.$$
Der Maximalwert ist aus der Tabelle ablesbar:
- $$s_{\rm max} = 5.226\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm CF} = \frac{5.226}{2.828} \hspace{0.15cm} \underline{\approx 1.85 \hspace{0.05cm}}.$$
Dagegen würde bei den beiden Belegungen $\boldsymbol{\rm A}$ und $\boldsymbol{\rm B}$ jeweils ${\rm CF} = 2^{0.5} = 1.414$ gelten.