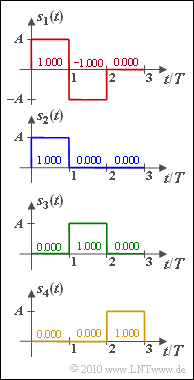
Exercise 4.1: About the Gram-Schmidt Process

• Return to book

Vorgabe zum Gram-Schmidt-Verfahren

Für die vier durch die Abbildung definierten Signale $s_1(t), \, ... \, , s_4(t)$ sind durch Anwendung des Gram–Schmidt–Verfahrens die drei sich ergebenden Basisfunktionen $\varphi_1(t)$, $\varphi_2(t)$ und $\varphi_3(t)$ zu ermitteln, so dass für die Signale mit $i = 1, \, ... \, , 4$ geschrieben werden kann:

$$s_i(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + s_{i3} \cdot \varphi_3(t)\hspace{0.05cm}.$$

In der Teilaufgabe (1) gelte $A^2 = 1 \ \rm mW$ und $T = 1 \ \rm \mu s$. In den späteren Teilaufgaben sind die Amplitude und die Zeit jeweils normierte Größen: $A = 1$, $T = 1$. Damit sind sowohl die Koeffizienten $s_{\it ij}$ als auch die Basisfunktionen $\varphi_{\it}(t)$ – jeweils mit $j = 1, 2, 3$ – dimensionslose Größen.

Hinweise:

• Die Aufgabe gehört zum Kapitel Signale, Basisfunktionen und Vektorräume.
• Bezug genommen wird insbesondere auf die Seiten Orthonormale Basisfunktionen und Gram–Schmidt–Verfahren.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche Einheiten besitzen die folgenden Größen mit $A^2 = 1 \, \rm mW$ und $T = 1 \, {\rm \mu s}$?

	Die Basisfunktionen $\varphi_j(t)$ sind dimensionslos.
	Die Basisfunktionen $\varphi_j(t)$ haben die Einheit $\rm \sqrt{\rm s}$.
	Die Koeffizienten $s_{\it ij}$ sind dimensionslos.
	Die Koeffizienten $s_{\it ij}$ haben die Einheit $\rm \sqrt{\rm Ws}$.

2

Führen Sie den ersten Schritt des Gram–Schmidt–Verfahrens durch. Wie für die weiteren Aufgaben gelte $A = 1$ und $T = 1$.

$s_{\rm 11} \ = \ $

$s_{\rm 12} \ = \ $

$s_{\rm 13} \ = \ $

3

Wie lauten die Koeffizienten des Signals $s_2(t)$ mit $A = 1$ und $T = 1$?

$s_{\rm 21} \ = \ $

$s_{\rm 22} \ = \ $

$s_{\rm 23} \ = \ $

4

Wie lauten die Koeffizienten des Signals $s_3(t)$ mit $A = 1$ und $T = 1$?

$s_{\rm 31} \ = \ $

$s_{\rm 32} \ = \ $

$s_{\rm 33} \ = \ $

5

Wie lauten die Koeffizienten des Signals $s_4(t)$ mit $A = 1$ und $T = 1$?

$s_{\rm 41} \ = \ $

$s_{\rm 42} \ = \ $

$s_{\rm 43} \ = \ $

Musterlösung

Solution

(1)  Richtig sind die Lösungsvorschläge 2 und 4:

• Jede orthonormale Basisfunktion soll die Energie 1 aufweisen, das heißt, es muss gelten:

$$||\varphi_j(t)||^2 = \int_{-\infty}^{+\infty}\varphi_j(t)^2\,{\rm d} t = 1 \hspace{0.05cm}.$$

• Damit diese Bedingung zu erfüllen ist, muss die Basisfunktion die Einheit $\rm \sqrt{\rm s}$ besitzen. Zu berücksichtigen ist noch die Gleichung

$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t).$$

• Die Signale selbst weisen wie $A$ die Einheit $\rm \sqrt{\rm W}$ auf. Wegen der Einheit $\rm \sqrt{\rm 1/s}$ von $\varphi_{ j}(t)$ ist diese Gleichung nur dann mit der richtigen Dimension zu erfüllen, wenn die Koeffizienten $s_{\it ij}$ mit der Einheit $\rm \sqrt{\rm Ws}$ angegeben werden.

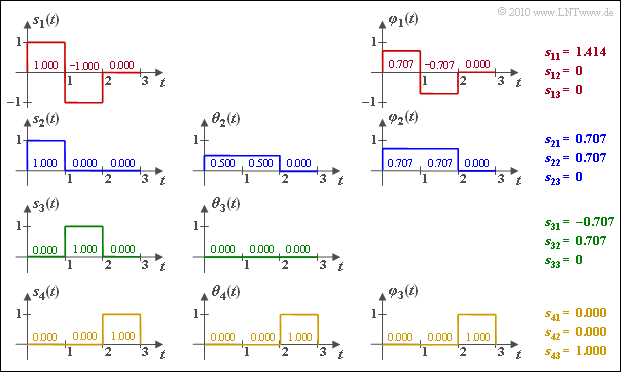
(2)  Die Energie des Signals $s_1(t)$ ist gleich $E_1 = 2$. Daraus folgt für die Norm, die Basisfunktion $\varphi_1(t)$ und den Koeffizienten $s_{\rm 11}$:

$$||s_1(t)|| = \sqrt{2},\hspace{0.2cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.2cm} s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } \hspace{0.05cm}.$$

Die weiteren Koeffizienten sind $\underline {s_{\rm 12} = s_{\rm 13} = 0}$, da die zugehörigen Basisfunktionen bisher noch gar nicht gefunden wurden, während $\varphi_1(t)$ formgleich mit $s_1(t)$ ist.

(3)  Da nach Berücksichtigung von $s_2(t)$ höchstens zwei Basisfunktionen gefunden sind, gilt mit Sicherheit $s_{\rm 23} \hspace{0.15cm} \underline{= 0}$. Dagegen erhält man für den Koeffizienten

$$||s_1(t)|| = \sqrt{2},\hspace{0.2cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.2cm} s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } \hspace{0.05cm}.$$

für die Hilfsfunktion $\theta_2(t)$:

$$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = \left\{ \begin{array}{c} 1 - 0.707 \cdot 0.707 = 0.5\\ 0 - 0.707 \cdot (-0.707) = 0.5 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < 1 \\ 1 \le t < 2 \\ \end{array} \hspace{0.05cm},$$

für die zweite Basisfunktion:

$$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||},\hspace{0.2cm} ||\theta_2(t)|| = \sqrt{0.5^2 + 0.5^2} = \sqrt{0.5} \approx 0.707$$

$$\Rightarrow \hspace{0.3cm} \varphi_2(t) = \left\{ \begin{array}{c} 0.5/0.707 = 0.707\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < 2 \\ 2 \le t < 3 \\ \end{array} \hspace{0.05cm},$$

und schließlich für den zweiten Koeffizienten

$$s_{22} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 1 \cdot 0.707 + 0 \cdot 0.707 \hspace{0.1cm}\hspace{0.15cm}\underline { = 0.707} \hspace{0.05cm}.$$

Die Berechnungen sind in der nachfolgenden Grafik verdeutlicht.

Gram-Schmidt-Berechnungen

(4)  Man erkennt sofort, dass $s_3(t)$ sich als Linearkombination aus $s_1(t)$ und $s_2(t)$ ausdrücken lässt.

$$s_{3}(t) = -s_{1}(t) + s_{2}(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{31} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{11} + s_{21} = -1.414 + 0.707 = \hspace{0.1cm}\hspace{0.15cm}\underline {-0.707}\hspace{0.05cm},$$

$$s_{32} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{12} + s_{22} = 0 + 0.707 \hspace{0.1cm}\underline {= 0.707}\hspace{0.05cm},$$

$$s_{33} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{13} + s_{23} = 0 + 0 \hspace{0.1cm}\underline {= 0}\hspace{0.05cm}.$$

(5)  Der Bereich $2 ≤ t ≤ 3$ wird weder von $\varphi_1(t)$ noch von $\varphi_2(t)$ abgedeckt. Deshalb liefert $s_4(t)$ die neue Basisfunktion $\varphi_3(t)$. Da außerdem $s_4(t)$ nur Anteile im Bereich $2 ≤ t ≤ 3$ aufweist und $||s_4(t)|| = 1$ ist, ergibt sich $\varphi_3(t) = s_4(t)$ sowie

$$s_{41} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{42} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1} \hspace{0.05cm}.$$