Exercise 2.3Z: xDSL Frequency Band

• Return to book

xDSL-Frequenzbandbelegung

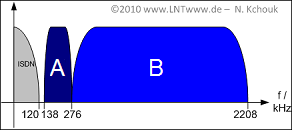
Die Abbildung zeigt die Frequenzbandbelegung eines gebräuchlichen xDSL–Systems:

• Im unteren Bereich befindet sich das ISDN–Band.
• Danach folgen zwei Bänder $\rm A$ und $\rm B$, die für Downstream und Upstream stehen.
• Über die Reihenfolge der beiden Bänder wird nichts ausgesagt. Dies ist die Fragestellung zur Teilaufgabe (2).

Weiter ist bei xDSL/DMT standardisiert, dass

• pro Sekunde $4000$ Rahmen übertragen werden,
• nach $68$ Datenrahmen jeweils ein Synchronisationsrahmen eingefügt wird,
• die Symboldauer wegen des zyklischen Präfix noch um den Faktor $16/17$ verkürzt werden muss,
• jeder Datenrahmen zu einem DMT–Symbol codiert wird.

Damit ist auch die Integrationsdauer $T$ festgelegt, die beim Empfänger zur Detektion ausgewertet wird, und gleichzeitig auch die Grundfrequenz $f_{0} = 1/T$ des hier betrachteten DMT–Verfahrens (Discrete Multitone Transmission) darstellt.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel xDSL als Übertragungstechnik.
• Informationen zum zyklischen Präfix finden Sie im Kapitel Verfahren zur Senkung der Bitfehlerrate bei DSL.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Um welches xDSL–System handelt es sich?

	ADSL,
	ADSL2+,
	VDSL.

2

Wie ist die Reihenfolge von Upstream und Downstream?

	$\rm A$ kennzeichnet den Upstream und $\rm B$ den Downstream.
	$\rm A$ kennzeichnet den Downstream und $\rm B$ den Upstream.

3

Welche Symboldauer $T$ ergibt sich für das DMT-Sytem?

$T \ = \ $ $\ \rm µ s$

4

Welche Grundfrequenz $f_{0}$ liegt dem DMT–Verfahren zugrunde?

$f_{0} \ = \ $ $\ \rm kHz$

5

Wieviele Kanäle $(\hspace{-0.03cm}K_{\rm max}\hspace{-0.03cm})$ könnten in $2208 \ \rm kHz$ übertragen werden?

$K_{\rm max} \ = \ $

6

Wieviele Downstreamkanäle $(\hspace{-0.03cm}K_{\rm down}\hspace{-0.03cm})$ ergeben sich bei diesem System, wenn man die Aussparung der unteren Frequenzen berücksichtigt?

$K_{\rm down} \ = \ $

7

Mit wievielen Bit $(b)$ müssten die Subkanäle im Mittel belegt werden, damit die Bitrate $R_{\rm B} = 25 \ \rm Mbit/s$ beträgt?

$b \ = \ $ $\ \rm bit$

Musterlösung

Solution

(1)  Richtig ist der zweite Lösungsvorschlag:

• Bei ADSL endet das Frequenzband bei $1104 \ \rm kHz$.
• VDSL hat je nach Bandplan eine deutlich größere Bandbreite, wobei sich Upstream– und Downstream–Bänder jeweils abwechseln.

(2)  Richtig ist der erste Lösungsvorschlag:

• Dem Upstream wurden die besseren (niedrigeren) Frequenzen zugewiesen, da sich ein Ausfall der wenigeren Upstream–Kanäle prozentual ungünstiger auswirkt als der Ausfall eines Downstream–Kanals.

(3)  Ohne Berücksichtigung der Synchronisationsrahmen (nach jeweils $68$ nur mit Nutzdaten belegten Rahmen) und des Guard–Intervalls ergäbe sich für die Rahmendauer $T = 1/(4000/{\rm s}) = 250 \ \rm µ s$.

• Mit Berücksichtigung dieses Overheads ist die Symboldauer um den Faktor $68/69 \cdot 16/17$ kürzer:

$$T = \frac{68}{69} \cdot \frac{16}{17} \cdot 250\, {\rm \mu s} \hspace{0.15cm}\underline{ \approx 232\, {\rm µ s}} \hspace{0.05cm}.$$

(4)  Die Subträger liegen bei DMT bei allen Vielfachen von $f_0$, wobei gelten muss:

$$f_0 = \frac{1}{T} \hspace{0.15cm}\underline{= 4.3125 \, {\rm kHz}}.$$

• Die Zeitfensterung entspricht nämlich der Multiplikation der cosinusförmigen Trägersignale mit einer Rechteckfunktion der Dauer $T$.
• Im Frequenzbereich ergibt sich damit die Faltung mit der si–Funktion.
• Würden die Systemgrößen $T$ und $f_0 = 1/T$ nicht aufeinander abgestimmt sein, so käme es zu einer De–Orthogonalisierung der einzelnen DMT–Kanäle und damit zu Intercarrier–Interferenzen.

(5)  Ohne Berücksichtigung der ISDN/Upstream–Reservierung erhält man $K_{\rm max} = 2208/4.3125 \underline{= 512}.$

(6)  Die unteren $276/4.3125 = 64$ Kanäle sind beim hier betrachteten System ADSL2+ für ISDN und Upstream reserviert. Somit verbleiben $K_{\rm down} = 512 – 64\hspace{0.15cm} \underline{= 448}$ nutzbare Kanäle.

(7)  Für die Bitrate gilt

$$R_{\rm B} = 4000 \, \,\frac {\rm Rahmen}{\rm s} \cdot K \cdot b \hspace{0.05cm}.$$

Daraus ergibt sich für die (mittlere) Bitbelegung pro Subkanal (Bin):

$$b = \frac{R_{\rm B}}{ 4000 \, \, {\rm Rahmen}/{\rm s} \cdot K} = \frac{25 \cdot 10^6 \,\, {\rm bit/s}}{ 4000 \, \, {1}/{\rm s} \cdot 448} \hspace{0.15cm}\underline{= 13.95 \, \, {\rm bit}}\hspace{0.05cm}.$$