Decoding of Linear Block Codes

Blockschaltbild und Voraussetzungen

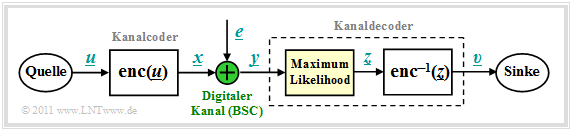
Wir gehen von dem bereits im Kapitel Kanalmodelle und Entscheiderstrukturen gezeigten Blockschaltbild aus, wobei als Kanalmodell meist der Binary Symmetric Channel (BSC) verwendet wird. Zur Codewortschätzung verwenden wir den Maximum–Likelihood–Entscheider (ML), der für binäre Codes ⇒ $\underline{x} \in {\rm GF}(2^n)$ auf Blockebene das gleiche Ergebnis liefert wie der MAP–Empfänger.

Blockschaltbild zur Decodierung von Blockcodes

Die Aufgabe des Kanaldecoders kann wie folgt beschrieben werden:

Der Vektor $\underline{v}$ nach der Decodierung (an der Sinke) soll möglichst gut mit dem Informationswort $\underline{u}$ übereinstimmen. Das heißt: Die Blockfehlerwahrscheinlichkeit soll möglichst klein sein:

\[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]

Aufgrund der deterministischen Zuweisungen $\underline{x} = {\rm enc}(\underline{u})$ bzw. $\underline{v} = {\rm enc}^{-1}(\underline{z})$ gilt aber auch:

\[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]

Gesucht ist somit das zum gegebenen Empfangswort $\underline{y} = \underline{x} +\underline{e}$ am wahrscheinlichsten gesendete Codewort $\underline{x}_i$, das als Ergebnis $\underline{z}$ weiter gegeben wird:

\[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]

Beim BSC–Kanal gilt sowohl $\underline{x}_i \in {\rm GF}(2^n)$ als auch $\underline{y} \in {\rm GF}(2^n)$, so dass die Maximum–Likelihood–Regel auch mit der Hamming–Distanz $d_{\rm H}( \underline{y}, \, \underline{x}_i)$ geschrieben werden kann:

\[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]

Prinzip der Syndromdecodierung

Vorausgesetzt wird hier ein $(n, \, k)$–Blockcode mit der Prüfmatrix $\boldsymbol{\rm H}$ und den systematischen Codeworten

\[\underline{x}\hspace{0.05cm} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) = (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k})\hspace{0.05cm}. \]

Mit dem Fehlervektor $\underline{e}$ gilt dann für das Empfangswort:

\[\underline{y} = \underline{x} + \underline{e} \hspace{0.05cm}, \hspace{0.4cm} \underline{y} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{x} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.4cm} \underline{e} \in \hspace{0.1cm} {\rm GF}(2^n) \hspace{0.05cm}.\]

Ein Bitfehler an der Position $i$, das heißt $y_i ≠ x_i$, wird ausgedrückt durch den Fehlerkoeffizienten $e_i = 1$.

$\text{Definition:}$ Das Syndrom $\underline{s} = (s_0, s_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, s_{m-1})$ berechnet sich (als Zeilen– bzw. Spaltenvektor) aus dem Empfangswort $\underline{y}$ und der Prüfmatrix $\boldsymbol{\rm H}$ in folgender Weise:

\[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T}\hspace{0.3cm}{\rm bzw.}\hspace{0.3cm} \underline{s}^{\rm T} = { \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T}\hspace{0.05cm}.\]

Die Vektorlänge von $\underline{s}$ ist gleich $m = n-k$ (Zeilenzahl von $\boldsymbol{\rm H}$).

Das Syndrom $\underline{s}$ zeigt folgende Charakteristika:

Wegen der Gleichung $\underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{0}$ hängt das Syndrom $\underline{s}$ nicht vom Codewort $\underline{x}$ ab, sondern allein vom Fehlervektor $\underline{e}$:

\[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{x} \cdot { \boldsymbol{\rm H}}^{\rm T} + \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \hspace{0.05cm} \underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} \hspace{0.05cm}.\]

Bei hinreichend wenig Bitfehlern liefert $\underline{s}$ einen eindeutigen Hinweis auf die Fehlerpositionen und ermöglicht so eine vollständige Fehlerkorrektur.

$\text{Beispiel 1:}$ Ausgehend vom systematischen $\text{(7, 4, 3)}$–Hamming–Code erhält man für den Empfangsvektor $\underline{y} = (0, 1, 1, 1, 0, 0, 1)$ das folgende Ergebnis:

\[{ \boldsymbol{\rm H} } \cdot \underline{y}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \underline{s}^{\rm T} \hspace{0.05cm}.\]

Vergleicht man das Syndrom mit den Prüfgleichungen des Hamming–Codes, so erkennt man, dass

am wahrscheinlichsten das vierte Symbol $(x_4 = u_4)$ des Codewortes verfälscht wurde,

der Codewortschätzer somit das Ergebnis $\underline{z} = (0, 1, 1, 0, 0, 0, 1)$ liefern wird.

die Entscheidung nur dann richtig ist, wenn bei der Übertragung nur ein Bit verfälscht wurde.

Nachfolgend sind die erforderlichen Korrekturen für den $\text{(7, 4, 3)}$–Hamming–Code angegeben, die sich aus dem errechneten Syndrom $\underline{s}$ entsprechend den Spalten der Prüfmatrix ergeben:

\[\underline{s} = (0, 0, 0) \hspace{0.10cm} \Rightarrow\hspace{0.10cm}{\rm keine\hspace{0.15cm} Korrektur}\hspace{0.05cm};\hspace{0.8cm}\underline{s} = (1, 0, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm}p_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\]

\[\underline{s} =(0, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{1.22cm}\underline{s} = (1, 0, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_1{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\]

\[\underline{s} =(0, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} p_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{1.22cm}\underline{s} = (1, 1, 0)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_3{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\]

\[\underline{s} =(0, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_4{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm};\hspace{1.22cm}\underline{s} = (1, 1, 1)\hspace{0.10cm} \Rightarrow\hspace{0.10cm} u_2{\rm \hspace{0.15cm} invertieren}\hspace{0.05cm}. \]

Verallgemeinerung der Syndromdecodierung

Wir gehen weiterhin vom BSC–Kanalmodell aus. Das bedeutet:

Der Empfangsvektor $\underline{y}$ und der Fehlervektor $\underline{e}$ sind Elemente von ${\rm GF}(2^n)$.
Die möglichen Codeworte $\underline{x}_i$ gehören zum Code $\mathcal{C}$, der einen $(n-k)$–dimensionalen Untervektorraum von ${\rm GF}(2^n)$ aufspannt.

Unter dieser Voraussetzung fassen wir die Ergebnisse der letzten Seiten nochmals kurz zusammen:

Die Syndromdecodierung ist eine Realisierungsmöglichkeit der Maximum–Likelihood–Detektion von Blockcodes. Man entscheidet sich für das Codewort $\underline{x}_i$ mit der geringsten Hamming–Distanz zum Empfangswort $\underline{y}$ :

\[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]

Die Syndromdecodierung ist aber auch die Suche nach dem wahrscheinlichsten Fehlervektor $\underline{e}$, der die Bedingung $\underline{e} \cdot { \boldsymbol{\rm H}}^{\rm T} = \underline{s}$ erfüllt. Das Syndrom liegt dabei durch $\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} $ fest.

Mit dem Hamming–Gewicht $w_{\rm H}(\underline{e})$ kann die zweite Interpretation auch wie folgt mathematisch formuliert werden:

\[\underline{z} = \underline{y} + {\rm arg} \min_{\underline{e}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} {\rm GF}(2^n)} \hspace{0.1cm} w_{\rm H}(\underline{e}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]

$\text{Fazit:}$ Zu beachten ist, dass der Fehlervektor $\underline{e}$ ebenso wie der Empfangsvektor $\underline{y}$ ein Element von ${\rm GF}(2^n)$ ist im Gegensatz zum Syndrom $\underline{s} \in {\rm GF}(2^m)$ mit der Anzahl $m = n-k$ der Prüfgleichungen. Das bedeutet,

dass die Zuordnung zwischen Syndrom $\underline{s}$ und Fehlervektor $\underline{e}$ nicht eindeutig ist, sondern

dass jeweils $2^k$ Fehlervektoren zum gleichen Syndrom $\underline{s}$ führen, die man zu einer Nebenklasse (englisch: Coset ) zusammenfasst.

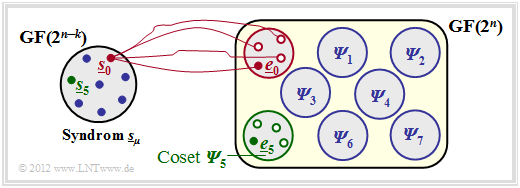
$\text{Beispiel 2:}$ Der Sachverhalt soll hier am Beispiel $n = 5, k = 2$ ⇒ $m = n-k = 3$ verdeutlicht werden.

Aufteilung $2^k$ der Fehlervektoren in Cosets

Man erkennt aus dieser Grafik:

Die $2^n = 32$ möglichen Fehlervektoren $\underline{e}$ werden in $2^m = 8$ „Cosets” ${\it \Psi}_0$, ... , ${\it \Psi}_7$ aufgeteilt.
Explizit gezeichnet sind hier nur die Cosets ${\it \Psi}_0$ und ${\it \Psi}_5$.

Alle $2^k = 4$ Fehlervektoren des Cosets ${\it \Psi}_\mu$ führen zum gleichen Syndrom $\underline{s}_\mu$.
Jede Nebenklasse ${\it \Psi}_\mu$ hat einen Anführer $\underline{e}_\mu$, nämlich denjenigen mit dem minimalen Hamming–Gewicht.

$\text{Beispiel 3:}$ Ausgehend vom systematischen $\text{(5, 2, 3)}$–Code $\mathcal{C} = \big \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \big \}$ wird nun die Vorgehensweise bei der Syndromdecodierung im Detail beschrieben.

Beispielhafte $\text{(5, 2, 3)}$–Syndromtabelle mit Nebenklassen

Generatormatrix und Prüfmatrix lauten:

\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 &0 &1 &1 &0 \\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},\]

\[{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &0 &1 &0 &0 \\ 1 &1 &0 &1 &0 \\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.\]

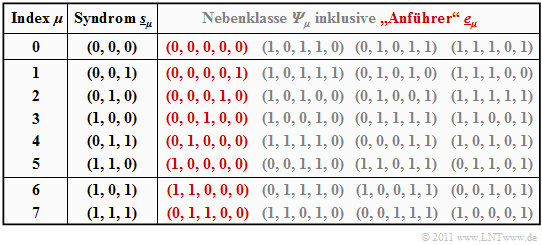
Die Tabelle fasst das Endergebnis zusammen. Beachten Sie:

Der Index $\mu$ ist nicht identisch mit dem Binärwert von $\underline{s}_\mu$.
Die Reihenfolge ergibt sich vielmehr durch die Anzahl der Einsen im Nebenklassenanführer $\underline{e}_\mu$.
Beispielsweise ist das Syndrom $\underline{s}_5 = (1, 1, 0)$ und das Syndrom $\underline{s}_6 = (1, 0, 1)$.

Zur Herleitung dieser Tabelle ist anzumerken:

Die Zeile 1 bezieht sich auf das Syndrom $\underline{s}_0 = (0, 0, 0)$ und die dazugehörige Nebenklasse ${\it \Psi}_0$. Am wahrscheinlichsten ist hier die Fehlerfolge $(0, 0, 0, 0, 0)$ ⇒ kein Bitfehler, die wir als Nebenklassenanführer $\underline{e}_0$ bezeichnen.
Auch die weiteren Einträge in der ersten Zeile, nämlich $(1, 0, 1, 1, 0 )$, $(0, 1, 0, 1, 1)$ und $(1, 1, 1, 0, 1 )$, liefern jeweils das Syndrom $\underline{s}_0 = (0, 0, 0)$, ergeben sich aber nur mit mindestens drei Bitfehlern und sind entsprechend unwahrscheinlich.

In den Zeilen 2 bis 6 beinhaltet der jeweilige Nebenklassenanführer $\underline{e}_\mu$ genau eine einzige Eins ($\mu = 1$, ... , $5$). $\underline{e}_\mu$ ist stets das wahrscheinlichste Fehlermuster der Klasse ${\it \Psi}_\mu$. Die anderen Gruppenmitglieder ergeben sich erst bei mindestens zwei Bitfehlern.

Das Syndrom $\underline{s}_6 = (1, 0, 1)$ ist mit nur einem Bitfehler nicht möglich. Bei der Erstellung der Tabelle wurden daraufhin alle $5\text{ über }2 = 10$ Fehlermuster $\underline{e}$ mit Gewicht $w_{\rm H}(\underline{e}) = 2$ betrachtet.
Die zuerst gefundene Folge mit Syndrom $\underline{s}_6 = (1, 0, 1)$ wurde als Nebenklassenanführer $\underline{e}_6 = (1, 1, 0, 0, 0)$ ausgewählt. Bei anderer Probierreihenfolge hätte sich auch die Folge $(0, 0, 1, 0, 1)$ aus ${\it \Psi}_6$ ergeben können.

Ähnlich wurde bei der Bestimmung des Anführers $\underline{e}_7 = (0, 1, 1, 0, 0)$ der Nebenklasse ${\it \Psi}_7$ vorgegangen, die durch das einheitliche Syndrom $\underline{s}_7 = (1, 1, 1)$ gekennzeichnet ist. Auch in der Klasse ${\it \Psi}_7$ gibt es eine weitere Folge mit Hamming–Gewicht $w_{\rm H}(\underline{e}) = 2$, nämlich $(1, 0, 0, 0, 1)$.

Die obige Tabelle muss nur einmal erstellt und kann beliebig oft genutzt werden. Zunächst muss das Syndrom ermittelt werden. Dieses lautet beispielsweise für den Empfangsvektor $\underline{y} = (0, 1, 0, 0, 1)$:

\[\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H} }^{\rm T} = \begin{pmatrix} 0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 &1 &0 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \\ \end{pmatrix} = \begin{pmatrix} 0 &1 &0 \end{pmatrix}= \underline{s}_2 \hspace{0.05cm}.\]

Mit dem Nebenklassenanführer $\underline{e}_2 = (0, 0, 0, 1, 0)$ aus obiger Tabelle (roter Eintrag für Index 2) gelangt man schließlich zum Decodierergebnis:

\[\underline{z} = \underline{y} + \underline{e}_2 = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1) + (0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0) = (0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1) \hspace{0.05cm}.\]

$\text{Fazit:}$ Aus dieser Kurzzusammenfassung geht schon hervor, dass die Syndromdecodierung mit einem enormen Aufwand verbunden ist, wenn man nicht wie bei zyklischen Codes gewisse Eigenschaften nutzen kann:

Bei großen Blockcodelängen versagt diese Methode vollständig. So müsste man zur Decodierung eines BCH–Codes – die Abkürzung steht für deren Erfinder Bose, Chaudhuri und Hocquenghem – mit den Codeparametern $n = 511$, $k = 259$ und $d_{\rm min} = 61$ genau $2^{511-259} \approx 10^{76}$ Fehlermuster der Länge $511$ auswerten und abspeichern.
Für diese Codes und auch für andere Codes großer Blocklänge gibt es aber spezielle Decodieralgorithmen, die mit weniger Aufwand zum Erfolg führen.

Codiergewinn – Bitfehlerrate bei AWGN

Wir betrachten nun die Bitfehlerrate (englisch: Bit Error Rate , BER) für folgende Konstellation:

Bitfehlerrate bei $\text{(7, 4, 3)}$–Hamming–Codierung

Hamming–Code $\text{HC (7, 4, 3)}$,

AWGN–Kanal, gekennzeichnet durch den Quotienten $E_{\rm B}/N_0$ (in dB),

Maximum–Likelihood–Detektion (ML) mit Hard Decision bzw. Soft Decision.

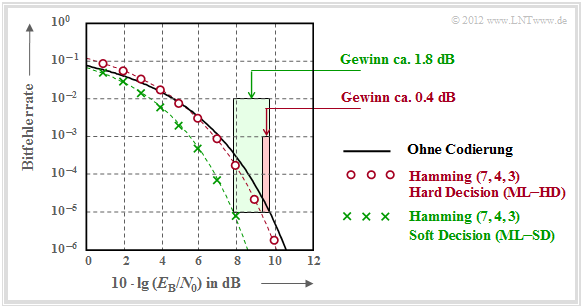
Zu dieser Grafik ist anzumerken:

Die schwarze Vergleichskurve gilt beispielsweise für die binäre Phasenmodulation (BPSK) ohne Codierung. Hierfür benötigt man für die Bitfehlerrate $10^{-5}$ etwa $10 \cdot \lg \, E_{\rm B}/N_0 = 9.6 \, \rm dB$.

Die roten Kreise gelten für den $\text{(7, 4, 3)}$–Code und harte Entscheidungen des Maximum–Likelihood–Decoders $\text{(ML–HD)}$. Die Syndromdecodierung ist hierfür eine mögliche Realisierungsform.

Diese Systemkonfiguration bringt erst für $10 \cdot \lg \, E_{\rm B}/N_0 >6 \, \rm dB$ eine Verbesserung gegenüber dem Vergleichssystem. Für $\rm BER =10^{-5}$ benötigt man nur noch $10 \cdot \lg \, E_{\rm B}/N_0 \approx 9.2 \, \rm dB$.

Die grünen Kreuze für den Hamming–Code mit Soft–Decision $\text{(ML–SD)}$ liegen im gesamten Bereich unterhalb der Vergleichskurve. Für $\rm BER =10^{-5}$ ergibt sich $10 \cdot \lg \, E_{\rm B}/N_0 \approx 7.8 \, \rm dB$.

$\text{Definition:}$ Als Codiergewinn einer Systemkonfiguration (gekennzeichnet durch seinen Code und die Art der Decodierung) bezeichnen wir das gegenüber dem Vergleichssystem (ohne Codierung) kleinere $10 \cdot \lg \, E_{\rm B}/N_0$, das für eine vorgegebene Bitfehlerrate $\rm (BER)$ erforderlich ist:

\[G_{\rm Code} (\hspace{0.05cm}{\rm System}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) =10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 \hspace{0.15cm}(\hspace{0.05cm}{\rm ohne\hspace{0.1cm} Codierung}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm})- 10 \cdot {\rm lg}\hspace{0.1cm}{E}_{\rm B}/N_0 \hspace{0.15cm}(\hspace{0.05cm}{\rm System}\hspace{0.05cm}\vert\hspace{0.05cm}{\rm BER}\hspace{0.05cm}) \hspace{0.05cm}. \]

Angewendet auf obige Grafik erhält man:

\[G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-HD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 0.4\ {\rm dB}\hspace{0.05cm},\]

\[G_{\rm Code} (\hspace{0.05cm}{\rm Hamming \hspace{0.1cm}(7,\hspace{0.02cm}4,\hspace{0.02cm}3), ML-SD}\hspace{0.05cm}|\hspace{0.05cm}{\rm BER} = 10^{-5}\hspace{0.05cm}) = 1.8\ {\rm dB}\hspace{0.05cm}.\]

Decodierung beim Binary Erasure Channel

Abschließend soll noch gezeigt werden, in wie weit der Decoder zu modifizieren ist, wenn anstelle des BSC–Modells (Binary Symmetrie Channel) das BEC–Kanalmodell (Binary Erasure Channel) zum Einsatz kommt, der keine Fehler produziert, sondern unsichere Bit als Auslöschungen markiert.

$\text{Beispiel 4:}$ Ohne Einschränkung der Allgemeingültigkeit betrachten wir wie im Beispiel 3 wieder den systematischen (5, 2, 3)–Blockcode $\mathcal{C} = \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm}(0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \}$

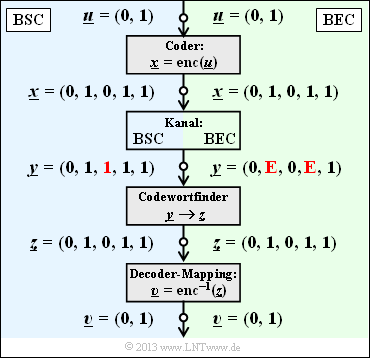
Zur Fehlerkorrektur bei BSC und BEC

Nebenstehende Grafik zeigt das Systemmodell und gibt beispielhafte Werte für die einzelnen Vektoren wider.

Der linke Bildteil (blau hinterlegt) gilt für das BSC–Modell mit einem Bitfehler $0 → 1$ beim dritten Bit.
Der rechte Bildteil (grün hinterlegt) gilt für das BEC–Modell und zeigt zwei Erasures $\rm 1 → E$ bei Bit 2 und 4.

Man erkennt:

Bei BSC kann wegen $d_{\rm min} = 3$nur ein Bitfehler korrigiert werden ($t = 1$, rot markiert). Beschränkt man sich auf Fehlererkennung, so funktioniert diese bis zu $e= d_{\rm min} -1 = 2$ Bitfehler.

Bei BEC macht Fehlererkennung keinen Sinn, denn bereits der Kanal lokalisiert ein unsicheres Bit als Erasure E (Auslöschung). Die Nullen und Einsen im BEC–Empfangswort $\underline{y}$ sind sicher. Deshalb funktioniert hier die Fehlerkorrektur bis zu $e = 2$ Auslöschungen mit Sicherheit.

Auch $e = 3$ Auslöschungen sind manchmal noch korrigierbar. So kann $\underline{y} \rm = (E, E, E, 1, 1)$ zu $\underline{z} \rm = (0, 1, 0, 1, 1)$ korrigiert werden, da kein zweites Codewort mit zwei Einsen endet. Dagegen ist $\underline{y} \rm = (0, E, 0, E, E)$ aufgrund des im Code erlaubten Nullwortes nicht korrigierbar.

Wird sichergestellt, dass in keinem Empfangswort mehr als zwei Auslöschungen vorkommen, so ist die BEC–Blockfehlerwahrscheinlichkeit ${\rm Pr}(\underline{z} \ne \underline{x}) = {\rm Pr}(\underline{v} \ne \underline{u}) \equiv 0$. Dagegen hat die entsprechende Blockfehlerwahrscheinlichkeit beim BSC–Modell stets einen Wert größer als $0$.

Da nach dem BEC ein jedes Empfangswort entweder richtig oder gar nicht decodiert wird, nennen wir hier den Block $\underline{y} → \underline{z}$ zukünftig „Codewortfinder”. Eine „Schätzung” findet nur beim BSC–Modell statt.

Wie funktioniert aber nun die Decodierung eines Empfangswortes $\underline{y}$ mit Auslöschungen algorithmisch?

$\text{Beispiel 5:}$ Ausgehend vom Empfangswort $\underline{y} \rm = (0, E, 0, E, 1)$ im Beispiel 4 setzen wir den Ausgang des Codewortfinders formal zu $\underline{z} \rm = (0, z_2, 0, z_4, 1)$, wobei die Symbole $z_2 \in \{0, \, 1\}$ und $z_4 \in \{0, \, 1\}$ entsprechend folgender Gleichung zu bestimmen sind:

\[\underline{z} \cdot { \boldsymbol{\rm H} }^{\rm T}= \underline{0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}.\]

Es geht nun darum, diese Bestimmungsgleichung möglichst effizient umzusetzen. Es ergeben sich folgende Rechenschritte:

Mit der Prüfmatrix $\boldsymbol{\rm H}$ des (5, 2, 3)–Blockcodes und dem Vektor $\underline{z} \rm = (0, z_2, 0, z_4, 1)$ lautet die obige Bestimmungsgleichung:

\[{ \boldsymbol{\rm H} } \cdot \underline{z}^{\rm T} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ z_2 \\ 0 \\ z_4 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \hspace{0.05cm}.\]

Wir fassen die sicheren (korrekten) Bit zum Vektor $\underline{z}_{\rm K}$ zusammen und die ausgelöschten Bit zum Vektor $\underline{z}_{\rm E}$. Dann teilen wir die Prüfmatrix $\boldsymbol{\rm H}$ in die entsprechenden Teilmatrizen $\boldsymbol{\rm H}_{\rm K}$ und $\boldsymbol{\rm H}_{\rm E}$ auf:

\[\underline{z}_{\rm K} =(0, 0, 1)\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm K}= \begin{pmatrix} 1 &1 &0\\ 1 &0 &0\\ 0 &0 &1 \end{pmatrix} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {\rm Spalten\hspace{0.15cm} 1,\hspace{0.15cm}3 \hspace{0.15cm}und \hspace{0.15cm}5 \hspace{0.15cm}der \hspace{0.15cm}Pr\ddot{u}fmatrix} \hspace{0.05cm},\]

\[\underline{z}_{\rm E} = (z_2, z_4)\hspace{0.05cm},\hspace{0.35cm} { \boldsymbol{\rm H} }_{\rm E}= \begin{pmatrix} 0 &0\\ 1 &1\\ 1 &0 \end{pmatrix} \hspace{0.9cm}\Rightarrow\hspace{0.3cm} {\rm Spalten\hspace{0.15cm} 2 \hspace{0.15cm}und \hspace{0.15cm}4 \hspace{0.15cm}der \hspace{0.15cm}Pr\ddot{u}fmatrix} \hspace{0.05cm}.\]

Unter Berücksichtigung der Tatsache, dass in $\rm GF(2)$ die Subtraktion gleich der Addition ist, lässt sich die obige Gleichung wie folgt darstellen:

\[{ \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} + { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= \underline{0}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} }_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H} }_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} 0 &0\\ 1 &1\\ 1 &0 \end{pmatrix} \cdot \begin{pmatrix} z_2 \\ z_4 \end{pmatrix} = \begin{pmatrix} 1 &1 &0\\ 1 &0 &0\\ 0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \hspace{0.05cm}.\]

Dies führt zu einem linearen Gleichungssystem mit zwei Gleichungen für die unbekannten $z_2$ und $z_4$ (jeweils $0$ oder $1$). Aus der letzten Zeile folgt $z_2 = 1$ und aus der zweiten Zeile $z_2 + z_4 = 0$ ⇒ $z_4 = 1$. Damit ergibt sich das zulässige Codewort $\underline{z} \rm = (0, 1, 0, 1, 1)$.