Error Probability and Application Areas

1. Channel Coding
2. Reed–Solomon–Codes und deren Decodierung
3. Error Probability and Application Areas

• Previous page
• Next page

• Previous page
• Next page

Blockfehlerwahrscheinlichkeit für RSC und BDD

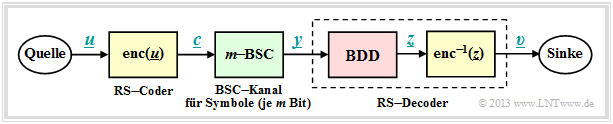
Zur Fehlerwahrscheinlichkeitsberechnung gehen wir vom gleichen Blockschaltbild wie im Kapitel Fehlerkorrektur nach Reed–Solomon–Codierung aus, wobei wir uns hier für den Codewortschätzer $(\underline {y} → \underline {z})$ auf Bounded Distance Decoding (BDD) beschränken. Für Maximum Likelihood Decoding  sind die Ergebnisse geringfügig besser.

Systemmodell mit Reed–Solomon–Codierung, $m$–BSC und Bounded Distance Decoding

Die Blockfehlerwahrscheinlichkeit sei wie folgt definiert:

$${ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{v} \ne \underline{u})= { \rm Pr}( \underline{z} \ne \underline{c}) = { \rm Pr}( f >t) \hspace{0.05cm}.$$

Aufgrund der BDD–Annahme ergibt sich das gleiche einfache Ergebnis wie für die binären Blockcodes, nämlich die Wahrscheinlichkeit dafür, dass die Anzahl $f$  der Fehler im Block (Empfangswort) größer ist als die Korrekturfähigkeit $t$ des Codes. Da für die Zufallsgröße $f$ (Fehleranzahl) eine Binominalverteilung im Bereich $0 ≤ f ≤ n$ vorliegt, erhält man:

$${\rm Pr(Blockfehler)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$

Während aber im ersten Hauptkapitel stets $c_i ∈ \rm GF(2)$ gegolten hat und damit die $f$ Übertragungsfehler jeweils Bitfehler waren, versteht man bei Reed–Solomon–Codierung unter einem Übertragungsfehler $(y_i \ne c_i)$ wegen $c_i ∈ {\rm GF}(2^m)$ sowie $y_i ∈ {\rm GF}(2^m)$ einen Symbolfehler. Damit ergeben sich folgende Unterschiede:

• Das diskrete Kanalmodell zur Beschreibung der binären Blockcodes ist der Binary Symmetric Channel (BSC). Jedes Bit $c_i$ eines Codewortes wird mit der Wahrscheinlichkeit $\varepsilon$ verfälscht $(y_i \ne c_i)$ und mit der Wahrscheinlichkeit $1-\varepsilon$ richtig übertragen $(y_i = c_i)$.
  

• Bei Reed–Solomon–Codierung muss man das BSC–Modell durch das $m$–BSC–Kanalmodell ersetzen. Ein Symbol $c_i$ wird mit der Wahrscheinlichkeit $\varepsilon_{\rm S}$ in ein anderes Symbol $y_i$ verfälscht (egal, in welches) und kommt mit der Wahrscheinlichkeit $1-\varepsilon_{\rm S}$ unverfälscht beim Empfänger an.
  
  

$\text{Beispiel 1:}$  Wir gehen vom BSC–Parameter $\varepsilon = 0.1$ aus und betrachten Reed–Solomon–Codesymbole $c_i ∈ {\rm GF}(2^8)$   ⇒   $m = 8$, $q = 256$, $n = 255$.

Für eine Symbolverfälschung $(y_i \ne c_i)$ genügt bereits ein falsches Bit. Oder anders ausgedrückt: Soll $y_i = c_i$ gelten, so müssen alle $m = 8$ Bit des Codesymbols richtig übertragen werden:

$$1 - \varepsilon_{\rm S} = (1 - \varepsilon)^m = 0.9^8 \approx 0.43 \hspace{0.05cm}.$$

• Damit ergibt sich für das 8–BSC–Modell die Verfälschungswahrscheinlichkeit $\varepsilon_{\rm S} ≈ 0.57$.
• Mit der weiteren Annahme, dass die Verfälschung von $c_i = \beta$ in jedes andere Symbol $y_i = \gamma \ne \beta$ gleichwahrscheinlich ist, erhält man:

$${\rm Pr}(y_i = \gamma\hspace{0.05cm}\vert \hspace{0.05cm}c_i = \beta = 0.57/255 ≈ 0.223\%.$$

Anwendung der Reed–Solomon–Codierung bei binären Kanälen

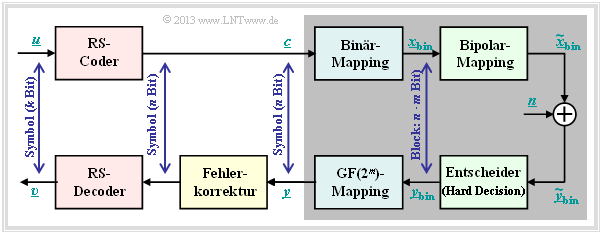
Die Voraussetzungen für die folgende Berechnung der Blockfehlerwahrscheinlichkeit eines Systems mit Reed–Solomon–Codierung und Umsetzung auf Binärsymbole sind in der Grafik zusammengefasst:

• Angenommen wird eine $(n, k)$–Reed–Solomon–Codierung mit Symbolen aus $c_i ∈ {\rm GF}(2^m)$. Je kleiner die Coderate $R=k/m$ ist, um so weniger Information kann bei fester Datenrate übertragen werden.
  

• Jedes Symbol wird durch $m$ Bit binär dargestellt   ⇒   Binär–Mapping. Ein Block (Codewort $\underline {c}$) besteht somit aus $n$ Symbolen bzw. aus $n \cdot m$ Binärzeichen (Bit), die in $\underline {c}_{\rm bin}$ zusammengefasst werden.
  

• Vorausgesetzt wird außerdem der AWGN–Kanal, gekennzeichnet durch den Parameter $E_{\rm B}/N_0$. Entsprechend diesem Kanalmodell geschieht die Übertragung bipolar:   „0”   ↔   $+1$ sowie „1”   ↔ $-1$.

• Der Empfänger trifft harte Entscheidungen (Hard Decision) auf Bitebene. Vor der Decodierung inclusive der Fehlerkorrektur werden die Binärsymbole wieder auf ${\rm GF}(2^m)$–Symbole umgesetzt.
  

Anwendung der Reed–Solomon–Codierung bei Binärkanälen

Die auf der letzten Seite angegebene Gleichung (gültig für Bounded Distance Decoding),

$${\rm Pr(Blockfehler)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm},$$

basiert auf dem $m$–BSC–Kanal. Ausgehend vom AWGN–Kanal kommt man

• mit dem komplementären Gaußschen Fehlerintegral ${\rm Q}(x)$ zum BSC–Parameter

$$\varepsilon = {\rm Q} \big (\sqrt{2 \cdot E_{\rm S}/N_0} \big ) = {\rm Q} \big (\sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \big ) \hspace{0.05cm},$$

• und daraus zur Verfälschungswahrscheinlichkeit $\varepsilon_{\rm S}$ auf Symbolebene:

$$\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m \hspace{0.05cm}.$$

$\text{Beispiel 2:}$  Für $R=k/n = 239/255 = 0.9373$, $10 \cdot \lg \ E_{\rm B}/N_0 = 7 \, \rm dB$   ⇒   $E_{\rm B}/N_0 ≈ 5$ und $n = 2^8-1$ 1   ⇒   $m = 8$ erhält man für den Parameter $\varepsilon_{\rm S}$ des 8–BSC–Modells:

$$\varepsilon = {\rm Q} \big (\sqrt{2 \cdot 0.9373 \cdot 5} \big ) = {\rm Q} \big (3.06\big ) \approx 1.1 \cdot 10^{-3} \hspace{0.05cm}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \varepsilon_{\rm S} = 1 - (1 - 1.1 \cdot 10^{-3})^8 = 1 - 0.9989^8 = 1 - 0.9912 \approx 0.88 \cdot \% \hspace{0.05cm}.$$

Jedes einzelne Symbol wird also mit mehr als $99$–prozentiger Wahrscheinlichkeit fehlerfrei übertragen.

BER der Reed–Solomon–Codierung bei binären Kanälen

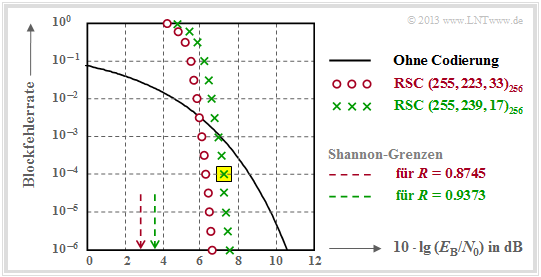
Die folgende Grafik zeigt die in [Liv10] angegebenen Blockfehlerwahrscheinlichkeiten in Abhängigkeit des AWGN–Quotienten $10 \cdot \lg \ E_{\rm B}/N_0$.

Blockfehlerwahrscheinlichkeit zweier Reed–Solomon–Codes der Länge $n = 255$

Dargestellt sind die berechneten Kurvenverläufe ${ \rm Pr}( \underline{v} \ne \underline{u})$ für zwei verschiedene Reed–Solomon–Codes entsprechend den Deep Space Standards nach CCSDS (Consultative Committee for Space Data Systems), nämlich

• dem $\text{RSC (255, 239, 17)}_{256}$ mit $R=0.9373$, der bis zu $t = 8$ Fehler korrigieren kann, und
  
• dem $\text{RSC (255, 223, 33)}_{256}$ mit höherer Korrekturfähigkeit $(t = 16)$ aufgrund kleinerer Coderate.

Hinweis:   Die nachfolgend nur angedeutete Berechnung sollen Sie in der Aufgabe 2.15 für den $\text{RSC (7, 3, 5)}_{8}$ – also für etwas übersichtlichere Parameter – vollständig durchführen.
Wir analysieren den in der Grafik gelb hinterlegten Punkt, gültig für den $\text{RSC (255, 239, 17)}_{256}$, und $10 \cdot \lg \ E_{\rm B}/N_0 = 7.1 \,\rm dB$   ⇒   $\varepsilon = 0.007$. Die dazugehörige Blockfehlerwahrscheinlichkeit ergibt sich entsprechend der Grafik zu

$${\rm Pr(Blockfehler)} = \sum_{f =9}^{255} {255 \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{255-f}\approx 10^{-4} \hspace{0.05cm}.$$

Dominant ist hierbei der erste Term (für $f=9$), der bereits etwa $80\%$ ausmacht:

$${255 \choose 9} \approx 1.1 \cdot 10^{16}\hspace{0.05cm},\hspace{0.15cm} \varepsilon_{\rm S}^9 \approx 4 \cdot 10^{-20}\hspace{0.05cm},\hspace{0.15cm} (1 -\varepsilon_{\rm S})^{246} \approx 0.18 \hspace{0.15cm} \Rightarrow \hspace{0.15cm} {\rm Pr}(f = 9) \approx 8 \cdot 10^{-5} \hspace{0.05cm}.$$

Dies soll als Beleg dafür gelten, dass man die Summation schon nach wenigen Termen abbrechen darf.

Die in der Grafik dargestellten Ergebnisse kann man wie folgt zusammenfassen:

• Für kleines $E_{\rm B}/N_0$ (des AWGN–Kanals) sind die Reed–Solomon–Codes völlig ungeeignet. Beide Codes liegen für $10 \cdot \lg \ E_{\rm B}/N_0 < 6 \,\rm dB$ über der (schwarzen) Vergleichskurve für uncodierte Übertragung.
  

• Die Berechung für den $\text{RSC (255, 223, 33)}_{256}$ unterscheidet sich von obiger Rechnung nur in der unteren Summationsgrenze $(f_{\rm min} = 17)$ und durch ein etwas größeres $\varepsilon_{\rm S}$ (wegen $R = 0.8745$).
  

• Dieser $(t = 16)$–Code ist für $\rm BER = 10^{-6}$ auch nur um etwa $1 \, \rm dB$ besser als der durch grüne Kreuze gekennzeichnete Code mit $t = 8$. Die Ergebnisse beider Codes sind also eher enttäuschend.
  

$\text{Fazit:}$ 

• Reed–Solomon–Codes sind beim gedächtnislosen Binärkanal (AWGN–Kanal) nicht sehr gut. Beide Codes liegen mehr als $4 \, \rm dB$ von der informationstheoretischen Shannon–Grenze entfernt.
  

• Reed–Solomon–Codes sind dagegen sehr wirkungsvoll bei so genannten Bündelfehlerkanälen. Sie werden deshalb vorwiegend bei Fadingkanälen, Speichersysteme, usw. eingesetzt.
  
• Die Reed–Solomon–Codes sind nicht perfekt. Welche Konsequenzen sich daraus ergeben, wird in der Aufgabe 2.16 behandelt.

Typische Anwendungen mit Reed–Solomon–Codierung

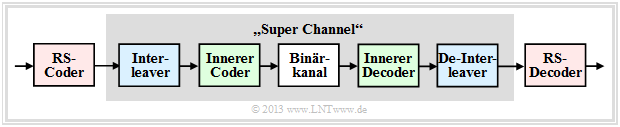
Reed–Solomon–Codierung wird häufig entsprechend der Grafik zusammen mit einem inneren Code  in kaskadierter Form angewandt.

• Der innere Code ist fast immer ein Binärcode und in der Satelliten– und Mobilkommunikation oft ein Faltungscode.
• Will man nur die Reed–Solomon–Codierung/Decodierung untersuchen, so ersetzt man in einer Simulation die grau hinterlegten Komponenten durch einen einzigen Block, den man „Super Channel” nennt.
  

Codeschema mit Kaskadierung

Besonders effizient ist ein solches verkettetes (englisch: concatenated) Codiersystem, wenn zwischen den beiden Codierern ein Interleaver geschaltet ist, um Bündelfehler weiter zu entspreizen.

$\text{Beispiel 3:}$  Die Grafik zeigt beispielhaft einen solchen Interleaver, wobei wir uns auf eine $20 × 4$– Matrix beschränken. In der Praxis sind diese Matrizen deutlich größer.

Interleaver–Matrix für $20 × 4$ Symbole

Der Interleaver wird zeilenweise beschrieben und spaltenweise ausgelesen (blaue Beschriftung). Beim De–Interleaver (grüne Beschriftung) ist die Reihenfolge genau umgekehrt.

• Die Reed–Solomon–Symbole werden also nicht fortlaufend an den inneren Coder weitergeleitet, sondern entsprechend der angegebenen Reihenfolge als Symbol 1, 21, 41, 61, 2, 22, usw. .
  

• Auf dem Kanal wird ein zusammenhängender Bereich (hier die Symbole 42, 62, 3, 23, 43, 63, 4, 24   ⇒   um das rot umrandete Rechteck) zerstört, zum Beispiel durch einen Kratzer auf dem Kanal „Speichermedium”.
  

• Nach dem De–Interleaving ist die Symbolreihenfolge wieder 1, 2, 3, ...     Man erkennt an den rot umrandeten Kreisen, dass nun dieses Fehlerbündel weitgehend „aufgebrochen” wurde.

$\text{Beispiel 4:}$  Eine sehr weit verbreitete Anwendung von Reed–Solomon–Codierung – und zudem die kommerziell erfolgreichste – ist die Compact Disc  $\rm (CD)$, deren Fehlerkorrekturmechanismus bereits im Einführungkapitel dieses Buches beschrieben wurde. Hier ist der innere Code ebenfalls ein Reed–Solomon–Code, und das verkette Codiersystem lässt sich wie folgt beschreiben:

• Beide Kanäle des Stereo–Audiosignals werden mit je $\text{44.1 kHz}$ abgetastet und jeder einzelne Abtastwert wird mit $32$ Bit (vier Byte) digital dargestellt.
  

• Die Gruppierung von sechs Samples ergibt einen Rahmen ($192$ Bit) und damit $24$ Codesymbole aus dem Galoisfeld $\rm GF(2^8)$. Jedes Codesymbol entspricht somit genau einem Byte.
  

• Der erste Reed–Solomon–Code mit der Rate $R_1 = 24/28$ liefert $28$ Byte, die einem Interleaver der Größe $28 × 109$ Byte zugeführt werden. Das Auslesen erfolgt (kompliziert) diagonal.
  

• Der Interleaver verteilt zusammenhängende Bytes großräumig über die gesamte Disk. Dadurch werden so genannte Bursts „aufgelöst”, die zum Beispiel durch Kratzer auf der $\rm CD$ herrühren.
  

• Zusammen mit dem zweiten Reed–Solomon–Code (Rate $R_2 = 28/32$) ergibt sich eine Gesamtrate von $R = (24/28) · (28/32) = 3/4$. Beide Codes können jeweils $t = 2$ Symbolfehler korrigieren.
  

• Die beiden Komponentencodes $\text{RSC (28, 24, 5)}$ und $\text{RSC (32, 28, 5)}$ basieren jeweils auf dem Galoisfeld $\rm GF(2^8)$, was eigentlich die Codelänge $n = 255$ bedeuten würde.
  

• Die hier benötigten kürzeren Komponentencodes ergeben sich aus aus dem $\text{RSC (255, 251, 5)}_{256}$ durch Shortening   ⇒   siehe Aufgabe 1.9Z. Durch diese Maßnahme wird die minimale Distanz $d_{\rm min}= 5$ nicht verändert.
  

• Mit der anschließenden Eight–to–Fourteen–Modulation und weiterer Kontrollsymbole kommt man schließlich zur endgültigen Coderate $R = 192/588 ≈ 0.326$ der CD–Datenkomprimierung.
  
  

Auf der Seite Geschlitzte CD kann man sich anhand eines Audio–Beispiels von der Korrekturfähigkeit dieser cross–interleaved Reed–Solomon–Codierung überzeugen, aber auch deren Grenzen erkennen.

Aufgaben zum Kapitel

Aufgabe 2.15: RS-Blockfehlerwahrscheinlichkeit bei AWGN

Aufgabe 2.15Z: Nochmals RS-Blockfehlerwahrscheinlichkeit

Aufgabe 2.16: BDD–Entscheidungskriterien