Exercise 3.9Z: Convolution of Gaussian Pulses

• Return to book

Gaußförmige $x(t)$ und $h(t)$

Es soll das Faltungsergebnis zweier Gaußfunktionen ermittelt werden. Wir betrachten einen gaußförmigen Eingangsimpuls ${x(t)}$ mit der Amplitude $x_0 = 1\,\text{ V}$ und der äquivalenten Dauer $\Delta t_x = 4 \,\text{ms}$ sowie eine ebenfalls gaußförmige Impulsantwort ${h(t)}$, welche die äquivalente Dauer $\Delta t_h = 3 \,\text{ms}$ aufweist:

$$x( t ) = x_0 \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_x } )^2 } ,$$

$$h( t ) = \frac{1}{\Delta t_h } \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_h } )^2 } .$$

Gesucht ist das Ausgangssignal ${y(t)} = {x(t)} ∗{h(t)}$, wobei der Umweg über die Spektralfunktionen gegangen werden soll.

Hinweise:

• Die Aufgabe gehört zum Kapitel Faltungssatz und Faltungsoperation.

Fragebogen

1

Geben Sie die Spektralfunktionen ${X(f)}$ und ${H(f)}$ an. Welche Werte ergeben sich für $f = 0$?

$X(f = 0)\ = \ $  $\text{mV/Hz}$

$H(f = 0)\ = \ $

2

Berechnen Sie die Spektralfunktion ${Y(f)}$ des Ausgangssignals. Wie groß ist der Spektralwert bei $f = 0$?

$Y(f = 0)\ = \ $  $\text{mV/Hz}$

3

Berechnen Sie den Ausgangsimpuls ${y(t)}$. Welche Werte ergeben sich für die Amplitude $y_0 = y(t = 0)$ und die äquivalente Impulsdauer $\Delta t_y$?

$y_0\ = \ $  $\text{V}$

$\Delta t_y\ = \ $  $\text{ms}$

Musterlösung

Solution

(1)  Durch Fouriertransformation erhält man:

$$X( f ) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x \cdot f} \right)^2 } , \hspace{0.5cm}H(f) = {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_h \cdot f} \right)^2 } .$$

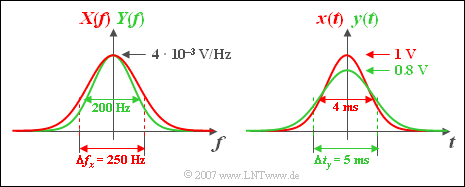
Die gesuchten Werte sind $X(f = 0)\;\underline{ = 4 \,\text{mV/Hz}}$ und $H(f = 0)\; \underline{= 1}$.

Faltungsergebnis für „$\rm Gauß \ \ast \ Gauß$”

(2)  Der Faltung im Zeitbereich entspricht die Multiplikation im Frequenzbereich:

$$Y(f) = X(f) \cdot H(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x^2 + \Delta t_h^2 } \right)f^2 } .$$

Mit der Abkürzung $\Delta t_y = (\Delta t_x^2 + \Delta t_h^2)^{1/2} = 5\, \text{ms}$ kann hierfür auch geschrieben werden:

$$Y(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \cdot f} \right)^2 } .$$

• Bei der Frequenz $f = 0$ sind die Spektralwerte am Eingang und Ausgang des Gaußfilters gleich, also gilt:

$$Y(f = 0) \;\underline{= 4 \text{mV/Hz}}.$$

• Der Funktionsverlauf von ${Y(f)}$ ist schmaler als ${X(f)}$ und auch schmaler als ${H(f)}$.

(3)  Es gilt die folgende Fourierkorrespondenz:

$${\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \cdot f} \right)^2 }\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{1}{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$

Damit erhält man:

$$y(t) = x(t) * h(t) = x_0 \cdot \frac{\Delta t_x }{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$

• Der Maximalwert des Signals ${y(t)}$ liegt ebenfalls bei $t = 0$ und beträgt $y_0 \hspace{0.15cm}\underline{= 0.8 V}$.
• Die äquivalente Impulsdauer ergibt sich zu $\Delta t_y \hspace{0.15cm}\underline{= 5 \text{ms}}$ (siehe obiges Bild, rechte Skizze).
• Das bedeutet: Das Gaußfilter ${H(f)}$ bewirkt, dass der Ausgangsimpuls ${y(t)}$ kleiner und breiter als der Eingangsimpuls ${x(t)}$ ist.
• Die Impulsform bleibt weiterhin gaußförmig.