Exercise 1.17Z: BPSK Channel Capacity
Gemäß dem Kanalcodierungstheorem lassen sich Binärsignale über den AWGN–Kanal dann und nur dann fehlerfrei übertragen, wenn
- man einen Kanalcode der Rate $R = k/n$ verwendet,
- die Blocklänge $n$ dieses Codes sehr groß gewählt wird ⇒ $n → ∞$,
- die Rate $R$ kleiner ist als die für binären Eingang gültige Kanalkapazität $C_{2}$,
- wobei die BPSK–Kanalkapazität $C_{2}$ vom AWGN–Quotienten $E_{\rm B}/N_{0}$ abhängt.
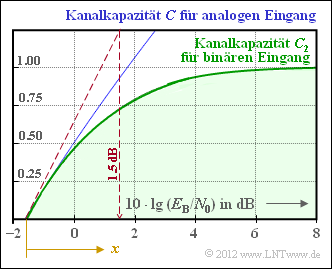
Der zulässige Bereich für die Coderate $R$ ist in der Grafik grün hinterlegt. Die Grenzkurve $C_{2}$, gültig für binäre Eingangssignale $($daher der Index $2)$ und manchmal auch als BPSK–Kanalkapazität bezeichnet (steht für Binary Phase Shift Keying), ist allerdings nicht in mathematisch–geschlossener Form angebbar, sondern das Ergebnis eines Integrals, das nur numerisch ausgewertet werden kann.
Als blaue Kurve ist die Kanalkapazität $C$ eingetragen, wenn man beliebige reelle Eingangssignale zulässt.
- Bei mehrstufigen Signalen kann die Rate durchaus auch Werte $R > 1$ annehmen.
- Für eine Gaußverteilung ergibt sich für die Rate $R$ das kleinstmögliche $(E_{\rm B}/N_{0})_{\rm min}$ gemäß der Gleichung
- $$\left (E_{\rm B}/N_0 \right)_{\rm min} = \frac{2^{2R}-1}{2R}\hspace{0.05cm}.$$
Im Umkehrschluss ist die Rate $R$ für den gegebenen AWGN–Quotienten $E_{\rm B}/N_{0}$ nach oben begrenzt:
- Die gerade noch zulässige Coderate $R_{\rm max}$ bei gegebenem Kanal $(E_{\rm B}/N_{0} = \rm const.)$ bezeichnen wir als die Kanalkapazität $C$.
- Für $E_{\rm B}/N_{0} = 1 ⇒ 10 · \ \lg {E_{\rm B}/N_0} = 0 {\rm dB}$ erhält man beispielsweise $C = 0.5$.
- Das heißt: Auch bei bestmöglicher Amplitudenverteilung des reellen Eingangssignals darf die Coderate den Wert $R = 0.5$ nicht überschreiten.
- Bei binärem Eingang ergibt sich ein etwas kleinerer Wert gemäß $C_{2}.$
In dieser Aufgabe soll versucht werden, den grafisch vorgegebenen Verlauf der Kanalkapazität $C_{2}$ durch eine Exponentialfunktion anzunähern:
- Verwenden Sie für die Abszisse die Hilfsvariable (siehe Grafik)
- $$x = \frac {x_0 + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}\hspace{0.05cm}.$$
- Das heißt: $x$ ist ohne Einheit; auf die Pseudo–Einheit „$\rm dB$” wird verzichtet.
- Berücksichtigen Sie, dass für ein kleines $E_{\rm B}/N_{0}$ die Näherung $C_{2} \approx C$ gültig ist (siehe Grafik), woraus der Parameter $x_{0}$ bestimmt werden kann.
- Setzen Sie für $C_{2}\hspace{0.01cm}' = 1 - {\rm e}^{–a\hspace{0.05cm} · \hspace{0.05cm}x}$ an und bestimmen Sie den Parameter $a$ aus der gestrichelt eingezeichneten Tangente derart, dass $C_{2}\hspace{0.01cm} ' \approx C$ gilt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Informationstheoretische Grenzen der Kanalcodierung. Sie ergänzt die Aufgabe 1.17.
- Auf die Pseudo–Einheit „bit/Kanalzugriff” der Kanalkapazität wird in diesen Aufgaben verzichtet.
Fragebogen
Musterlösung
(1) Im unteren $E_{\rm B} /N_{0}$–Bereich laufen die Kapazitätskurven
- $C_{2}$ (gültig für binären Eingang, zum Beispiel BPSK) und
- $C$ (gültig für analogen reellwertigen Eingang)
zusammen. Für eine gegebene Rate $R$ muss $E_{\rm B}/N_{0}$ größer sein als $(2^{2R} – 1)/2R.$
Der Grenzübergang für $R → 0$ liefert die absolute Shannon–Grenze, ab der eine fehlerfreie Übertragung nicht mehr möglich ist:
- $${\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] = \lim_{R \rightarrow 0}\hspace{0.1cm} \frac{2^{2R}-1}{2R} = {\rm ln}\hspace{0.1cm}2 \approx 0.693\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} {\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] \approx -1.6 \,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_0 \hspace{0.15cm} \underline{= 1.6 \,{\rm dB}}\hspace{0.05cm}.$$
(2) Aus der Grafik auf der Angabenseite lässt sich die Tangentensteigerung im Nullpunkt abschätzen:
- $$\frac{{\rm d}C_2}{{\rm d}x} (x=0) = \frac{1.6 + 1.5}{1.25} =2.48 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} a = \frac{1}{2.48} \hspace{0.15cm} \underline{\approx 0.4}\hspace{0.05cm}.$$
Damit lautet die Näherung für die BPSK–Kanalkapazität in Abhängigkeit des Abszissenwertes $x$:
- $$C_2' = \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}x} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r\hspace{0.15cm}} x > 0, \\{\rm f\ddot{u}r\hspace{0.15cm}} x < 0. \end{array}$$
(3) Aus $E_{\rm B} = N_{0}$ folgt $\ 10 · \lg {(E_{\rm B} = N_0)} = 0 \ {\rm dB}$ sowie $x = 1.6$:
- $$C_2' = 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}1.6}\hspace{0.15cm}\underline{\approx 0.47}\hspace{0.05cm}.$$
(4) Die entsprechenden Zahlenwerte lauten:
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{2 dB:} \hspace{0.3cm} C_2' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}3.6}\hspace{0.15cm}\underline{\approx 0.76}$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}5.6}\hspace{0.15cm}\underline{\approx 0.89}$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}7.6}\hspace{0.15cm}\underline{\approx 0.95}.$$
Die so angenäherten Werte $C_{2}'$ der Kanalkapazität für binären Eingang sind etwas zu klein.
Aus der Grafik auf der Angabenseite können die genauen Werte $C_{2}$ abgeschätzt werden:
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 =\text{2 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.78}\hspace{0.05cm},$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.94}\hspace{0.05cm},$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.99}\hspace{0.05cm}.$$
Ab etwa $\ 10 · \lg {(E_{\rm B} / N_0)} = 8 \ {\rm dB}$ gilt innerhalb der Zeichengenauigkeit $C_{2}'= C_{2} = 1$ (bit/Kanalzugriff).