Exercise 5.1Z: Sampling of Harmonic Oscillations
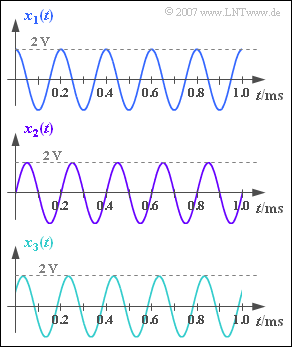
Wir betrachten drei harmonische Schwingungen mit gleicher Frequenz und gleicher Amplitude:
- $$x_1(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_2(t) = A \cdot \sin (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_3(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - 60^{\circ}) \hspace{0.05cm}.$$
Die Schwingungsparameter $f_0$ und $A$ können Sie der Grafik entnehnen.
Angenommen wird, dass die Signale äquidistant zu den Zeitpunkten $\nu \cdot T_{\rm A}$ abgetastet werden, wobei die Parameterwerte $T_{\rm A} = 80 \ µ \text{s}$ und $T_{\rm A} = 100 \ µ \text{s}$ analysiert werden sollen.
Die Signalrekonstruktion beim Empfänger erfolgt durch einen Tiefpass $H(f)$, der aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ das Signal $y(t)$ formt. Es gelte:
- $$H(f) = \left\{ \begin{array}{c} 1 \\ 0.5 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_{\rm G} \hspace{0.05cm}, \\ |f| = f_{\rm G} \hspace{0.05cm}, \\ |f| > f_{\rm G} \hspace{0.05cm}, \\ \end{array}$$
Hierbei gibt $f_{\rm G}$ die Grenzfrequenz des rechteckförmigen Tiefpassfilters an. Für diese soll gelten:
- $$f_{\rm G} = \frac{1}{ 2 \cdot T_{\rm A}}\hspace{0.05cm}.$$
Das Abtasttheorem ist erfüllt, wenn $y(t) = x(t)$ gilt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zeitdiskrete Signaldarstellung.
- Zu der hier behandelten Thematik gibt es ein interaktives Applet: Abtastung periodischer Signale & Signalrekonstruktion
Fragebogen
Musterlösung
(2) Richtig sind alle Löungsvorschläge:
- Die Abtastrate ist hier $f_{\rm A} = 1/T_{\rm A} = 12.5 \ \text{kHz}$.
- Dieser Wert ist größer als $2 \cdot f_0 = 10 \ \text{kHz}$.
- Damit ist das Abtasttheorem unabhängig von der Phase erfüllt, und es gilt stets $y(t) = x(t)$.
(3) Die Abtastrate beträgt nun $f_{\rm A} = 2 \cdot f_0 = 10 \ \text{kHz}$.
- Nur im Sonderfall des Cosinussignals ist nun das Abtasttheorem erfüllt und es gilt:
- $$y_1(t) = x_1(t)$ ⇒ $A_1 \; \underline{=2 \ \text{V}} \text{ und }\varphi_1 \; \underline{= 0}.$$
Dieses Ergebnis soll nun noch mathematisch hergeleitet werden, wobei im Hinblick auf die noch anstehenden Teilaufgaben bereits auch eine Phase $\varphi$ im Eingangssignal berücksichtigt wird:
- $$x(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - \varphi) \hspace{0.05cm}.$$
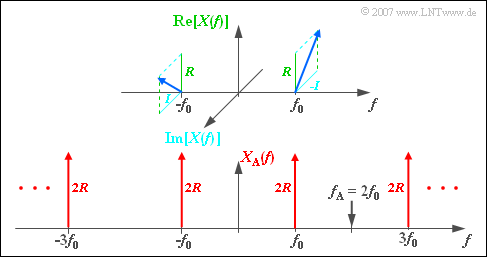
Dann gilt für die Spektralfunktion, die in der oberen Grafik skizziert ist:
- $$X(f) = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f+ f_{\rm 0} ) + {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
Mit den Abkürzungen
- $$R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi) \hspace{0.5cm}{\rm und} \hspace{0.5cm}I ={A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin(\varphi)$$
kann hierfür auch geschrieben werden:
- $$X(f) = (R + {\rm j} \cdot I) \cdot \delta (f+ f_{\rm 0} ) + (R - {\rm j} \cdot I) \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
Das Spektrum des mit $f_{\rm A} = 2f_0$ abgetasteten Signals $x_{\rm A}(t)$ lautet somit:
- $$X_{\rm A}(f) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )= \sum_{\mu = - \infty }^{+\infty} X (f- 2\mu \cdot f_{\rm 0} )\hspace{0.05cm}.$$
- Die untere Grafik zeigt, dass $X_{\rm A}(f)$ aus Diracfunktionen bei $\pm f_0$, $\pm 3f_0$, $\pm 5f_0$, usw. besteht.
- Alle Gewichte sind rein reell und gleich $2 \cdot R$.
- Die Imaginärteile des periodisch fortgesetzten Spektrums heben sich auf.
Berücksichtigt man weiter den rechteckförmigen Tiefpass, dessen Grenzfrequenz exakt bei $f_{\rm G} = f_0$ liegt, sowie $H(f_{\rm G}) = 0.5$, so erhält man für das Spektrum nach der Signalrekonstruktion:
- $$Y(f) = R \cdot \delta (f+ f_{\rm 0} ) + R \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}, \hspace{0.5cm} R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi)\hspace{0.05cm}.$$
Die Fourierrücktransformation führt auf
- $$y(t) = A \cdot \cos (\varphi)\cdot \cos (2 \pi \cdot f_0 \cdot t ) \hspace{0.05cm}.$$
- Es ergibt sich also unabhängig von der Eingangsphase $\varphi$ ein cosinusförmiger Verlauf.
- Ist $\varphi = 0$ wie beim Signal $x_1(t)$, so ist auch die Amplitude des Ausgangssignals gleich $A$.
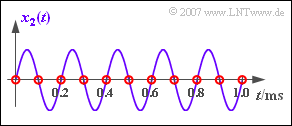
(4) Das Sinussignal hat die Phase $90^\circ$. Daraus folgt direkt $y_2(t) = 0$ ⇒ Amplitude $\underline{A_2 = 0}$.
- Dieses Ergebnis wird verständlich, wenn man sich die Abtastwerte in der Grafik betrachtet.
- Alle Abtastwerte (rote Kreise) sind $0$, so dass auch nach dem Filter kein Signal vorhanden sein kann.
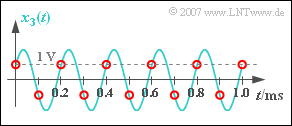
(5) Trotz $\varphi = 60^\circ$ gilt $\varphi_3 = 0$ ⇒ auch das rekonstruierte Signal $y_3(t)$ ist cosinusförmig. Die Amplitude ist gleich
- $$A_3 = A \cdot \cos (60^{\circ})= {A}/{2} \hspace{0.15 cm}\underline{= 1\,{\rm V}} \hspace{0.05cm}.$$
- Wenn Sie die rot eingezeichneten Abtastwerte in der Grafik betrachten, so werden Sie zugeben, dass Sie als „Signalrekonstrukteur” keine andere Entscheidung treffen würden als der Tiefpass.
- Sie kennen ja den türkisfarbenen Verlauf nicht.