Exercise 1.6Z: Comparison of Rayleigh and Rice

Phasendiagramm des Faktors $z(t) = x(t) + {\rm j} \cdot y(t)$
bei Rayleigh und Rice

In dieser Aufgabe sollen Rayleigh–Fading und Rice–Fading miteinander verglichen werden.

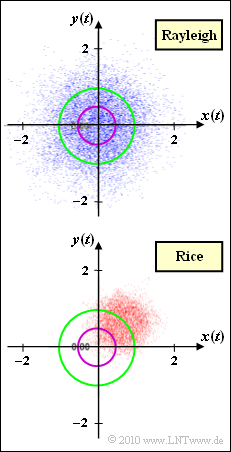
Die Grafik zeigt den komplexen Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ in der komplexen Ebene. Für das Tiefpass–Sendesignal $s(t) = 1$, was bezüglich eines Bandpass–Systems einer Cosinusschwingung mit der Amplitude $1$ entspricht, ist das Tiefpass–Empfangssignal $r(t)$ identisch mit $z(t)$.

Das obere Diagramm beschreibt Rayleigh–Fading, wobei die Komponentensignale $x(t)$ und $y(t)$ jeweils gaußverteilt sind mit der Varianz $\sigma^2$. Die Wahrscheinlichkeitsdichtefunktion des Betrags $a(t) = |z(t)|$ lautet für $a ≥ 0$:

$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 }{2\sigma^2}] \hspace{0.05cm}.$$

Der quadratische Erwartungswert von $z(t)$ ist $1$:

$${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma = {1}/{\sqrt{2}} \approx 0.707 \hspace{0.05cm}.$$

Das untere Phasendiagramm entsteht bei Rice–Fading. Auch hier sind $x(t)$ und $y(t)$ gaußverteilt mit der Varianz $\sigma^2$, aber nun mit Mittelwert $x_0$ bzw. $y_0$. Die WDF lautet mit der modifizierten Besselfunktion ${\rm I}_0$ für $a ≥ 0$:

$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} \left[ -\frac{a^2 + |z_0|^2}{2\sigma^2}\right] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}.$$

Der quadratische Mittelwert beinhaltet nun auch die Direktkomponente $z_0 = x_0 + {\rm j} \cdot y_0$:

$${\rm E}\left [ |z(t)|^2 \right ] = 2 \cdot \sigma^2 + |z_0|^2 \hspace{0.05cm}.$$

Für den Systemvergleich

ist von konstantem ${\rm E}\big[|z(t)|^2\big] = 1$ auszugehen,
wird beim Rice–Fading von der aus der Grafik erkennbaren Vorzugsrichtung ausgegangen,
sei die Leistung zwischen dem Direktpfad $(|z_0|^2)$ und den Streupfaden $(2\sigma^2)$ im Verhältnis $4:1$ aufgeteilt.

Für die Teilaufgaben (1) bis (4) gelte $s(t) = 1$, während in den Teilaufgaben (5) bzw. (6) ein BPSK–Signal vorausgesetzt wird. Das Tiefpass–Signal $s(t)$ hat somit einen rechteckförmigen Verlauf mit den möglichen Werten $±1$. Die Dauer eines Rechteckimpulses sei $T = 10 \ \rm ms$.

Hinweise:

Die Aufgabe gehört zum Kapitel Nichtfrequenzselektives Fading mit Direktkomponente.
Die in der Grafik eingezeichneten Kreise (violett und grün) beziehen sich auf die Teilaufgaben (3) und (4).

Fragebogen

Musterlösung

Solution

(1) Richtig ist der Lösungsvorschlag 2:

Der erste Vorschlag liefert ein Rayleigh–Fading–Modell. Mit der letzten Einstellung ergäbe sich:

$$|z(t)| = {\rm j} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = s(t) \cdot z(t) = {\rm j} \cdot s(t) \hspace{0.05cm}.$$

Berücksichtigen wir, dass wir uns im äquivalenten Tiefpassbereich befinden, so würde dann bei einem cosinusförmigen Eingang ein minus–sinusförmiges Ausgangssignal $r_{\rm BP}(t)$ auftreten.
Dagegen gilt mit dem Lösungsvorschlag 2 für alle möglichen Signale:

$$|z(t)| = x_0 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = s(t) \hspace{0.05cm}.$$

(2) Beim gegebenem Rayleigh–Fading beträgt der Parameter $\sigma^2 = 0.5$. Damit ergibt sich für den quadratischen Mittelwert des multiplikativen Faktors $z(t)$:

$${\rm E}\left [ |z(t)|^2 \right ] = 2 \sigma^2 = 1 \hspace{0.05cm}.$$

Das Rice–Fading soll genau die gleiche Leistung besitzen. Das heißt, es soll gelten:

$$|z_0|^2 + 2 \sigma^2 = 1 \hspace{0.05cm}.$$

Weiterhin wurde gefordert:

Das Verhältnis der Leistungen von deterministischen Anteil ($|z_0|^2$) und stochastischem Anteil ($2\sigma^2$) sei $4$. Daraus folgt:

$$2 \sigma^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma^2 = 0.1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \frac{1}{\sqrt{10}} \hspace{0.25cm} \underline{ \approx 0.316} \hspace{0.05cm},$$

$$|z_0|^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |z_0| = 0.894 \hspace{0.05cm}.$$

Die Aufteilung von $z_0 = x_0 + {\rm j} \cdot y_0$ ergibt sich aus der Grafik. Man erkennt, dass $y_0 = x_0$ sein muss (Mittelpunkt der Wolke im ersten Quadranten unter $45^\circ$):

$$x_0 = y_0 = \frac{|z_0|}{\sqrt{2}} = \frac{0.894}{\sqrt{2}} \hspace{0.25cm} \underline{ \approx 0.632} \hspace{0.05cm}.$$

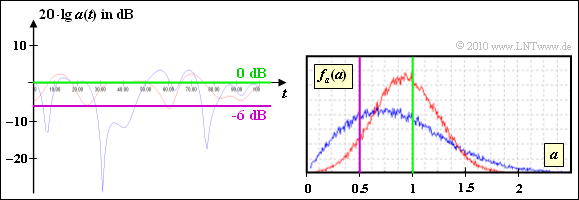
(3) Der Bereich „$20 \cdot {\rm lg} \, |z(t)| ≤ \, –6 \ \rm dB$” ist gleich bedeutend mit „$|z(t)|≤0.5$”.

Dieser Bereich ist in der Grafik auf der Angabenseite durch den violetten Kreis markiert.
Man erkennt daraus, dass die Aussage 1 richtig ist, da sich bei Rayleigh mehr Punkte innerhalb des violetten Kreises befinden.

Signalausschnitt und WDF $f_a(a)$ bei Rayleigh und Rice

Diese Grafik zeigt das Ergebnis einer Systemsimulation mit dem Programm „Mobilfunkkanal” aus dem (früheren) Praktikum „Simulation digitaler Übertragungssysteme”.

Sowohl aus dem Signalausschnitt als auch aus der WDF erkennt man, dass die blaue Kurve (Rayleigh) mehr Anteile unter der violetten Kurve besitzt als die rote Kurve (Rice).

(4) Richtig ist Lösungsvorschlag 3:

Für die Rayleighverteilung ergibt sich die Wahrscheinlichkeit

$${\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a(t) \le 0\,\,{\rm dB}) = {\rm Pr}(a(t) \le 1) = 1 - {\rm e}^{-1} \approx 63\,\,\% \hspace{0.05cm}.$$

Aus der Grafik erahnt man, dass sich für die Riceverteilung (mit den gewählten Parametern) etwa die gleiche Unterschreitungswahrscheinlichkeit ergibt.
Auch aus der komplexen Darstellung von $z(t)$ auf der Angabenseite ist dieses Ergebnis zu erahnen (leichter dann, wenn man das Ergebnis schon kennt).
Unter anderem deshalb, weil die Spitze der Gaußwolke noch innerhalb des grünen Kreises liegt.

Komplexes Empfangssignal $r(t)$ bei Rayleigh und Rice

(5) Richtig sind die Lösungsvorschläge 2 und 3:

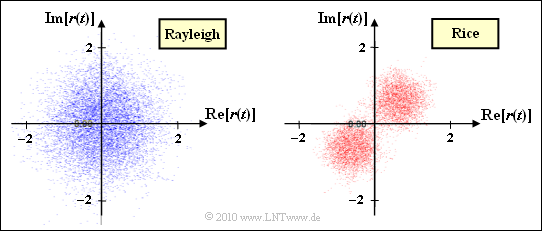
Bei Rice–Fading liegt die Punktwolke von $z(t)$ im ersten Quadranten. Multipliziert man $z(t)$ mit $s(t) = ±1$, so erhält man zwei Punktwolken im ersten und dritten Quadranten. An der WDF $f_a(a)$ des Betrags ändert sich dadurch nichts.
Auch beim Rayleigh–Fading weisen die Dichtefunktionen $f_a(a)$ des Betrags für $|z(t)|$ und $|r(t)|$ keine Unterschiede auf. Da zudem die Phase $\phi$ gleichverteilt ist, ergeben sich im Endergebnis auch gleiche Punktwolken.
Betrachtet man allerdings die Entstehung der komplexen Darstellung von $z(t)$ und $r(t)$ dynamisch, so gibt es sehr wohl Unterschiede.
Bei der komplexen Darstellung von $r(t)$ treten größere Sprünge auf, immer dann, wenn es im Sendesignal $s(t)$ zu Phasensprüngen um $±180^\circ$ kommt, also bei Symbolwechseln.
Somit unterscheiden sich bei Rice–Fading auch ${\it \Phi}_z(f_{\rm D})$ und ${\it \Phi}_r(f_{\rm D})$ – letzteres ist breiter – und dementsprechend auch die zugehörigen Autokorrelationsfunktion.

	Rayleigh–Fading bewirkt Punktwolken in Quadrant $1$ und $3$.
	Rice–Fading bewirkt Punktwolken in Quadrant $1$ und $3$.
	Bei Rayleigh ist die WDF von $\|r(t)\|$ gleich der WDF von $\|z(t)\|$.
	Bei Rice ist die WDF von $\|r(t)\|$ gleich der WDF von $\|z(t)\|$.

	Mit $x_0 = y_0 = 0, \ \ \sigma^2 = 1$.
	Mit $x_0 = 1, \ \ y_0 = 0, \ \ \sigma^2 = 0$.
	Mit $x_0 = 0, \ \ y_0 = 1, \ \ \sigma^2 = 0$.

	Beim vorliegenden Rayleigh–Kanal.
	Beim vorliegenden Rice–Kanal.
	Die Wahrscheinlichkeiten sind näherungsweise gleich.