Exercise 2.2: Simple Two-Path Channel Model

• Return to book

Zwei äquivalente Modelle
für den Zweiwege-Kanal

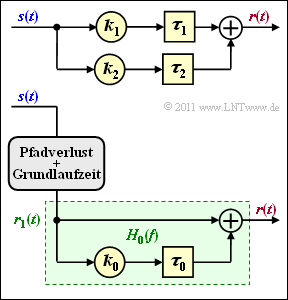
Wir betrachten hier einen Zweiwege–Kanal für den Mobilfunk entsprechend nebenstehender Grafik, gekennzeichnet durch die Modellparameter

$$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \tau_{1} = 10\,{\rm µ s}\hspace{0.05cm}, \hspace{0.2cm}\tau_{2} = 11\,{\rm µ s} \hspace{0.05cm}.$$

Für den Dämpfungsfaktor auf dem Nebenpfad werden zwei verschiedene Zahlenwerte betrachtet:

• $k_2 = 2 \cdot 10^{-5}$   ⇒   Teilaufgaben (1) bis (4),
• $k_2 = 10^{-4}$   ⇒   Teilaufgaben (5) und (6).

Unten ist ein äquivalentes Kanalmodell dargestellt, wobei nur der grün hinterlegte Teil weiter betrachtet wird. Das heißt:  

• Die Grunddämpfung (Pfadverlust) und die Grundlaufzeit werden hierbei außer Betracht gelassen.
• Der Frequenzgang dieses  $(k_0, \tau_0$)–Modells wird mit  $H_0(f)$  bezeichnet.

Eine wichtige Beschreibungsgröße eines jeden Mobilfunksystems ist die Kohärenzbandbreite  $B_{\rm K}$, die im Kapitel  GWSSUS–Kanalmodell  definiert wird. Anhand dieser lässt sich entscheiden, ob das System als nichtfrequenzselektiv eingeschätzt werden kann:

• Dies ist gerechtfertigt, wenn die Signalbandbreite  $B_{\rm S}$  deutlich kleiner ist als die Kohärenzbandbreite  $B_{\rm K}$.
• Andernfalls ist das Mobilfunksystem frequenzselektiv, was eine kompliziertere Beschreibung erfordert.

Als eine einfache Näherung für die Kohärenzbandbreite verwendet man in der Literatur häufig den Kehrwert der Impulsverbreiterung (in unserem Lerntutorial durch ein Hochkomma gekennzeichnet):

$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels  Mehrwegeempfang beim Mobilfunk.
• Für die Lösung benötigen Sie auch die Lichtgeschwindigkeit  $c = 3 \cdot 10^8 \ \rm m/s$.
• Für  $k_2$  werden hier nur positive Werte verwendet. Sie erinnern sich vielleicht:   Entsteht der Nebenpfad durch Reflexion an einer Wand, so ist eigentlich eine Phasenänderung um  $\pi$  zu berücksichtigen, woraus ein negativer  $k_2$–Wert resultiert.

Fragebogen

1

Welche Länge  $d_1$  weist der direkte Pfad auf?

$d_1 \ = \ $ $\ \rm km$

2

Wie lauten die Parameter des vereinfachten Modells für  $k_2 = 2 \cdot 10^{-5}$?

$k_0 \ = \ $

$\tau_0 \ = \ $ $\ \rm µ s$

3

Berechnen Sie den Betragsfrequenzgang   ⇒   $|H_0(f)|$  des vereinfachten Modells für die Frequenzen  $f = 0$,  $f = 250 \ \rm kHz$  und  $f = 500 \ \rm kHz$.

$|H_0(f = 0)| \ = \ $

$|H_0(f = 250 \ \rm kHz)| \ = \ $

$|H_0(f = 500 \ \rm kHz)| \ = \ $

4

Welche Signalfrequenzen  $f_{\rm S}$  bewirken hier destruktive Überlagerungen?

	$f_{\rm S} = 500 \ \rm kHz$,
	$f_{\rm S} = 750 \ \rm kHz$,
	$f_{\rm S} = 1 \ \rm MHz$.

5

Welche Kohärenzbandbreite ergibt sich für  $k_2 = 2 \cdot 10^{-5}$  bzw.  $k_2 = 10^{-4}$  nach der einfachen Näherung?

$k_2 = 2 \cdot 10^{-5} \text{:} \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' = \ $ $\ \rm MHz$

$k_2 = 10^{-4} \text{:} \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' = \ $ $\ \rm MHz$

6

Welche Aussagen sind bezüglich der Frequenzselektivität richtig, wenn  $B_{\rm S}$  die Signalbandbreite bezeichnet?

	Für GSM:   $(B_{\rm S} = 200 \ \rm kHz)$  ist der Kanal frequenzselektiv.
	Für UMTS:   $(B_{\rm S} = 5 \ \rm MHz)$  ist der Kanal frequenzselektiv.

Musterlösung

Solution

(1)  Es gilt $\tau_1 = d_1/c$  ⇒  $d_1 = \tau_1 \cdot c = 10^{-5} \rm s \cdot 3 \cdot 10^8 \ m/s \ \underline {= 3 \ km}$.

(2)  Der Dämpfungsfaktor ist $k_0 = k_2/k_1 \ \underline {= 0.2}$ und die Verzögerungszeit $\tau_0 = \tau_2 \ – \tau_1 \ \underline {= 1 \ \rm µ s}$.

• Der für beide Pfade wirksame Pfadverlust ist damit $k_1 = 10^{-4}$ und die Grundlaufzeit beträgt $\tau_1 = 10 \ \rm µ s$.

(3)  Die Impulsantort lautet:

$$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$

Durch Fouriertransformation kommt man zum Frequenzgang

$$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_0}=1 + k_0 \cdot {\cos}( 2 \pi f \tau_0) + {\rm j}\cdot k_0 \cdot {\sin }( 2 \pi f \tau_0) \hspace{0.05cm},$$

und damit zu folgendem Betragsfrequenzgang:

$$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$

$$|H_{\rm 0}(f = 250\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi/2)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi/2)} = \sqrt{1+ k_0^2} \hspace{0.1cm} \underline {\approx 1.02} \hspace{0.05cm},$$

$$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$

Betragsfrequenzgang eines Zweiwegekanals

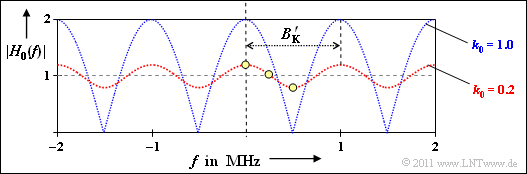
Die Grafik (rote Kurve) zeigt den Funktionsverlauf $|H_0(f)|$.

• Die gesuchten Werte sind durch die gelben Punkte markiert.
• Die blaue Kurve bezieht sich auf die Teilaufgabe (5) mit $k_0 = 1 \ \Rightarrow \ k_2 = k_0 \cdot k_1 = 10^{–4}$.

(4)  Richtig ist der Lösungsvorschlag 1:

• Destruktive Überlagerungen gibt es für $|H_0(f)| < 1$, zum Beispiel für $f = 500 \ \rm kHz$.
• Dagegen gilt:

$$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$

$$|H_{\rm 0}(f = 1\,{\rm MHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 0)| = 1.2 > 1 \hspace{0.05cm}.$$

(5)  Die Differenz $\tau_{\rm max} \ – \tau_{\rm min}$ der Verzögerungszeiten in den beiden Pfaden ist gleich $\tau_0 = 1 \ \rm µ s$.

• Damit ist die Kohärenzbandbreite

$$B_{\rm K}\hspace{0.01cm}' = {1}/{\tau_{\rm 0} } \hspace{0.1cm} \underline {=1\,{\rm MHz}} \hspace{0.05cm}.$$

• Das Ergebnis ist unabhängig von $k_2$. Es gilt für $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ und $k_2 = 10^{-4} \Rightarrow k_0 = 1$ in gleicher Weise.
• In der Grafik ist diese Näherung $B_{\rm K}\hspace{0.01cm}'$ für die Kohärenzbandbreite eingezeichnet.

(6)  Richtig ist der Lösungsvorschlag 2.:

• Der Kanal ist nichtfrequenzselektiv, wenn die Kohärenzbandbreite $B_{\rm K}$ deutlich größer ist als die Signalbandbreite $B_{\rm S}$.
• Dies trifft beim gegebenen Kanal für GSM zu, nicht jedoch für UMTS. Bei UMTS liegt ein frequenzselektiver Kanal vor.