Exercise 3.7: Optimal Nyquist Equalization once again

• Return to book

Transversalfilterfrequenzgang

Wir gehen bei dieser Aufgabe von folgenden Voraussetzungen aus:

• binäre bipolare NRZ–Rechteckimpulse

$$|H_{\rm S}(f)|= {\rm si}(\pi f T) \hspace{0.05cm},$$

• Koaxialkabel mit der Kabeldämpfung  $a_* = 9.2 \ {\rm Np} \ (\approx 80 \ \rm dB)$:

$$|H_{\rm K}(f)|= {\rm e}^{ -9.2 \cdot \sqrt{2 \cdot |f| \cdot T} }\hspace{0.05cm},$$

• optimaler Nyquistentzerrer, bestehend aus Matched–Filter und Transversalfilter:

$$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f)$$

$$\hspace{0.8cm}{\rm mit}\hspace{0.2cm}H_{\rm MF}(f) = H_{\rm S}^{\star}(f) \cdot H_{\rm K}^{\star}(f)\hspace{0.05cm},\hspace{0.2cm} H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}\hspace{0.05cm}.$$

Hierbei bezeichnet  $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$  das Produkt von Sender– und Kanalfrequenzgang.

Wegen der Nyquistentzerrung ist das Auge maximal geöffnet. Für die Fehlerwahrscheinlichkeit gilt:

$$p_{\rm S} \left ( = p_{\rm U} \right ) = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T}{N_0 \cdot \sigma_{d,\hspace{0.05cm} {\rm norm}}^2}} \right ) \hspace{0.05cm}.$$

Die normierte Störleistung am Entscheider ist durch folgende Gleichungen gegeben:

$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \hspace{0.5cm} = \hspace{0.5cm} \sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f \hspace{0.5cm}= \hspace{0.5cm}T \cdot \int_{0}^{1/T} H_{\rm TF}(f) \,{\rm d} f \hspace{0.05cm}.$$

Die Gültigkeit dieser Gleichung ergibt sich aus der Periodizität des Transversalfilterfrequenzgangs  $H_{\rm TF}(f)$.

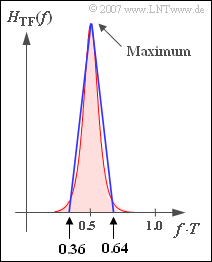
• In der Grafik erkennt man die normierte Störleistung als die rot hinterlegte Fläche.
• Näherungsweise kann die normierte Störleistung durch die in der Grafik blau eingezeichnete Dreieckfläche berechnet werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Linare Nyquistentzerrung.

• Zur Bestimmung der Fehlerwahrscheinlichkeit können Sie das interaktive Berechnungsmodul  Komplementäre Gaußsche Fehlerfunktionen  benutzen.

Fragebogen

1

Berechnen Sie den Betrag des Sender–Kanal–Frequenzgangs für die Frequenzen  $f = 0$,  $f = 1/(2T)= f_{\rm Nyq}$  und  $f = 1/T = 2 \cdot f_{\rm Nyq}$.

$|H_{\rm SK} (f = 0)| \hspace{0.8cm} = \ $

$|H_{\rm SK} (f = f_{\rm Nyq})| \hspace{0.2cm} = \ $ $\ \cdot 10^{-5}$

$|H_{\rm SK} (f = 1/T)| \hspace{0.25cm} = \ $

2

Berechnen Sie den Maximalwert von  $H_{\rm TF}(f)$  bei der Frequenz  $f = f_{\rm Nyq}$.

$|H_{\rm TF} (f = f_{\rm Nyq})| \hspace{0.2cm} = \ $ $\ \cdot 10^8$

3

Berechnen Sie die normierte Störleistung entsprechend der Dreiecknäherung.

$\sigma_{d, \ \rm norm}^2 \hspace{0.2cm} = \ $ $\ \cdot 10^7$

4

Welche Symbolfehlerwahrscheinlichkeit ergibt sich mit  $s_0^2 \cdot T/N_0 = 10^8$?

$p_{\rm S} \hspace{0.2cm} = \ $ $\ \%$

Musterlösung

Solution

(1)  Allgemein gilt für alle Frequenzen $f \ge 0$:  

$$|H_{\rm SK}(f)|= {\rm si}(\pi f T) \cdot {\rm e}^{ -9.2 \cdot \sqrt{2 \cdot |f| \cdot T} }\hspace{0.05cm}.$$

• Daraus ergeben sich die gesuchten Sonderfälle:

$$f= 0 \text{:} \ \hspace{0.1cm}|H_{\rm SK}(f = 0)|= {\rm si}(0) \cdot {\rm e}^0 \hspace{0.15cm}\underline {= 1} \hspace{0.05cm},$$

$$f= f_{\rm Nyq}\text{:} \ \hspace{0.1cm}|H_{\rm SK}(f = \frac{1}{2T})|= {\rm si}({\pi}/{2}) \cdot {\rm e}^{-9.2} \hspace{0.15cm}\underline { \approx 6.43 \cdot 10^{-5}} \hspace{0.05cm},$$

$$f= {1}/{T} \text{:}\ \hspace{0.1cm}|H_{\rm SK}(f = \frac{1}{T})|= {\rm si}({\pi}) \cdot {\rm e}^{...} \hspace{0.15cm}\underline { = 0} \hspace{0.05cm}.$$

(2)  Die Grafik zeigt, dass $H_{\rm TF}(f)$ bei $f = f_{\rm Nyq}$ maximal wird. Daraus folgt mit der angegebenen Gleichung, dass

$${\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - \frac{\kappa}{T}) |^2}$$

bei der Nyquistfrequenz minimal ist. Für $f = f_{\rm Nyq}$ tragen von der unendlichen Summe allerdings nur die Terme mit $\kappa = 0$ und $\kappa = 1$ relevant zum Ergebnis bei.

• Daraus folgt weiter mit dem Ergebnis aus (1):

$${\rm Max} \left [ H_{\rm TF}(f) \right ] \ = \ H_{\rm TF}(f = f_{\rm Nyq})= {1}/{2 \cdot |H_{\rm SK}(f = f_{\rm Nyq}) |^2} = \ \frac{1}{2 \cdot (6.43 \cdot 10^{-5})^2}= \frac{10^{10}}{82.69} \hspace{0.15cm}\underline {\approx 1.21 \cdot 10^{8}} \hspace{0.05cm}.$$

(3)  Nähert man das Integral über $H_{\rm TF}(f)$ durch die in der Grafik eingezeichnete Dreieckfläche an, so erhält man:

$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{0}^{1/T} H_{\rm TF}(f) \,{\rm d} f \approx T \cdot \frac{1}{2}\cdot 1.21 \cdot 10^{8}\cdot (0.64 -0.36)\hspace{0.15cm}\underline {\approx 1.7 \cdot 10^{7}} \hspace{0.05cm}.$$

(4)  Gemäß der gegebenen Gleichung erhält man für die (mittlere) Symbolfehlerwahrscheinlichkeit:

$$p_{\rm S} = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T}{N_0 \cdot \sigma_{d,\hspace{0.05cm} {\rm norm}}^2}} \right ) = {\rm Q}\left ( \sqrt{\frac{10^{8}}{1.7 \cdot 10^{7}}} \right ) \approx {\rm Q}(2.42)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm S} \hspace{0.15cm}\underline {\approx 0.8 \%} \hspace{0.05cm}.$$

Da ein Nyquistsystem vorliegt, ist die ungünstigste (worst–case) Fehlerwahrscheinlichkeit $p_{\rm U}$ genau so groß.