Exercise 4.8: Diamond-shaped Joint PDF
From LNTwww
Wir betrachten eine 2D–Zufallsgröße $(x, y)$, deren Komponenten sich jeweils als Linearkombinationen zweier Zufallsgrößen $u$ und $v$ ergeben:
- $$x=2u-2v+1,$$
- $$y=u+3v.$$
Weiter ist zu beachten:
- Die zwei statistisch unabhängigen Zufallsgrößen $u$ und $v$ sind jeweils gleichverteilt zwischen $0$ und $1$.
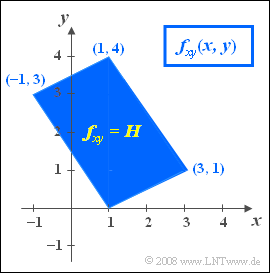
- In der Abbildung sehen Sie die 2D–WDF. Innerhalb des blau eingezeichneten Parallelogramms gilt:
- $$f_{xy}(x, y) = H = {\rm const.}$$
- Außerhalb des Parallelogramms sind keine Werte möglich: $f_{xy}(x, y) = 0$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Linearkombinationen von Zufallsgrößen.
- Bezug genommen wird auch auf die Seite Korrelationsgerade.
- Wir verweisen hier auch auf das interaktive Applet Korrelationskoeffizient und Regressionsgerade.
- Gehen Sie - wenn möglich - von den angegebenen Gleichungen aus. Nutzen Sie die Informationen der obigen Skizze vorwiegend nur zur Kontrolle Ihrer Ergebnisse.
Fragebogen
Musterlösung
(1) Die Fläche des Parallelogramms kann aus zwei gleich großen Dreiecken zusammengesetzt werden.
- Die Fläche des Dreiecks $(1,0)\ (1,4)\ (-1,3)$ ergibt $0.5 · 4 · 2 = 4$.
- Die Gesamtfläche ist doppelt so groß: $F = 8$.
- Da das WDF–Volumen stets $1$ ist, gilt $H= 1/F\hspace{0.15cm}\underline{ = 0.125}$.
(2) Der minimale Wert von $x$ ergibt sich für $\underline{ u=0}$ und $\underline{ v=1}$.
- Daraus folgen aus obigen Gleichungen die Ergebnisse $x= -1$ und $y= +3$.
(3) Die im Theorieteil angegebene Gleichung gilt allgemein, also für jede beliebige WDF der beiden statistisch unabhängigen Größen $u$ und $v$,
- so lange diese gleiche Streuungen aufweisen $(\sigma_u = \sigma_v)$.
- Mit $A = 2$, $B = -2$, $D = 1$ und $E = 3$ erhält man:
- $$\rho_{xy } = \frac {\it A \cdot D + B \cdot E}{\sqrt{(\it A^{\rm 2}+\it B^{\rm 2})(\it D^{\rm 2}+\it E^{\rm 2})}} =\frac {2 \cdot 1 -2 \cdot 3}{\sqrt{(4 +4)(1+9)}} = \frac {-4}{\sqrt{80}} = \frac {-1}{\sqrt{5}}\hspace{0.15cm}\underline{ = -0.447}. $$
(4) Die Korrelationsgerade lautet allgemein:
- $$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x-m_x)+m_y.$$
- Aus den linearen Mittelwerten $m_u = m_v = 0.5$ und den in der Aufgabenstellung angegebenen Gleichungen erhält man $m_x = 1$ und $m_y = 2$.
- Die Varianzen von $u$ und $v$ betragen jeweils $\sigma_u^2 = \sigma_v^2 =1/12$. Daraus folgt:
- $$\sigma_x^2 = 4 \cdot \sigma_u^2 + 4 \cdot \sigma_v^2 = 2/3,$$
- $$\sigma_y^2 = \sigma_u^2 + 9\cdot \sigma_v^2 = 5/6.$$
- Setzt man diese Werte in die Gleichung der Korrelationsgeraden ein, so ergibt sich:
- $$y=K(x)=\frac{\sqrt{5/6}}{\sqrt{2/3}}\cdot (\frac{-1}{\sqrt{5}})\cdot(x-1)+2= - x/{2} + 2.5.$$
- Daraus folgt der Wert $y_0=K(x=0)\hspace{0.15cm}\underline{ = 2.5}$
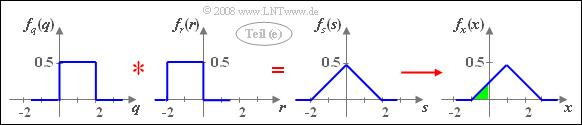
(5) Mit den Hilfsgrößen $q= 2u$, $r= -2v$ und $s= x-1$ gilt der Zusammenhang: $s= q+r$.
- Da $u$ und $v$ jeweils zwischen $0$ und $1$ gleichverteilt sind, besitzt $q$ eine Gleichverteilung im Bereich von $0$ bis $2$ und $r$ ist gleichverteilt zwischen $-2$ und $0$.
- Da zudem $q$ und $r$ nicht statistisch voneinander abhängen, gilt für die WDF der Summe:
- $$f_s(s) = f_q(q) \star f_r(r).$$
- Die Addition $x = s+1$ führt zu einer Verschiebung der Dreieck–WDF um $1$ nach rechts.
- Für die gesuchte Wahrscheinlichkeit (im folgenden Bild grün hinterlegt) gilt deshalb: ${\rm Pr}(x < 0)\hspace{0.15cm}\underline{ = 0.125}$.
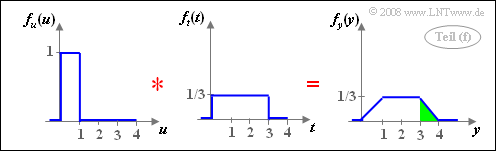
(6) Analog zur Musterlösung für die Teilaufgabe (5) gilt mit $t = 3v$:
- $$f_y(y) = f_u(u) \star f_t(t).$$
- Die Faltung zwischen zwei verschieden breiten Rechtecken ergibt ein Trapez.
- Für die gesuchte Wahrscheinlichkeit erhält man ${\rm Pr}(y>3) =1/6\hspace{0.15cm}\underline{ \approx 0.167}$.
- Diese Wahrscheinlichkeit ist in der rechten Skizze grün hinterlegt.