Exercise 1.5: Reconstruction of the Jakes Spectrum

• Return to book

Considered Jakes spectrum

In a mobile radio system, the  Doppler effect  is also noticeable in the power density spectrum of the Doppler frequency  $f_{\rm D}$ .

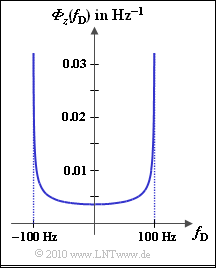
This results in the so-called  Jakes spectrum, which is shown in the graph for the maximum Doppler frequency  $f_{\rm D, \ max} = 100 \ \rm Hz$. ${\it \Phi}_z(f_{\rm D})$  has only portions within the range  $± f_{\rm D, \ max}$, where $${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2} } \hspace{0.05cm}.$$

What is expressed in the frequency domain by the power spectral density (PSD) is described in the time domain by the autocorrelation function (ACF). The ACF is the   ${\it \Phi}_z(f_{\rm D})$  by the  checkLink:_Buch_1 ⇒ inverse Fourier transform of the PSD.

With the Bessel function of the first kind and zero order  $({\rm J}_0)$  you get

$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$

To take into account the Doppler effect and thus a relative movement between transmitter and receiver in a system simulation, two digital filters are inserted in the  Rayleigh channel model, each with the frequency response  $H_{\rm DF}(f_{\rm D})$.

The dimensioning of these filters is part of this task.

• We restrict ourselves here to the branch for generating the real part  $x(t)$. The ratios derived here are also valid for the imaginary part  $y(t)$.
• At the input of the left digital filter of the   Rayleigh channel model , there is white Gaussian noise  $n(t)$  with variance  $\sigma^2 = 0.5$.
• The real component is then obtained from the following convolution

$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$

Notes:

• This task belongs to the subject area  Statistische Bindungen innerhalb des Rayleigh–Prozesses.
• The digital filter is treated in detail in chapter  Digitale Filter  of the book „Stochastic Signal Theory”.

Questions

1

What is the value of the Jakes, spectrum of the real part at the Doppler frequency  $f_{\rm D} = 0$?

${\it \Phi}_x(f_{\rm D} = 0)\ = \ $ $\ \cdot 10^{\rm –3} \ 1/{\rm Hz}$

2

Which dimensioning is correct, where  $K$  is an appropriately chosen constant?

	It holds  $H_{\rm DF}(f_{\rm D}) = K \cdot {\it \Phi}_x(f_{\rm D})$.
	It applies  $|H_{\rm DF}(f_{\rm D})|^2 = K \cdot {\it \Phi}_x(f_{\rm D})$

3

From which condition can the constant  $K$  be determined?

	$K$  can be selected as desired.
	The integral over  $|H_{\rm DF}(f_{\rm D})|$  must equal  $1$ .
	The integral over  $|H_{\rm DF}(f_{\rm D})|^2$  must be  $1$ .

4

Is  $H_{\rm DF}(f)$  unambiguously defined by the two conditions according to (2) and (3)'?

	Yes.
	No.

Solutions

Solution

(1)  The Jakes spectrum of the real part is half the resulting spectrum ${\it \Phi}_z(f)$:

$${\it \Phi}_x(f_{\rm D} = 0) = {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}= \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = \frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} \hspace{0.05cm}.$$

(2)  Solution 2 is correct:

• The input signal $n(t)$ has a white (constant) LDS ${\it \Phi}_n(f_{\rm D})$.
• The PSD at the output is then

$${\it \Phi}_x(f_{\rm D}) = {\it \Phi}_n(f_{\rm D}) \cdot | H_{\rm DF}(f_{\rm D}|^2 \hspace{0.05cm}.$$

(3)  Solution 3 is correct.

• Only if this condition is fulfilled, the signal $x(t)$ has the same variance $\sigma^2$ as the noise signal $n(t)$.

(4)  No:

• The two conditions after subtasks (2) and (3) only refer to the magnitude of the digital filter.
• There is no constraint for the phase of the digital filter.
• This phase can be chosen arbitrarily. Usually it is chosen in such a way that a minimum phase network results.
• In this case, the impulse response $h_{\rm DF}(t)$ then has the lowest possible duration.

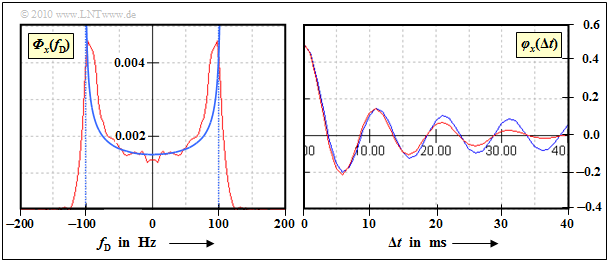
The graph shows the result of the approximation. The red curves were determined simulatively over $100\hspace{0.05cm}000$ samples. You can see:

Approximation of the Jakes spectrum and ACF

• The Jakes power spectral density (left graph) can only be reproduced very inaccurately due to the vertical drop at $± f_{\rm D, \ max}$.
• For the time domain, this means that the ACF decreases much faster than theory suggests.
• For small values of $\delta t$, however, the approximation is very good (right graph).