Augendiagramm und ungünstigste Fehlerwahrscheinlichkeit
Contents
Programmbeschreibung
Das Applet verdeutlicht die Augendiagramme für
- verschiedene Codierungen (binär–redundanzfrei, quaternär–redundanzfrei, pseudo–ternär: AMI und Duobinär) sowie
- verschiedene Empfangskonzepte (Matched–Filter–Empfänger, CRO–Nyquistsystem, gaußförmiges Empfangsfilter).
Das letzte Empfängerkonzept führt zu Impulsinterferenzen, das heißt: Benachbarte Symbole beeinträchtigen sich bei der Symbolentscheidung gegenseitig.
Solche Impulsinterferenzen und deren Einfluss auf die Fehlerwahrscheinlichkeit lassen sich durch das Augendiagramm sehr einfach erfassen und quantifizieren. Aber auch für die beiden anderen (impulsinterferenzfreien) Systeme lassen sich anhand der Grafiken wichtige Erkenntnisse gewinnen.
Ausgegeben wird zudem die ungünstigste („worst case”) Fehlerwahrscheinlichkeit $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$, die bei den binären Nyquistsystemen identisch mit der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$ ist und für die beiden anderen Systemvarianten eine geeignete obere Schranke darstellt: $p_{\rm U} \ge p_{\rm M}$.
In der $p_{\rm U}$–Gleichung bedeuten:
- ${\rm Q}(x)$ ist die Komplementäre Gaußsche Fehlerfunktion. Die normierte Augenöffnung kann Werte zwischen $0 \le ö_{\rm norm} \le 1$ annehmen.
- Der Maximalwert $(ö_{\rm norm} = 1)$ gilt für die binären Nyquistsysteme und $ö_{\rm norm}=0$ steht für ein „geschlossenes Auge”.
- Der normierte Detektionsrauscheffektivwert $\sigma_{\rm norm}$ hängt vom einstellbaren Parameter $10 \cdot \lg \ E_{\rm B}/N_0$ ab, aber auch von der Codierung und vom Empfängerkonzept.
Theoretischer Hintergrund
Systembeschreibung und Voraussetzungen
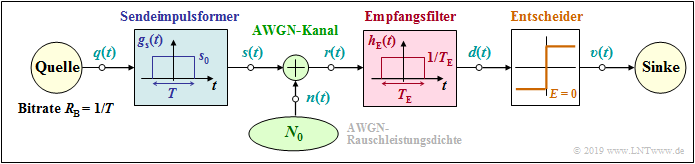
Für dieses Applet gilt das unten skizzierte Modell der binären Basisbandübertragung. Zunächst gelten folgende Voraussetzungen:
- Die Übertragung erfolgt binär, bipolar und redundanzfrei mit der Bitrate $R_{\rm B} = 1/T$, wobei $T$ die Symboldauer angibt.
- Das Sendesignal $s(t)$ ist zu allen Zeiten $t$ gleich $ \pm s_0$ ⇒ Der Sendegrundimpuls $g_s(t)$ ist NRZ–rechteckförmig mit Amplitude $s_0$ und Impulsdauer $T$.
- Das Empfangssignal sei $r(t) = s(t) + n(t)$, wobei der AWGN–Term $n(t)$ durch die (einseitige) Rauschleistungsdichte $N_0$ gekennzeichnet ist.
- Der Kanalfrequenzgang sei bestmöglich (ideal) und muss nicht weiter berücksichtigt werden: $H_{\rm K}(f) =1$.
- Das Empfangsfilter mit der Impulsantwort $h_{\rm E}(t)$ formt aus $r(t)$ das Detektionssignal $d(t) = d_{\rm S}(t)+ d_{\rm N}(t)$.
- Dieses wird vom Entscheider mit der Entscheiderschwelle $E = 0$ zu den äquidistanten Zeiten $\nu \cdot T$ ausgewertet.
- Es wird zwischen dem Signalanteil $d_{\rm S}(t)$ – herrührend von $s(t)$ – und dem Rauschanteil $d_{\rm N}(t)$ unterschieden, dessen Ursache das AWGN–Rauschen $n(t)$ ist.
- $d_{\rm S}(t)$ kann als gewichtete Summe von gewichteten und jeweils um $T$ verschobenen Detektionsgrundimpulsen $g_d(t) = g_s(t) \star h_{\rm E}(t)$ dargestellt werden.
- Zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit benötigt man ferner die Varianz $\sigma_d^2 = {\rm E}\big[d_{\rm N}(t)^2\big]$ des Detektionsrauschanteils (bei AWGN–Rauschen).
Optimales impulsinterferenzfreies System – Matched-Filter-Empfänger
Die minimale Fehlerwahrscheinlichkeit ergibt sich für den hier betrachteten Fall $H_{\rm K}(f) =1$ mit dem Matched-Filter-Empfänger, also dann, wenn $h_{\rm E}(t)$ formgleich mit dem NRZ–Sendegrundimpuls $g_s(t)$ ist. Die rechteckförmige Impulsantwort $h_{\rm E}(t)$ hat dann die Dauer $T_{\rm E} = T$ und die Höhe $1/T$.
- Der Detektionsgrundimpuls $g_d(t)$ ist dreieckförmig mit dem Maximum $s_0$ bei $t=0$ ; es gilt $g_d(t)=0$ für $|t| \ge T$. Aufgrund dieser engen zeitlichen Begrenzung kommt es nicht zu Impulsinterferenzen ⇒ $d_{\rm S}(t = \nu \cdot T) = \pm s_0$ ⇒ der Abstand aller Nutzabtastwerte von der Schwelle $E = 0$ ist stets $|d_{\rm S}(t = \nu \cdot T)| = s_0$.
- Die Detektionsrauschleistung ist bei dieser Konstellation:
- $$\sigma_d^2 = N_0/2 \cdot \int_{-\infty}^{+\infty} |h_{\rm E}(t)|^2 {\rm d}t = N_0/(2T)=\sigma_{\rm MF}^2.$$
- Für die (mittlere) Fehlerwahrscheinlichkeit gilt mit der Komplementären Gaußschen Fehlerfunktion ${\rm Q}(x)$ :
- $$p_{\rm M} = {\rm Q}\left[\sqrt{{s_0^2}/{\sigma_d^2}}\right ] = {\rm Q}\left[\sqrt{{2 \cdot s_0^2 \cdot T}/{N_0}}\right ] = {\rm Q}\left[\sqrt{2 \cdot E_{\rm B}/ N_0}\right ].$$
Das Applet berücksichtigt diesen Fall mit den Einstellungen „nach Spalt–Tiefpass” sowie $T_{\rm E}/T = 1$. Die ausgegebenen Werte sind im Hinblick auf spätere Konstellationen
- die normierte Augenöffnung $ö_{\rm norm} =1$ ⇒ dies ist der maximal mögliche Wert,
- der normierte Detektionsrauscheffektivwert (gleich der Wurzel aus der Detektionsrauschleistung) $\sigma_{\rm norm} =\sqrt{1/(2 \cdot E_{\rm B}/ N_0)}$ sowie
- die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$ ⇒ bei impulsinterferenzfreien Systemen stimmen $p_{\rm M}$ und $p_{\rm U}$ überein.
$\text{Unterschiede bei den Mehrstufensystemen}$
- Es gibt $M\hspace{-0.1cm}-\hspace{-0.1cm}1$ Augen und eben so viele Schwellen ⇒ $ö_{\rm norm} =1/(M\hspace{-0.1cm}-\hspace{-0.1cm}1)$ ⇒ $M=4$: Quaternärsystem, $M=3$: AMI-Code, Duobinärcode.
- Der normierte Detektionsrauscheffektivwert $\sigma_{\rm norm}$ ist beim Quaternärsystem um den Faktor $\sqrt{5/9} \approx 0.745$ kleiner als beim Binärsystem.
- Beim AMI-Code und dem Duobinärcode hat dieser Verbesserungsfaktor, der auf das kleinere $E_{\rm B}/ N_0$ zurückgeht, den Wert $\sqrt{1/2} \approx 0.707$.
Nyquist–System mit Cosinus-Rolloff-Gesamtfrequenzgang
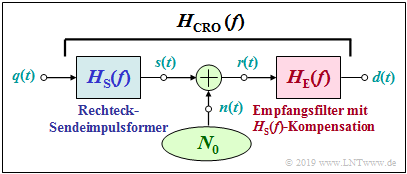
Wir setzen voraus, dass der Gesamtfrequenzgang zwischen der diracförmigen Quelle bis zum Entscheider den Verlauf eines Cosinus-Rolloff-Tiefpasses hat ⇒ $H_{\rm S}(f)\cdot H_{\rm E}(f) = H_{\rm CRO}(f)$ .
- Der Flankenabfall von $H_{\rm CRO}(f)$ ist punktsymmetrisch um die Nyquistfrequenz $1/(2T)$. Je größer der Rolloff-Faktor $r_{ \hspace {-0.05cm}f}$ ist, um so flacher verläuft die Nyquistflanke.
- Der Detektionsgrundimpuls $g_d(t) = s_0 \cdot T \cdot {\mathcal F}^{-1}\big[H_{\rm CRO}(f)\big]$ hat unabhängig von $r_{ \hspace {-0.05cm}f}$ zu den Zeiten $\nu \cdot T$ Nullstellen. Weitere Nulldurchgänge gibt es abhängig von $r_{ \hspace {-0.05cm}f}$. Für den Impuls gilt:
- $$g_d(t) = s_0 \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm si}(\pi \hspace{-0.05cm}\cdot\hspace{-0.05cm} t/T )\hspace{-0.05cm}\cdot\hspace{-0.05cm}\frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot t/T )}{1 - (2 \cdot r_{\hspace{-0.05cm}f} \cdot t/T)^2}.$$
- Daraus folgt: Wie beim Matched-Filter-Empfänger ist das Auge maximal geöffnet ⇒ $ö_{\rm norm} =1$.
Betrachten wir nun die Rauschleistung vor dem Entscheider. Für diese gilt:
- $$\sigma_d^2 = N_0/2 \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 {\rm d}f = N_0/2 \cdot \int_{-\infty}^{+\infty} \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm S}(f)|^2} {\rm d}f.$$
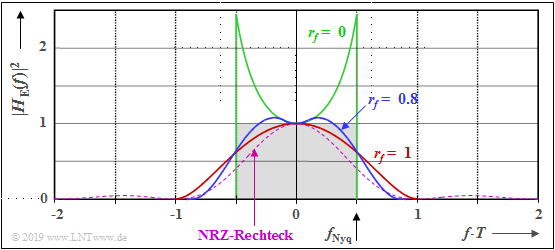
Die Grafik zeigt die Leistungsübertragungsfunktion $|H_{\rm E}(f)|^2$ für drei verschiedene Rolloff–Faktoren
- $r_{ \hspace {-0.05cm}f}=0$ ⇒ grüne Kurve,
- $r_{ \hspace {-0.05cm}f}=1$ ⇒ rote Kurve,
- $r_{ \hspace {-0.05cm}f}=0.8$ ⇒ blaue Kurve.
Die Flächen unter diesen Kurven sind jeweils ein Maß für die Rauschleistung $\sigma_d^2$. Das grau hinterlegte Rechteck markiert den kleinsten Wert $\sigma_d^2 =\sigma_{\rm MF}^2$, der sich auch mit dem Matched-Filter-Empfänger ergeben hat.
Man erkennt aus dieser Darstellung:
- Der Rolloff–Faktor $r_{\hspace{-0.05cm}f} = 0$ (Rechteck–Frequenzgang) führt trotz des sehr schmalen Empfangsfilters zu $\sigma_d^2 =K \cdot \sigma_{\rm MF}^2$ mit $K \approx 1.5$, da $|H_{\rm E}(f)|^2$ mit wachsendem $f$ steil ansteigt. Der Grund für diese Rauschleistungsanhebung ist die Funktion $\rm si^2(\pi f T)$ im Nenner, die zur Kompensation des $|H_{\rm S}(f)|^2$–Abfalls erforderlich ist.
- Da die Fläche unter der roten Kurve kleiner ist als die unter der grünen Kurve, führt $r_{\hspace{-0.05cm}f} = 1$ trotz dopplelt so breitem Spektrum zu einer kleineren Rauschleistung: $K \approx 1.23$. Für $r_{\hspace{-0.05cm}f} \approx 0.8$ ergibt sich noch ein geringfügig besserer Wert. Hierfür erreicht man den bestmöglichen Kompromiss zwischen Bandbreite und Überhöhung.
- Der normierte Detektionsrauscheffektivwert lautet somit für den Rolloff–Faktor $r_{ \hspace {-0.05cm}f}$: $\sigma_{\rm norm} =\sqrt{K(r_f)/(2 \cdot E_{\rm B}/ N_0)}$.
- Auch hier stimmt die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$ exakt mit der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$ überein.
$\text{Unterschiede bei den Mehrstufensystemen}$
Alle Anmerkungen im Abschnitt $2.2$ gelten in gleicher Weise für das „Nyquist–System mit Cosinus-Rolloff-Gesamtfrequenzgang”.
Impulsinterferenzbehaftetes System mit Gauß-Empfangsfilter
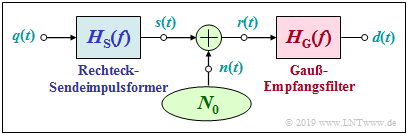
Wir gehen vom rechts skizzierten Blockschaltbild aus. Weiter soll gelten:
- Rechteckförmiger NRZ–Sendegrundimpuls $g_s(t)$ mit der Höhe $s_0$ und der Dauer $T$:
- $$H_{\rm S}(f) = {\rm si}(\pi f T).$$
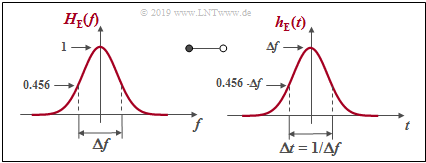
- Gaußförmiges Empfangsfilter mit der Grenzfrequenz $f_{\rm G}$:
- $$H_{\rm E}(f) = H_{\rm G}(f) = {\rm e}^{- \pi \hspace{0.05cm}\cdot \hspace{0.03cm} f^2/(2\hspace{0.05cm}\cdot \hspace{0.03cm}f_{\rm G})^2 } \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm}h_{\rm E}(t) = h_{\rm G}(t) = {\rm e}^{- \pi \cdot (2\hspace{0.05cm}\cdot \hspace{0.03cm} f_{\rm G}\hspace{0.05cm}\cdot \hspace{0.02cm} t)^2} \hspace{0.05cm}.$$
Aufgrund der hier getroffenen Voraussetzungen gilt für den Detektionsgrundimpuls:
- $$g_d(t) = s_0 \cdot T \cdot \big [h_{\rm S}(t) \star h_{\rm G}(t)\big ] = 2 f_{\rm G} \cdot s_0 \cdot \int_{t-T/2}^{t+T/2} {\rm e}^{- \pi \hspace{0.05cm}\cdot\hspace{0.05cm} (2 \hspace{0.05cm}\cdot\hspace{0.02cm} f_{\rm G}\hspace{0.05cm}\cdot\hspace{0.02cm} \tau )^2} \,{\rm d} \tau \hspace{0.05cm}.$$
Die Integration führt zum Ergebnis:
- $$g_d(t) = s_0 \cdot \big [ {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \big ],$$
unter Verwendung der komplementären Gaußschen Fehlerfunktion
- $${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} \hspace{0.05cm}.$$
Das Modul Komplementäre Gaußsche Fehlerfunktionen liefert die Zahlenwerte von ${\rm Q} (x)$.
- Dieser Detektionsgrundimpuls bewirkt Impulsinterferenzen.
- Darunter versteht man, dass die Symbolentscheidung durch die Ausläufer benachbarter Impulse beeinflusst wird. Während bei impulsinterferenzfreien Übertragungssystemen jedes Symbol mit gleicher Wahrscheinlichkeit – nämlich der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$ – verfälscht wird, gibt es günstige Symbolkombinationen mit der Verfälschungswahrscheinlichkeit ${\rm Pr}(v_{\nu} \ne q_{\nu}) < p_{\rm M}$.
- Andere Symbolkombinationen erhöhen dagegen die Verfälschungswahrscheinlichkeit erheblich.
Die Impulsinterferenzen lassen sich durch das sogenannte Augendiagramm sehr einfach erfassen und analysieren. Diese stehen im Mittelpunkt dieses Applets. Alle wichtigen Informationen finden Sie hier.
- Das Augendiagramm entsteht, wenn man alle Abschnitte des Detektionsnutzsignals $d_{\rm S}(t)$ der Länge $2T$ übereinander zeichnet. Die Entstehung können Sie sich im Programm mit „Einzelschritt” verdeutlichen.
- Ein Maß für die Stärke der Impulsinterferenzen ist die vertikale Augenöffnung. Für den symmetrischen Binärfall gilt mit $g_\nu = g_d(\pm \nu \cdot T)$ und geeigneter Normierung:
- $$ ö_{\rm norm} = g_0 -2 \cdot (|g_1| + |g_2| + \text{...}).$$
- Mit größerer Grenzfrequenz stören sich die Impulse weniger und $ ö_{\rm norm}$ nimmt kontinuierlich zu. Gleichzeitig wird bei größerem $f_{\rm G}/R_{\rm B}$ auch der (normierte) Detektionsrauscheffektivwert größer:
- $$ \sigma_{\rm norm} = \sqrt{\frac{f_{\rm G}/R_{\rm B}}{\sqrt{2} \cdot E_{\rm B}/N_{\rm 0}}}.$$
- Die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$ ⇒ „Worst Case” liegt meist deutlich über der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$.
$\text{Unterschiede beim redundanzfreien Quaternärsystem}$
- Für $M=4$ ergeben sich andere Grundimpulswerte.
Beispiel: Mit $M=4, \ f_{\rm G}/R_{\rm B}=0.4$ sind Grundimpulswerte $g_0 = 0.955, \ g_1 = 0.022$ identisch mit $M=2, \ f_{\rm G}/R_{\rm B}=0.8$. - Es gibt nun drei Augenöffnungen und eben so viele Schwellen. Die Gleichung für die normierte Augenöffnung lautet nun: $ ö_{\rm norm} = g_0/3 -2 \cdot (|g_1| + |g_2| + \text{...}).$
- Der normierte Detektionsrauscheffektivwert $\sigma_{\rm norm}$ ist beim Quaternärsystem wieder um den Faktor $\sqrt{5/9} \approx 0.745$ kleiner als beim Binärsystem.
Pseudoternärcodes
Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die Ordnung des Codes. Typisch für eine symbolweise Codierung ist, dass
- die Symboldauer $T$ des Codersignals (und des Sendesignals) mit der Bitdauer $T_{\rm B}$ des binären Quellensignals übereinstimmt, und
- Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.
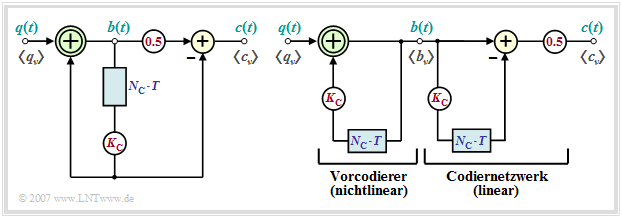
Besondere Bedeutung besitzen Pseudoternärcodes ⇒ Stufenzahl $M = 3$, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist. Genaueres hierzu finden Sie im $\rm LNTwww$–Theorieteil. Fazit:
- Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$:
- $$q_\nu \in \{-1, +1\},\hspace{0.5cm} c_\nu \in \{-1, \ 0, +1\}\hspace{0.05cm}.$$
- Die relative Coderedundanz ist für alle Pseudoternärcodes gleich:
- $$ r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$
Anhand des Codeparameters $K_{\rm C}$ werden verschiedene Pseudoternärcodes erster Ordnung $(N_{\rm C} = 1)$ charakterisiert.
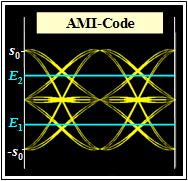
$\Rightarrow \ \ K_{\rm C} = 1\text{: AMI–Code}$ (von: Alternate Mark Inversion)
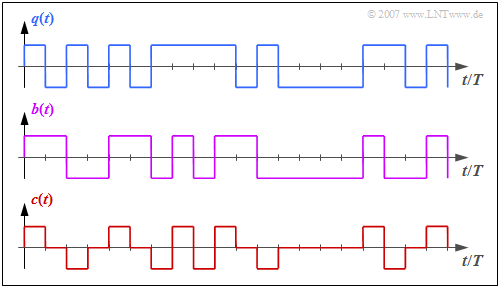
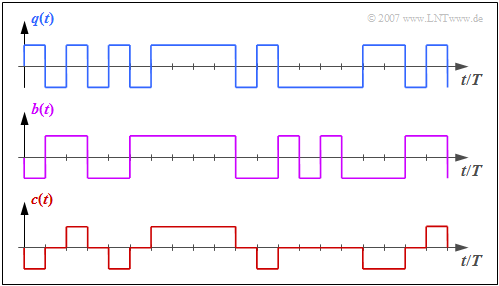
Die Grafik zeigt oben das binäre Quellensignal $q(t)$. Darunter sind dargestellt:
- das ebenfalls binäre Signal $b(t)$ nach dem Vorcodierer, und
- das Codersignal $c(t) = s(t)$ des AMI–Codes.
Man erkennt das einfache AMI–Codierprinzip:
- Jeder Binärwert „–1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Amplitudenkoeffizienten $a_\nu = 0$ codiert.
- Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt.
Damit wird sichergestellt, dass im AMI–codierten Signal keine langen „+1”– bzw. „–1”–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal problematisch wäre.
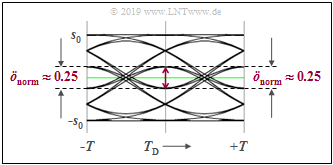
Links ist das Augendiagramm dargestellt.
- Es gibt zwei Augenöffnungen und zwei Schwellen.
- Die normierte Augenöffnung ist $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1)$, wobei $g_0 = g_d(t=0)$ den Hauptwert des Detektionsgrundimpulses bezeichnet und $g_1 = g_d(t=\pm T)$ die relevanten Vor- und Nachläufer, die das Auge vertikal begrenzen.
- Die normierte Augenöffnung ist somit deutlich kleiner als beim vergleichbaren Binäsystem ⇒ $ö_{\rm norm}= g_0 -2 \cdot g_1$.
- Der normierte Rauscheffektivwert $\sigma_{\rm norm}$ ist um den Faktor $\sqrt{1/2} \approx 0.707$ kleiner als beim vergleichbaren Binäsystem.
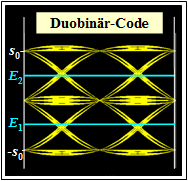
$\Rightarrow \ \ K_{\rm C} = -1\text{: Duobinärcode}$
Aus der rechten Grafik mit den Signalverläufen erkennt man:
- Hier können beliebig viele Symbole gleicher Polarität („+1” bzw. „–1”) direkt aufeinanderfolgen ⇒ der Duobinärcode ist nicht gleichsignalfrei.
- Dagegen tritt beim Duobinärcode die alternierende Folge „ ... , +1, –1, +1, –1, +1, ... ” nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist.
- Auch die Duobinärcode–Folge besteht zu 50% aus Nullen. Der Verbesserungsfaktor durch das kleinere $E_{\rm B}/ N_0$ ist wie beim AMI-Code gleich $\sqrt{1/2} \approx 0.707$.
Links ist das Augendiagramm dargestellt.
- Es gibt wieder zwei „Augen” und zwei Schwellen.
- Die Augenöffnung ist $ö_{\rm norm}= 1/2 \cdot (g_0 - g_1)$.
- $ö_{\rm norm}$ ist also größer als beim AMI–Code und auch wie beim vergleichbaren Binäsystem.
- Nachteilig gegenüber dem AMI–Code ist allerdings, dass er nicht gleichsignalfrei ist.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
(1) Verdeutlichen Sie sich die Entstehung des Augendiagramms für $M=2 \text{, nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$. Wählen Sie hierfür „Einzelschritt”.
- Dieses Augendiagramm ergibt sich, wenn man das Detektionsnutzsignal $d_{\rm S}(t)$ in Stücke der Dauer $2T$ unterteilt und diese Teile übereinander zeichnet.
- In $d_{\rm S}(t)$ müssen alle „Fünf–Bit–Kombinationen” enthalten sein ⇒ mindestens $2^5 = 32$ Teilstücke ⇒ maximal $32$ unterscheidbare Linien.
- Das Diagramm bewertet das Einschwingverhalten des Nutzsignals. Je größer die (normierte) Augenöffnung ist, desto weniger Impulsinterferenzen gibt es.
(2) Gleiche Einstellung wie in (1). Zusätzlich gilt $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$. Bewerten Sie die ausgegebenen Größen $ö_{\rm norm}$, $\sigma_{\rm norm}$ und $p_{\rm U}$.
- $ö_{\rm norm}= 0.542$ zeigt an, dass die Symboldetektion durch benachbarte Impulse beeinträchtigt wird. Für impulsinterferenzfreie Binärsysteme gilt $ö_{\rm norm}= 1$.
- Die Augenöffnung kennzeichnet nur das Nutzsignal. Der Rauscheinfluss wird durch $\sigma_{\rm norm}= 0.184$ erfasst. Dieser Wert sollte möglichst klein sein.
- Die Fehlerwahrscheinlichkeit $p_{\rm U} = {\rm Q}(ö_{\rm norm}/\sigma_{\rm norm}\approx 0.16\%)$ bezieht sich allein auf die „ungünstigsten Folgen”, bei „Gauß” z. B. $-1, -1, +1, -1, -1$.
- Andere Folgen werden weniger verfälscht ⇒ die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$ ist (meist) deutlich kleiner als $p_{\rm U}$ (beschreibt den „Worst Case”).
(3) Die letzten Einstellungen bleiben. Mit welchem $f_{\rm G}/R_{\rm B}$–Wert wird die ungünstigste Fehlerwahrscheinlichkeit $p_{\rm U}$ minimal? Auch das Augendiagramm betrachten.
- Der minimale Wert $p_{\rm U, \ min} \approx 0.65 \cdot 10^{-4}$ ergibt sich für $f_{\rm G}/R_{\rm B} \approx 0.8$, und zwar nahezu unabhängig vom eingestellten $10 \cdot \lg \ E_{\rm B}/N_0$.
- Der normierte Rauscheffektivwert steigt zwar gegenüber dem Versuch (2) von $\sigma_{\rm norm}= 0.168$ auf $\sigma_{\rm norm}= 0.238$ an.
- Dies wird aber durch die größere Augenöffnung $ö_{\rm norm}= 0.91$ gegenüber $ö_{\rm norm}= 0.542$ mehr als ausgeglichen $($Vergrößerungsfaktor $\approx 1.68)$.
(4) Für welche Grenzfrequenzen $(f_{\rm G}/R_{\rm B})$ ergibt sich eine völlig unzureichende Fehlerwahrscheinlichkeit $p_{\rm U} \approx 50\%$ ? Auch das Augendiagramm betrachten.
- Für $f_{\rm G}/R_{\rm B}<0.28$ ergibt sich ein geschlossenes Auge $(ö_{\rm norm}= 0)$ und damit eine worst–case Fehlerwahrscheinlichkeit in der Größenordnung von $50\%$.
- Die Entscheidung über ungünstig eingerahmte Bit muss dann zufällig erfolgen, auch bei geringem Rauschen $(10 \cdot \lg \ E_{\rm B}/N_0 = 16 \ {\rm dB})$.
(5) Wählen Sie nun die Einstellungen $M=2 \text{, nach Spalt–TP, }T_{\rm E}/T = 1$, $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ sowie „Auge – Gesamt”. Interpretieren Sie die Ergebnisse.
- Der Detektionsgrundimpuls ist dreieckförmig und das Auge vollständig geöffnet. Die normierte Augenöffnung ist demzufolge $ö_{\rm norm}= 1.$
- Aus $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ folgt $E_{\rm B}/N_0 = 10$ ⇒ $\sigma_{\rm norm} =\sqrt{1/(2\cdot E_{\rm B}/ N_0)} = \sqrt{0.05} \approx 0.224 $ ⇒ $p_{\rm U} = {\rm Q}(4.47) \approx 3.9 \cdot 10^{-6}.$
- Dieser Wert ist um den Faktor $15$ besser als in (3). Aber: Bei $H_{\rm K}(f) \ne 1$ ist der Matched-Filter-Empfänger so nicht anwendbar.
(6) Gleiche Einstellung wie in (5). Variieren Sie nun $T_{\rm E}/T$ im Bereich zwischen $0.5$ und $1.5$. Interpretieren Sie die Ergebnisse.
- Für $T_{\rm E}/T < 1$ gilt weiterhin $ö_{\rm norm}= 1$. Aber $\sigma_{\rm norm}$ wird größer, zum Beispiel $\sigma_{\rm norm} = 0.316$ für $T_{\rm E}/T =0.5$ ⇒ das Filter ist zu breitbandig!
- Für $T_{\rm E}/T > 1$ ergibt sich im Vergleich zu (5) ein kleineres $\sigma_{\rm norm}$. Aber Das Auge ist nicht mehr geöffnet. $T_{\rm E}/T =1.25$: $ö_{\rm norm}= g_0 - 2 \cdot g_1 = 0.6$.
(7) Wählen Sie nun die Einstellungen $M=2 \text{, CRO–Nyquist, }r_f = 0.2$ sowie „Auge – Gesamt”. Interpretieren Sie das Augendiagramm, auch für andere $r_f$–Werte.
- Im Gegensatz zu (6) ist hier der Grundimpuls für $|t|>T$ nicht Null, aber $g_d(t)$ hat äquidistane Nulldurchgänge: $g_0 = 1, \ g_1 = g_2 = 0$ ⇒ Nyquistsystem.
- Alle $32$ Augenlinien gehen bei $t=0$ durch nur zwei Punkte. Die vertikale Augenöffnung ist für alle $r_f$ maximal ⇒ $ö_{\rm norm}= 1$.
- Dagegen nimmt die horizontale Augenöffnung mit $r_f$ zu und ist $r_f = 1$ maximal gleich $T$ ⇒ Phasenjitter hat in diesem Fall nur geringen Einfluss.
(8) Gleiche Einstellung wie in (7). Variieren Sie nun $r_f$ im Hinblick auf minimale Fehlerwahrscheinlichkeit. Interpretieren Sie die Ergebnisse.
- $ö_{\rm norm}= 1$ gilt stets. Dagegen zeigt $\sigma_{\rm norm}$ eine leichte Abhängigkeit von $r_f$. DasMinimum $\sigma_{\rm norm}=0.236$ ergibt sich für $r_f = 0.9$ ⇒ $p_{\rm U} \approx 1.1 \cdot 10^{-5}.$
- Gegenüber dem bestmöglichen Fall gemäß (7) „Matched–Filter–Empfänger” ist $p_{\rm U}$ dreimal so groß, obwohl $\sigma_{\rm norm}$ nur um ca. $5\%$ größer ist.
- Der größere $\sigma_{\rm norm}$–Wert geht auf die Überhöhung des Rausch–LDS zurück, um den Abfall durch den Sender–Frequenzgang $H_{\rm S}(f)$ auszugleichen.
(9) Wählen Sie die Einstellungen $M=4 \text{, nach Spalt–TP, }T_{\rm E}/T = 1$, $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ und $12 \ {\rm dB}$. Interpretieren Sie die Ergebnisse.
- Es gibt nun drei Augenöffnungen. Gegenüber (5) ist also $ö_{\rm norm}$ um den Faktor $3$ kleiner, $\sigma_{\rm norm}$ dagegen nur um etwa den Faktor $\sqrt{5/9)} \approx 0.75$.
- Für $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ ergibt sich nun die Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2.27\%$ und für $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$ nur mehr $0.59\%$.
(10) Für die restlichen Aufgaben gelte stets $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Betrachten Sie das Augendiagramm für $M=4 \text{, CRO–Nyquist, }r_f = 0.5$.
- In $d_{\rm S}(t)$ müssen alle „Fünf–Symbol–Kombinationen” enthalten sein ⇒ mindestens $4^5 = 1024$ Teilstücke ⇒ maximal $1024$ unterscheidbare Linien.
- Alle $1024$ Augenlinien gehen bei $t=0$ durch nur vier Punkte: $ö_{\rm norm}= 0.333$. $\sigma_{\rm norm} = 0.143$ ist etwas größer als in (9) ⇒ ebenso $p_{\rm U} \approx 1\%$.
(11) Wählen Sie die Einstellungen $M=4 \text{, nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ und variieren Sie $f_{\rm G}/R_{\rm B}$. Interpretieren Sie die Ergebnisse.
- $f_{\rm G}/R_{\rm B}=0.48$ führt zur minimalen Fehlerwahrscheinlichkeit $p_{\rm U} \approx 0.21\%$. Kompromiss zwischen $ö_{\rm norm}= 0.312$ und $\sigma_{\rm norm}= 0.109$.
- Bei zu kleiner Grenzfrequenz dominieren die Impulsinterferenzen. Beispiel: $f_{\rm G}/R_{\rm B}= 0.3$: $ö_{\rm norm}= 0.157; $ $\sigma_{\rm norm}= 0.086$ ⇒ $p_{\rm U} \approx 3.5\%$.
- Bei zu großer Grenzfrequenz dominiert das Rauschen. Beispiel: $f_{\rm G}/R_{\rm B}= 1.0$: $ö_{\rm norm}= 0.333; $ $\sigma_{\rm norm}= 0.157$ ⇒ $p_{\rm U} \approx 1.7\%$.
- Aus dem Vergleich mit (9) erkennt man: Bei Quaternärcodierung ist es günstiger, Impulsinterferenzen zuzulassen.
(12) Welche Unterschiede zeigt das Auge für $M=3 \text{ (AMI-Code), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ gegenüber dem vergleichbaren Binärsystem? Interpretation.
- Der Detektionsgrundimpuls $g_d(t)$ ist in beiden Fällen gleich. Die Abtastwerte sind jeweils $g_0 = 0.771, \ g_1 = 0.114$.
- Beim AMI–Code gibt es zwei Augenöffnungen mit je $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1) = 0.214$. Beim Binärcode: $ö_{\rm norm}= g_0 -2 \cdot g_1 = 0.543$.
- Die AMI–Folge besteht zu 50% aus Nullen. Die Symbole $+1$ und $-1$ wechseln sich ab ⇒ es gibt keine lange $+1$–Folge und keine lange $-1$–Folge.
- Darin liegt der einzige Vorteil des AMI–Codes: Dieser kann auch bei einem gleichsignalfreien Kanal ⇒ $H_{\rm K}(f= 0)=0$ angewendet werden.
(13) Gleiche Einstellung wie in (12), zudem $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Analysieren Sie die Fehlerwahrscheinlichkeit des AMI–Codes.
- Trotz kleinerem $\sigma_{\rm norm} = 0.103$ hat der AMI–Code eine höhere Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2\%$ als der Binärcode: $\sigma_{\rm norm} = 0.146, \ p_{\rm U} \approx \cdot 10^{-4}.$
- Für $f_{\rm G}/R_{\rm B}<0.34$ ergibt sich ein geschlossenes Auge $(ö_{\rm norm}= 0)$ ⇒ $p_{\rm U} =50\%$. Beim Binärcode: Für $f_{\rm G}/R_{\rm B}>0.34$ ist das Auge geöffnet.
(14) Welche Unterschiede zeigt das Auge für $M=3 \text{ (Duobinärcode), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.30$ gegenüber dem vergleichbaren Binärsystem?
- Redundanzfreier Binärcode: $ö_{\rm norm}= 0.096, \ \sigma_{\rm norm} = 0.116 \ p_{\rm U} \approx 20\% $ Duobinärcode: $ö_{\rm norm}= 0.167, \ \sigma_{\rm norm} = 0.082 \ p_{\rm U} \approx 2\% $.
- Insbesondere bei kleinem $f_{\rm G}/R_{\rm B}$ liefert der Duobinärcode gute Ergebnisse, da die Übergänge von $+1$ nach $-1$ (und umgekehrt) im Auge fehlen.
- Selbst mit $f_{\rm G}/R_{\rm B}=0.2$ ist das Auge noch geöffnet. Im Gegensatz zum AMI–Code ist aber „Duobinär” bei gleichsignalfreiem Kanal nicht anwendbar.
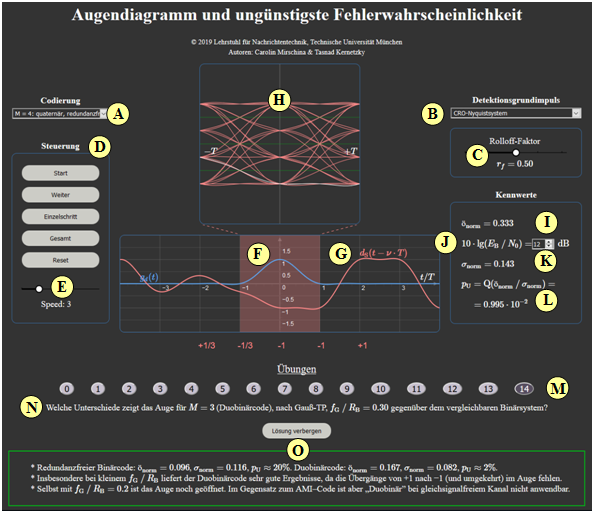
Zur Handhabung des Applets
(A) Auswahl: Codierung
(binär, quaternär, AMI–Code, Duobinärcode)
(B) Auswahl: Detektionsgrundimpuls
(nach Gauß–TP, CRO–Nyquist, nach Spalt–TP}
(C) Prametereingabe zu (B)
(Grenzfrequenz, Rolloff–Faktor, Rechteckdauer)
(D) Steuerung der Augendiagrammdarstellung
(Start, Pause/Weiter, Einzelschritt, Gesamt, Reset)
(E) Geschwindigkeit der Augendiagrammdarstellung
(F) Darstellung: Detektionsgrundimpuls $g_d(t)$
(G) Darstellung: Detektionsnutzsignal $d_{\rm S}(t - \nu \cdot T)$
(H) Darstellung: Augendiagramm im Bereich $\pm T$
( I ) Numerikausgabe: $ö_{\rm norm}$ (normierte Augenöffnung)
(J) Prametereingabe $10 \cdot \lg \ E_{\rm B}/N_0$ für (K)
(K) Numerikausgabe: $\sigma_{\rm norm}$ (normierter Rauscheffektivwert)
(L) Numerikausgabe: $p_{\rm U}$ (ungünstigste Fehlerwahrscheinlichkeit)
(M) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(N) Bereich für die Versuchsdurchführung: Aufgabenstellung
(O) Bereich für die Versuchsdurchführung: Musterlösung einblenden
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2008 von Thomas Großer im Rahmen einer Werkstudententätigkeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.