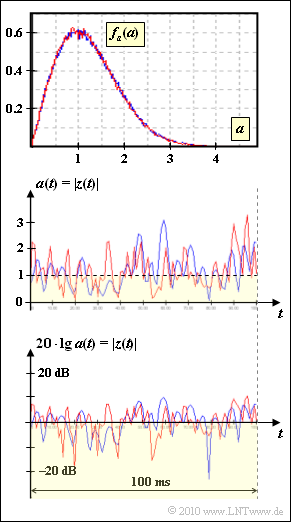
Exercise 1.4: Rayleigh PDF and Jakes PDS

PDF and $|z(t)|$ for Rayleigh Fading with Doppler effect

We consider two different mobile radio channels with Rayleigh fading. In both cases the PDF of the magnitude $a(t) = |z(t)| ≥ 0$ is

$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.05cm}.$$

The probability that this amount is not greater than a given value $A$ is

$${\rm Pr}(|z(t)| \le A) = 1 - {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$

The two channels, which are designated according to the colors „Red” and „Blue” in the graphs with $\rm R$ and $\rm B$ respectively, differ in the speed $v$ and thus in the form of the power density spectrum (PSD) ${\it \Phi}_z(f_{\rm D})$.

In both cases, however, the PSD is a Jakes spectrum.

For a Doppler frequency $f_{\rm D}$ with $|f_{\rm D}| <f_{\rm D,\hspace{0.05cm}max}$ the Jakes spectrum is given by

$${\it \pi}_z(f_{\rm D}) = \frac{1}{\pi \hspace{-0.05cm}\cdot \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt{ 1 \hspace{-0.05cm}- \hspace{-0.05cm}(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2} } \hspace{0.05cm}.$$

For Doppler frequencies outside this interval from $-f_{\rm D,\hspace{0.05cm}max}$ to $+f_{\rm D,\hspace{0.05cm}max}$, we have ${\it \pi}_z(f_{\rm D})=0$.

The corresponding descriptor in the time domain is the autocorrelation function (ACF):

$$\varphi_z ({\rm \delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \delta}t)\hspace{0.05cm}.$$

Here, ${\rm J_0}(.)$ is the Bessel function of the first kind and zeroth order. We have ${\rm J_0}(0) = 1$.
The maximum Doppler frequency of the channel model $\rm R$ : is known to be $f_{\rm D,\hspace{0.05cm}max} = 200 \ \rm Hz$.
It is also known that the speeds $v_{\rm R}$ and $v_{\rm B}$ differ by the factor $2$ .
Whether $v_{\rm R}$ is twice as large as $v_{\rm B}$ or vice versa, you should decide based on the above graphs.

Notes:

This task belongs to the topic of Statistical bindings within the Rayleigh process.
To check your results you can use the interactive applet PDF, CDF and Moments of Special Distributions.

Questionns

Solutions

Solution

(1) The maximum value of the PDF for both channels is $0.6$ and occurs at $a = 1$.

The Rayleigh PDF and its derivative are

$$f_a(a) \hspace{-0.1cm} = \hspace{-0.1cm} \frac{a}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm},$$

$$\frac{{\rm d}f_a(a)}{{\rm d}a} \hspace{-0.1cm} = \hspace{-0.1cm} \frac{1}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)}- \frac{a^2}{\sigma^4} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm}.$$

By setting the derivative to $0$, you can show that the maximum of the PDF occurs at $a = \sigma$. Since the Rayleigh PDF applies to both channels, it follows that

$$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$

(2) As they fading coefficients have the same PDF, the desired probability is also the same for both channels.

Using the given equation, we have

$${\rm Pr}(a \le 0.316) = {\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a \le -10\,\,{\rm dB}) = 1 - {\rm e}^{ -{0.316^2}/(2\sigma^2)} = 1- 0.951 \hspace{0.15cm} \underline{ \approx 4.9 \%} \hspace{0.05cm}.$$

(3) The correct solutions are 2, 3 and 6:

The smaller speed $v_{\rm B}$ can be recognized by the fact that the magnitude $|z(t)|$ changes more slowly with the blue curve.
When the vehicle is stationary, the PSD degenerates to ${\it \Phi_z}(f_{\rm D}) = 2\sigma^2\cdot \delta(f_{\rm D})$, and we have $|z(t)| = A = \rm const.$, where the constant $A$ is drawn from the Rayleigh distribution.
At extremely high speed, the Jakes spectrum becomes flat and has an increasingly smaller magnitude over an increasingly wide range. It then approaches the PSD of white noise. However, $v$ would have to be in the order of the speed of light.

(4) Statements 2 and 3 are correct:

The Rayleigh parameter $\sigma = 1$ also determines the „power” ${\rm E}[|z(t)|^2] = 2\sigma^2 = 2$ of the random process.
This applies to both R and B:

$$\varphi_z ({\rm \delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$

	$v_{\rm B}$ is twice as big as $v_{\rm R}$.
	$v_{\rm B}$ is half as big as $v_{\rm R}$.
	With $v = 0$, $\|z(t)\|$ would be constant.
	With $v = 0$ $\|z(t)\|$ would have a white spectrum.
	With $v → ∞$ $\|z(t)\|$ would be constant.
	With $v → ∞$ $\|z(t)\|$ would be white.

	The PSD value ${\it \Phi_z}(f_{\rm D} = 0)$ is the same for both channels.
	The ACF value $\varphi_z(\Delta t = 0)$ is the same for both channels.
	The area under ${\it \Phi_z}(f_{\rm D})$ is the same for both channels.
	The area below $\varphi_z(\Delta t)$ is the same for both channels.