Exercise 4.3Z: Hilbert Transformator

• Return to book

Hilbert-Transformator

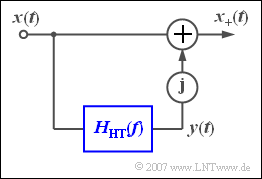
Die Grafik beschreibt ein Modell, wie zumindest gedanklich

• aus dem reellen Bandpass–Signal  $x(t)$
• das analytische Signal  $x_{+}(t)$

generiert werden kann.

Der untere Zweig enthält den so genannten „Hilbert–Transformator” mit dem Frequenzgang  $H_{\rm HT}(f)$. Dessen Ausgangssignal  $y(t)$  wird mit der imaginären Einheit  $\rm j$  multipliziert und zum Signal  $x(t)$  addiert:

$$x_{\rm +}(t)= x(t) + {\rm j}\cdot y(t) .$$

Als Testsignale werden verwendet, jeweils mit  $A = 1 \, \text{V}$  und  $f_0 = 10 \, \text{kHz}$:

$$x_1(t) = A \cdot {\cos} ( 2 \pi f_0 t ),$$

$$x_2(t) = A \cdot {\sin} ( 2 \pi f_0 t ),$$

$$x_3(t) = A \cdot {\cos} \big( 2 \pi f_0 (t - \tau) \big) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}\tau = 12.5 \hspace{0.1cm}{\rm µ s}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Analytisches Signal und zugehörige Spektralfunktion.

• Für die Spektralfunktion des analytischen Signals gilt:

$$ X_{\rm +}(f)= \big[1 + {\rm sign}(f)\big] \cdot X(f).$$

Fragebogen

1

Berechnen Sie den Frequenzgang  $H_{HT}(f)$  des Hilbert-Transformators. Welcher Wert gilt für die Frequenz  $f_0 = 10 \text{ kHz}$?

$\text{Re}[H_{\rm HT}(f = f_0)]\ = \ $

$\text{Im}[H_{\rm HT}(f = f_0)]\ = \ $

2

Wie lautet die Hilbert-Transformierte  $y_1(t)$  für das Eingangssignal  $x_1(t)$? Welcher Wert ergibt sich insbesondere bei  $t = 0$?

$y_1(t = 0)\ = \ $  $\rm V$

3

Wie lautet die Hilbert-Transformierte  $y_2(t)$  für das Eingangssignal  $x_2(t)$? Welcher Wert ergibt sich insbesondere bei  $t = 0$?

$y_2(t = 0)\ = \ $  $\rm V$

4

Wie lautet die Hilbert-Transformierte  $y_3(t)$  für das Eingangssignal  $x_3(t)$? Welcher Wert ergibt sich für  $t=0$?
Wie groß ist die Phasenverzögerung  $\varphi_{\rm HT}$  des Hilbert-Transformators?

$\varphi_{\rm HT}\ = \ $  $\text{Grad}$

$y_3(t = 0)\ = \ $  $\text{V}$

5

Wie lautet das zu  $x_3(t)$  gehörige analytische Signal? Welche Werte haben Real– und Imaginärteil dieses komplexen Signals zum Zeitpunkt  $t = 0$?

$\text{Re}[x_{3+}(t = 0)]\ = \ $  $\text{V}$

$\text{Im}[x_{3+}(t = 0)]\ = \ $  $\text{V}$

Musterlösung

Solution

(1)  Für die Spektralfunktion am Modellausgang gilt:

$$X_{\rm +}(f)= \left(1 + {\rm j}\cdot H_{\rm HT}(f)\right) \cdot X(f).$$

• Ein Vergleich mit der angegebenen Beziehung

$$X_{\rm +}(f)= \left(1 + {\rm sign}(f)\right) \cdot X(f)$$

zeigt, dass  $H_{\rm HT}(f) = - {\rm j} \cdot \sign(f)$  ist.

• Der gesuchte Realteil ist somit  ${\rm Re}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=0}$  und der Imaginärteil ist gleich  ${\rm Im}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=-1}$.

(2)  Aus der Spektralfunktion

$$X_1(f) = {A}/{2}\cdot\delta (f + f_{0})+ {A}/{2}\cdot\delta (f - f_{0}).$$

wird nach dem Hilbert-Transformator:

$$Y_1(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm j}\cdot {A}/{2}\cdot\delta (f - f_{0}).$$

• Damit lautet das Signal am Ausgang des Hilbert-Transformators:

$$y_1(t) = A \cdot {\sin} ( 2 \pi f_0 t ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}y_1(t=0)\hspace{0.15 cm}\underline{ =0}.$$

(3)  Nun lauten die Spektralfunktionen am Eingang und Ausgang des Hilbert-Transformators:

$$X_2(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm j}\cdot {A}/{2}\cdot\delta (f - f_{0}),$$

$$Y_2(f) = -{A}/{2}\cdot\delta (f + f_{0})- {A}/{2}\cdot\delta (f - f_{0}).$$

• Daraus folgt $y_2(t) = - A \cdot \cos(2\pi f_0 t)$ und $y_2(t = 0)\; \underline{= -\hspace{-0.08cm}1 \,\text{V}}$.

(4)  Dieses Eingangssignal lässt sich auch wie folgt darstellen:

$$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot {\rm 0.0125 \hspace{0.05cm} ms}) = A \cdot {\cos} ( 2 \pi f_0 t - \pi/4)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 3\pi/4).$$

• Die Signalphase ist somit  $\varphi = \pi /4$.
• Durch den Hilbert-Transformator wird diese um  $\varphi_{\rm HT} \; \underline{= 90^\circ} \; (\pi /2)$  verzögert.
• Deshalb ist das Ausgangssignal  $y_3(t) = A \cdot \cos(2\pi f_0 t -3 \pi /4)$  und der Signalwert zur Zeit  $t = 0$  beträgt  $A \cdot \cos(135^\circ) \; \underline{= -0.707 \,\text{V}}$.

(5)  Die Spektralfunktion des Signals  $x_3(t)$  lautet:

$$X_3(f) = {A_0}/{2} \cdot {\rm e}^{{\rm j} \varphi}\cdot\delta (f + f_{\rm 0}) + {A_0}/{2} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm 0}) .$$

• Beim analytischen Signal verschwindet der erste Anteil und der Anteil bei  $+f_0$  wird verdoppelt:

$$X_{3+}(f) = {A_0} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm 0}) .$$

• Durch Anwendung des  Verschiebungssatzes  lautet damit die zugehörige Zeitfunktion mit  $\varphi = \pi /4$:

$$x_{3+}(t) = A_0 \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$

• Speziell gilt für den Zeitpunkt  $t = 0$:

$$x_{3+}(t = 0) = A_0 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \varphi} = A_0 \cdot{\cos} ( 45^\circ)-{\rm j}\cdot A_0 \cdot{\sin} ( 45^\circ)= \hspace{0.15 cm}\underline{{\rm 0.707 \hspace{0.05cm} V}-{\rm j}\cdot {\rm 0.707 \hspace{0.05cm} V}}.$$

Hinweis:  

• Um von  $x(t)$  zu  $x_+(t)$  zu kommen, muss man nur die Cosinusfunktion durch die komplexe Exponentialfunktion ersetzen.
• Beispielsweise gilt für eine harmonische Schwingung:

$$x(t) = A \cdot {\cos} ( 2 \pi f_0 t -\hspace{0.05cm} \varphi) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{+}(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$