Eye Pattern and Worst-Case Error Probability

Open Applet in a new tab       German Version

Applet Description

The applet illustrates the eye pattern for different encodings 

• binary  (redundancy-free), 
• quaternary  (redundancy-free),
• pseudo–ternary:  (AMI and duobinary) 

and for various reception concepts 

• Matched Filter receiver, 
• CRO Nyquist system, 
• Gaussian low-pass filter.

The last reception concept leads to intersymbol interference, that is:  Neighboring symbols interfere with each other in symbol decision.

Such intersymbol interferences and their influence on the error probability can be captured and quantified very easily by the "eye pattern".  But also for the other two (without intersymbol interference) systems important insights can be gained from the graphs.

Furthermore, the most unfavorable ("worst case") error probability  

$$p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$$

is output, which for binary Nyquist systems is identical to the mean error probability  $p_{\rm M}$  and represents a suitable upper bound for the other system variants:  $p_{\rm U} \ge p_{\rm M}$.

In the  $p_{\rm U}$–equation mean:

• ${\rm Q}(x)$  is the  Complementary Gaussian Error Function.  The normalized eye opening can have values between  $0 \le ö_{\rm norm} \le 1$  .
• The maximum value  $(ö_{\rm norm} = 1)$  applies to the binary Nyquist system and  $ö_{\rm norm}=0$  represents a "closed eye".
• The normalized detection noise rms value  $\sigma_{\rm norm}$  depends on the adjustable parameter  $10 \cdot \lg \ E_{\rm B}/N_0$  but also on the coding and the receiver concept.

Theoretical Background

Systembeschreibung und Voraussetzungen

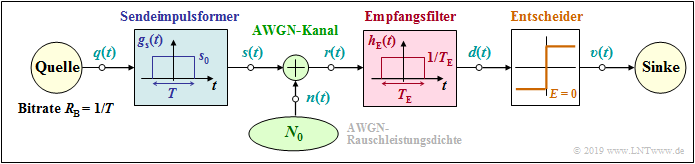
Für dieses Applet gilt das unten skizzierte Modell der binären Basisbandübertragung. Zunächst gelten folgende Voraussetzungen:

• Die Übertragung erfolgt binär, bipolar und redundanzfrei mit der Bitrate  $R_{\rm B} = 1/T$, wobei  $T$  die Symboldauer angibt.
• Das Sendesignal  $s(t)$  ist zu allen Zeiten  $t$  gleich  $\pm s_0$   ⇒   Der Sendegrundimpuls  $g_s(t)$  ist NRZ–rechteckförmig mit Amplitude  $s_0$  und Impulsdauer  $T$.

• Das Empfangssignal sei  $r(t) = s(t) + n(t)$, wobei der AWGN–Term  $n(t)$  durch die (einseitige) Rauschleistungsdichte  $N_0$  gekennzeichnet ist.
• Der Kanalfrequenzgang sei bestmöglich (ideal) und muss nicht weiter berücksichtigt werden:  $H_{\rm K}(f) =1$.
• Das Empfangsfilter mit der Impulsantwort  $h_{\rm E}(t)$  formt aus  $r(t)$  das Detektionssignal  $d(t) = d_{\rm S}(t)+ d_{\rm N}(t)$.
• Dieses wird vom Entscheider mit der Entscheiderschwelle  $E = 0$  zu den äquidistanten Zeiten  $\nu \cdot T$  ausgewertet.
• Es wird zwischen dem Signalanteil  $d_{\rm S}(t)$  – herrührend von  $s(t)$  – und dem Rauschanteil  $d_{\rm N}(t)$  unterschieden, dessen Ursache das AWGN–Rauschen  $n(t)$  ist.
• $d_{\rm S}(t)$  kann als gewichtete Summe von gewichteten und jeweils um  $T$  verschobenen Detektionsgrundimpulsen  $g_d(t) = g_s(t) \star h_{\rm E}(t)$  dargestellt werden.

• Zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit benötigt man ferner die Varianz  $\sigma_d^2 = {\rm E}\big[d_{\rm N}(t)^2\big]$  des Detektionsrauschanteils (bei AWGN–Rauschen).

Optimales impulsinterferenzfreies System – Matched-Filter-Empfänger

Die minimale Fehlerwahrscheinlichkeit ergibt sich für den hier betrachteten Fall  $H_{\rm K}(f) =1$  mit dem Matched-Filter-Empfänger, also dann, wenn  $h_{\rm E}(t)$  formgleich mit dem NRZ–Sendegrundimpuls  $g_s(t)$  ist. Die rechteckförmige Impulsantwort  $h_{\rm E}(t)$  hat dann die Dauer  $T_{\rm E} = T$  und die Höhe  $1/T$.

Binäres Basisbandübertragungssystem;  die Skizze für  $h_{\rm E}(t)$  gilt nur für den Matched-Filter-Empfänger

• Der Detektionsgrundimpuls  $g_d(t)$  ist dreieckförmig mit dem Maximum  $s_0$  bei  $t=0$ ; es gilt  $g_d(t)=0$  für  $|t| \ge T$. Aufgrund dieser engen zeitlichen Begrenzung kommt es nicht zu Impulsinterferenzen   ⇒   $d_{\rm S}(t = \nu \cdot T) = \pm s_0$   ⇒   der Abstand aller Nutzabtastwerte von der Schwelle  $E = 0$  ist stets  $|d_{\rm S}(t = \nu \cdot T)| = s_0$.
• Die Detektionsrauschleistung ist bei dieser Konstellation:

$$\sigma_d^2 = N_0/2 \cdot \int_{-\infty}^{+\infty} |h_{\rm E}(t)|^2 {\rm d}t = N_0/(2T)=\sigma_{\rm MF}^2.$$

• Für die (mittlere) Fehlerwahrscheinlichkeit gilt mit der  Komplementären Gaußschen Fehlerfunktion  ${\rm Q}(x)$ :

$$p_{\rm M} = {\rm Q}\left[\sqrt{{s_0^2}/{\sigma_d^2}}\right ] = {\rm Q}\left[\sqrt{{2 \cdot s_0^2 \cdot T}/{N_0}}\right ] = {\rm Q}\left[\sqrt{2 \cdot E_{\rm B}/ N_0}\right ].$$

Das Applet berücksichtigt diesen Fall mit den Einstellungen  „nach Spalt–Tiefpass”  sowie  $T_{\rm E}/T = 1$. Die ausgegebenen Werte sind im Hinblick auf spätere Konstellationen

• die normierte Augenöffnung  $ö_{\rm norm} =1$   ⇒   dies ist der maximal mögliche Wert,
• der normierte Detektionsrauscheffektivwert (gleich der Wurzel aus der Detektionsrauschleistung)  $\sigma_{\rm norm} =\sqrt{1/(2 \cdot E_{\rm B}/ N_0)}$  sowie
• die ungünstigste Fehlerwahrscheinlichkeit  $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$   ⇒   bei impulsinterferenzfreien Systemen stimmen  $p_{\rm M}$  und   $p_{\rm U}$  überein.

$\text{Unterschiede bei den Mehrstufensystemen}$

• Es gibt  $M\hspace{-0.1cm}-\hspace{-0.1cm}1$ Augen und eben so viele Schwellen   ⇒   $ö_{\rm norm} =1/(M\hspace{-0.1cm}-\hspace{-0.1cm}1)$  ⇒   $M=4$:  Quaternärsystem,  $M=3$:  AMI-Code, Duobinärcode.
• Der normierte Detektionsrauscheffektivwert  $\sigma_{\rm norm}$  ist beim Quaternärsystem um den Faktor  $\sqrt{5/9} \approx 0.745$  kleiner als beim Binärsystem.
• Beim AMI-Code und dem Duobinärcode hat dieser Verbesserungsfaktor, der auf das kleinere  $E_{\rm B}/ N_0$  zurückgeht, den Wert  $\sqrt{1/2} \approx 0.707$.

Nyquist–System mit Cosinus-Rolloff-Gesamtfrequenzgang

Cosinus-Rolloff-Gesamtfrequenzgang

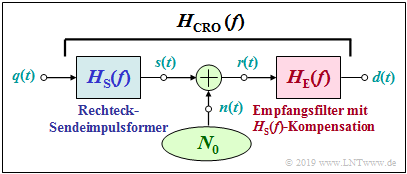
Wir setzen voraus, dass der Gesamtfrequenzgang zwischen der diracförmigen Quelle bis zum Entscheider den Verlauf eines  Cosinus-Rolloff-Tiefpasses  hat   ⇒   $H_{\rm S}(f)\cdot H_{\rm E}(f) = H_{\rm CRO}(f)$ .

• Der Flankenabfall von  $H_{\rm CRO}(f)$  ist punktsymmetrisch um die Nyquistfrequenz  $1/(2T)$. Je größer der Rolloff-Faktor  $r_{ \hspace {-0.05cm}f}$  ist, um so flacher verläuft die Nyquistflanke.
• Der Detektionsgrundimpuls  $g_d(t) = s_0 \cdot T \cdot {\mathcal F}^{-1}\big[H_{\rm CRO}(f)\big]$  hat unabhängig von  $r_{ \hspace {-0.05cm}f}$  zu den Zeiten  $\nu \cdot T$  Nullstellen.  Weitere Nulldurchgänge gibt es abhängig von  $r_{ \hspace {-0.05cm}f}$.  Für den Impuls gilt:

$$g_d(t) = s_0 \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm si}(\pi \hspace{-0.05cm}\cdot\hspace{-0.05cm} t/T )\hspace{-0.05cm}\cdot\hspace{-0.05cm}\frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot t/T )}{1 - (2 \cdot r_{\hspace{-0.05cm}f} \cdot t/T)^2}.$$

• Daraus folgt:  Wie beim Matched-Filter-Empfänger ist das Auge maximal geöffnet   ⇒   $ö_{\rm norm} =1$.

Zur Optimierung des Rolloff-Faktors

Betrachten wir nun die Rauschleistung vor dem Entscheider. Für diese gilt:

$$\sigma_d^2 = N_0/2 \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 {\rm d}f = N_0/2 \cdot \int_{-\infty}^{+\infty} \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm S}(f)|^2} {\rm d}f.$$

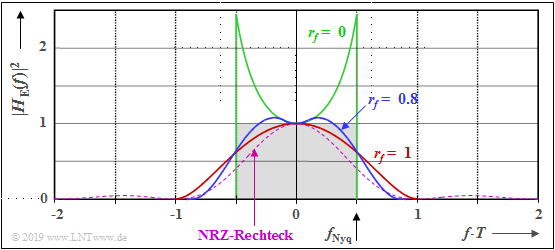
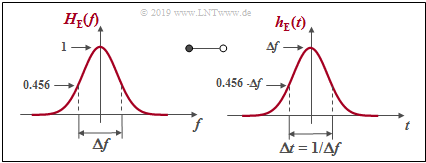
Die Grafik zeigt die Leistungsübertragungsfunktion  $|H_{\rm E}(f)|^2$  für drei verschiedene Rolloff–Faktoren

• $r_{ \hspace {-0.05cm}f}=0$   ⇒   grüne Kurve,
• $r_{ \hspace {-0.05cm}f}=1$   ⇒   rote Kurve,
• $r_{ \hspace {-0.05cm}f}=0.8$   ⇒   blaue Kurve.

Die Flächen unter diesen Kurven sind jeweils ein Maß für die Rauschleistung  $\sigma_d^2$.  Das grau hinterlegte Rechteck markiert den kleinsten Wert  $\sigma_d^2 =\sigma_{\rm MF}^2$, der sich auch mit dem Matched-Filter-Empfänger ergeben hat.
Man erkennt aus dieser Darstellung:

• Der Rolloff–Faktor  $r_{\hspace{-0.05cm}f} = 0$  (Rechteck–Frequenzgang) führt trotz des sehr schmalen Empfangsfilters zu  $\sigma_d^2 =K \cdot \sigma_{\rm MF}^2$  mit  $K \approx 1.5$, da  $|H_{\rm E}(f)|^2$  mit wachsendem  $f$  steil ansteigt. Der Grund für diese Rauschleistungsanhebung ist die Funktion  $\rm si^2(\pi f T)$  im Nenner, die zur Kompensation des  $|H_{\rm S}(f)|^2$–Abfalls erforderlich ist.
  
• Da die Fläche unter der roten Kurve kleiner ist als die unter der grünen Kurve, führt  $r_{\hspace{-0.05cm}f} = 1$  trotz dopplelt so breitem Spektrum zu einer kleineren Rauschleistung:  $K \approx 1.23$.  Für  $r_{\hspace{-0.05cm}f} \approx 0.8$ ergibt sich noch ein geringfügig besserer Wert. Hierfür erreicht man den bestmöglichen Kompromiss zwischen Bandbreite und Überhöhung.
• Der normierte Detektionsrauscheffektivwert lautet somit für den Rolloff–Faktor  $r_{ \hspace {-0.05cm}f}$:   $\sigma_{\rm norm} =\sqrt{K(r_f)/(2 \cdot E_{\rm B}/ N_0)}$.
  
• Auch hier stimmt die ungünstigste Fehlerwahrscheinlichkeit  $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$   exakt mit der mittleren Fehlerwahrscheinlichkeit  $p_{\rm M}$  überein.

$\text{Unterschiede bei den Mehrstufensystemen}$

Alle Anmerkungen im Abschnitt $2.2$ gelten in gleicher Weise für das „Nyquist–System mit Cosinus-Rolloff-Gesamtfrequenzgang”.

Impulsinterferenzbehaftetes System mit Gauß-Empfangsfilter

System mit gaußförmigem Empfangsfilter

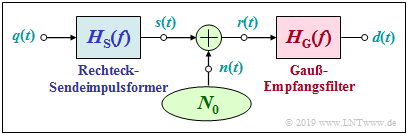
Wir gehen vom rechts skizzierten Blockschaltbild aus. Weiter soll gelten:

• Rechteckförmiger NRZ–Sendegrundimpuls  $g_s(t)$  mit der Höhe  $s_0$  und der Dauer  $T$:

$$H_{\rm S}(f) = {\rm si}(\pi f T).$$

• Gaußförmiges Empfangsfilter mit der Grenzfrequenz  $f_{\rm G}$:

$$H_{\rm E}(f) = H_{\rm G}(f) = {\rm e}^{- \pi \hspace{0.05cm}\cdot \hspace{0.03cm} f^2/(2\hspace{0.05cm}\cdot \hspace{0.03cm}f_{\rm G})^2 } \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm}h_{\rm E}(t) = h_{\rm G}(t) = {\rm e}^{- \pi \cdot (2\hspace{0.05cm}\cdot \hspace{0.03cm} f_{\rm G}\hspace{0.05cm}\cdot \hspace{0.02cm} t)^2} \hspace{0.05cm}.$$

Aufgrund der hier getroffenen Voraussetzungen gilt für den Detektionsgrundimpuls:

Frequenzgang und Impulsantwort des Empfangsfilters

$$g_d(t) = s_0 \cdot T \cdot \big [h_{\rm S}(t) \star h_{\rm G}(t)\big ] = 2 f_{\rm G} \cdot s_0 \cdot \int_{t-T/2}^{t+T/2} {\rm e}^{- \pi \hspace{0.05cm}\cdot\hspace{0.05cm} (2 \hspace{0.05cm}\cdot\hspace{0.02cm} f_{\rm G}\hspace{0.05cm}\cdot\hspace{0.02cm} \tau )^2} \,{\rm d} \tau \hspace{0.05cm}.$$

Die Integration führt zum Ergebnis:

$$g_d(t) = s_0 \cdot \big [ {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t - {T}/{2})\right )- {\rm Q} \left ( 2 \cdot \sqrt {2 \pi} \cdot f_{\rm G}\cdot ( t + {T}/{2} )\right ) \big ],$$

unter Verwendung der komplementären Gaußschen Fehlerfunktion

$${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d {\it u} \hspace{0.05cm}.$$

Das Modul  Komplementäre Gaußsche Fehlerfunktionen  liefert die Zahlenwerte von  ${\rm Q} (x)$.

• Dieser Detektionsgrundimpuls bewirkt  Impulsinterferenzen.
• Darunter versteht man, dass die Symbolentscheidung durch die Ausläufer benachbarter Impulse beeinflusst wird. Während bei impulsinterferenzfreien Übertragungssystemen jedes Symbol mit gleicher Wahrscheinlichkeit – nämlich der mittleren Fehlerwahrscheinlichkeit  $p_{\rm M}$  – verfälscht wird, gibt es günstige Symbolkombinationen mit der Verfälschungswahrscheinlichkeit  ${\rm Pr}(v_{\nu} \ne q_{\nu}) < p_{\rm M}$.
• Andere Symbolkombinationen erhöhen dagegen die Verfälschungswahrscheinlichkeit erheblich.

Binäres Auge $($Gaußtiefpass,  $f_{\rm G}/R_{\rm B} = 0.35)$.

Die Impulsinterferenzen lassen sich durch das sogenannte  Augendiagramm  sehr einfach erfassen und analysieren. Diese stehen im Mittelpunkt dieses Applets. Alle wichtigen Informationen finden Sie  hier.

• Das Augendiagramm entsteht, wenn man alle Abschnitte des Detektionsnutzsignals  $d_{\rm S}(t)$  der Länge  $2T$  übereinander zeichnet. Die Entstehung können Sie sich im Programm mit „Einzelschritt” verdeutlichen.

• Ein Maß für die Stärke der Impulsinterferenzen ist die vertikale Augenöffnung. Für den symmetrischen Binärfall gilt mit  $g_\nu = g_d(\pm \nu \cdot T)$  und geeigneter Normierung:

$$ö_{\rm norm} = g_0 -2 \cdot (|g_1| + |g_2| + \text{...}).$$

• Mit größerer Grenzfrequenz stören sich die Impulse weniger und  $ö_{\rm norm}$  nimmt kontinuierlich zu. Gleichzeitig wird bei größerem  $f_{\rm G}/R_{\rm B}$  auch der (normierte) Detektionsrauscheffektivwert größer:

$$\sigma_{\rm norm} = \sqrt{\frac{f_{\rm G}/R_{\rm B}}{\sqrt{2} \cdot E_{\rm B}/N_{\rm 0}}}.$$

• Die ungünstigste Fehlerwahrscheinlichkeit  $p_{\rm U} = {\rm Q}\left[ö_{\rm norm}/\sigma_{\rm norm} \right ]$   ⇒   „Worst Case” liegt meist deutlich über der mittleren Fehlerwahrscheinlichkeit  $p_{\rm M}$.

$\text{Unterschiede beim redundanzfreien Quaternärsystem}$

• Für  $M=4$  ergeben sich andere Grundimpulswerte.
  Beispiel:     Mit  $M=4, \ f_{\rm G}/R_{\rm B}=0.4$  sind Grundimpulswerte  $g_0 = 0.955, \ g_1 = 0.022$  identisch mit  $M=2, \ f_{\rm G}/R_{\rm B}=0.8$.
• Es gibt nun drei Augenöffnungen und eben so viele Schwellen.  Die Gleichung für die normierte Augenöffnung lautet nun:   $ö_{\rm norm} = g_0/3 -2 \cdot (|g_1| + |g_2| + \text{...}).$
• Der normierte Detektionsrauscheffektivwert  $\sigma_{\rm norm}$  ist beim Quaternärsystem wieder um den Faktor  $\sqrt{5/9} \approx 0.745$  kleiner als beim Binärsystem.

Pseudoternärcodes

Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol  $q_\nu$  ein Codesymbol  $c_\nu$  erzeugt, das außer vom aktuellen Eingangssymbol  $q_\nu$  auch von den  $N_{\rm C}$  vorangegangenen Symbolen  $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}}$  abhängt.  $N_{\rm C}$  bezeichnet man als die Ordnung  des Codes.  Typisch für eine symbolweise Codierung ist, dass

• die Symboldauer  $T$  des Codersignals (und des Sendesignals) mit der Bitdauer  $T_{\rm B}$  des binären Quellensignals übereinstimmt, und
• Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.
  
  

Blockschaltbild und Ersatzschaltbild eines Pseudoternärcoders

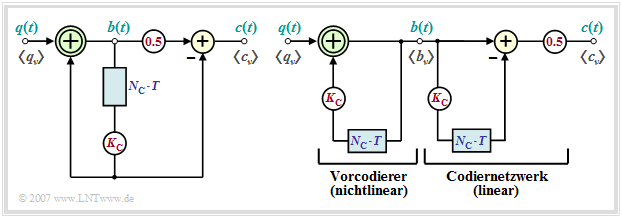
Besondere Bedeutung besitzen Pseudoternärcodes   ⇒   Stufenzahl  $M = 3$, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist. Genaueres hierzu finden Sie im  $\rm LNTwww$–Theorieteil.  Fazit:

• Umcodierung von binär  $(M_q = 2)$  auf ternär  $(M = M_c = 3)$:

$$q_\nu \in \{-1, +1\},\hspace{0.5cm} c_\nu \in \{-1, \ 0, +1\}\hspace{0.05cm}.$$

• Die relative Coderedundanz ist für alle Pseudoternärcodes gleich:

$$r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$

Anhand des Codeparameters  $K_{\rm C}$  werden verschiedene Pseudoternärcodes erster Ordnung  $(N_{\rm C} = 1)$  charakterisiert.

Signale bei der AMI-Codierung

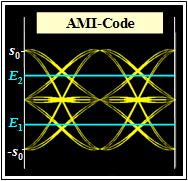
$\Rightarrow \ \ K_{\rm C} = 1\text{: AMI–Code}$  (von:   Alternate Mark Inversion)

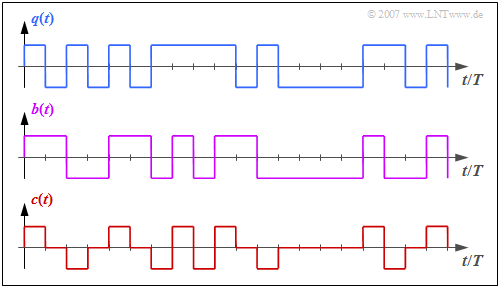
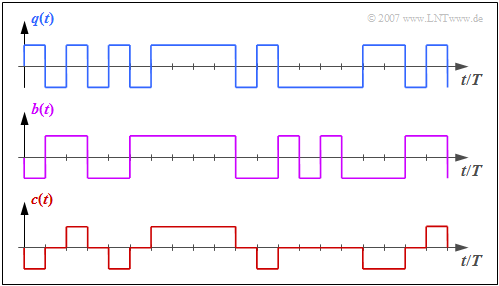
Die Grafik zeigt oben das binäre Quellensignal  $q(t)$. Darunter sind dargestellt:

• das ebenfalls binäre Signal  $b(t)$  nach dem Vorcodierer, und
• das Codersignal  $c(t) = s(t)$  des AMI–Codes.

Man erkennt das einfache AMI–Codierprinzip:

• Jeder Binärwert  „–1”  von $q(t)$   ⇒   Symbol  $\rm L$  wird durch den ternären Amplitudenkoeffizienten  $a_\nu = 0$  codiert.
  
• Der Binärwert  „+1”  von  $q(t)$   ⇒   Symbol  $\rm H$  wird alternierend mit  $a_\nu = +1$  und  $a_\nu = -1$  dargestellt.
  
  

Damit wird sichergestellt, dass im AMI–codierten Signal keine langen  „+1”–  bzw.  „–1”–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal problematisch wäre. 

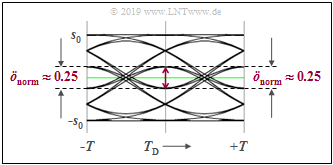
Links ist das Augendiagramm dargestellt.

•  Es gibt zwei Augenöffnungen und zwei Schwellen.
•  Die normierte Augenöffnung ist  $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1)$, wobei  $g_0 = g_d(t=0)$  den Hauptwert des Detektionsgrundimpulses bezeichnet und  $g_1 = g_d(t=\pm T)$  die relevanten Vor- und Nachläufer, die das Auge vertikal begrenzen.

•  Die normierte Augenöffnung ist somit deutlich kleiner als beim vergleichbaren Binäsystem   ⇒   $ö_{\rm norm}= g_0 -2 \cdot g_1$.
•  Der normierte Rauscheffektivwert  $\sigma_{\rm norm}$  ist um den Faktor  $\sqrt{1/2} \approx 0.707$  kleiner als beim vergleichbaren Binäsystem.

Signale bei der Duobinärcodierung

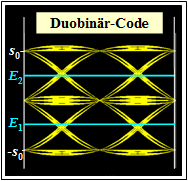
$\Rightarrow \ \ K_{\rm C} = -1\text{: Duobinärcode}$ 

Aus der rechten Grafik mit den Signalverläufen erkennt man:

• Hier können beliebig viele Symbole gleicher Polarität  („+1” bzw. „–1”)  direkt aufeinanderfolgen   ⇒   der Duobinärcode ist nicht gleichsignalfrei. 
• Dagegen tritt beim Duobinärcode die alternierende Folge  „ ... , +1, –1, +1, –1, +1, ... ”  nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist.
•  Auch die Duobinärcode–Folge besteht zu 50% aus Nullen. Der Verbesserungsfaktor durch das kleinere  $E_{\rm B}/ N_0$  ist wie beim AMI-Code gleich  $\sqrt{1/2} \approx 0.707$.

Links ist das Augendiagramm dargestellt.

•  Es gibt wieder zwei „Augen” und zwei Schwellen.
•  Die Augenöffnung ist   $ö_{\rm norm}= 1/2 \cdot (g_0 - g_1)$.

• $ö_{\rm norm}$  ist also größer als beim AMI–Code und auch wie beim vergleichbaren Binäsystem.
• Nachteilig gegenüber dem AMI–Code ist allerdings, dass er nicht gleichsignalfrei ist.

Exercises

• First select the number  $(1,\ 2, \text{...})$  of the exercise.  The number  $0$  corresponds to a "Reset":  Same setting as at program start.
• A task description is displayed.  The parameter values ​​are adjusted.  Solution after pressing "Show solution".
  

(1)  Explain the occurrence of the eye pattern for  $M=2 \text{, Gaussian low-pass, }f_{\rm G}/R_{\rm B} = 0.48$. For this, select "step–by–step".

•  The eye pattern is obtained by dividing the "useful" signal  $d_{\rm S}(t)$  (without noise) into pieces of duration  $2T$  and drawing these pieces on top of each other.
•  In  $d_{\rm S}(t)$  all  "five bit combinations"  must be contained   ⇒   at least  $2^5 = 32$  pieces   ⇒   at most  $32$  distinguishable lines.
•  The eye pattern evaluates the transient response of the signal.  The larger the (normalized) eye opening, the smaller are the intersymbol interferences.

(2)  Same setting as in  $(1)$. In addition,  $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$.  Evaluate the output characteristics  $ö_{\rm norm}$,  $\sigma_{\rm norm}$,  and  $p_{\rm U}$.

•  $ö_{\rm norm}= 0.542$  indicates that symbol detection is affected by adjacent pulses. For binary systems without intersymbol interference:  $ö_{\rm norm}= 1$.
•  The eye opening indicates only the signal  $d_{\rm S}(t)$  without noise.  The noise influence is captured by  $\sigma_{\rm norm}= 0.184$ . This value should be as small as possible.
•  The error probability  $p_{\rm U} = {\rm Q}(ö_{\rm norm}/\sigma_{\rm norm}\approx 0.16\%)$  refers solely to the "worst-case sequences", for Gaussian low–pass e.g.  $\text{...}\ , -1, -1, +1, -1, -1, \text{...}$.
•  Other sequences are less distorted   ⇒   the mean error probability  $p_{\rm M}$  is (usually) significantly smaller than $p_{\rm U}$  (describing the worst case).

(3)  The last settings remain.  With which  $f_{\rm G}/R_{\rm B}$  value does the worst case error probability  $p_{\rm U}$  become minimal?  Consider also the eye pattern.

•  The minimum value  $p_{\rm U, \ min} \approx 0.65 \cdot 10^{-4}$  is obtained for  $f_{\rm G}/R_{\rm B} \approx 0.8$, and this is almost independent of the setting of  $10 \cdot \lg \ E_{\rm B}/N_0$.
•  The normalized noise rms value does increase compared to the experiment  $(2)$  from  $\sigma_{\rm norm}= 0.168$  to  $\sigma_{\rm norm}= 0.238$.
•  However, this is more than compensated by the larger eye opening  $ö_{\rm norm}= 0.91$  compared to  $ö_{\rm norm}= 0.542$  $($magnification factor $\approx 1.68)$.

(4)  Which cutoff frequencies  $(f_{\rm G}/R_{\rm B})$  result in a completely inadequate error probability  $p_{\rm U} \approx 50\%$ ? Look at the eye pattern again  ("Overall view").

•  For  $f_{\rm G}/R_{\rm B}<0.28$  we get a "closed eye"  $(ö_{\rm norm}= 0)$  and thus a worst case error probability on the order of  $50\%$.
•  The decision on unfavorably framed bits must then be random, even with low noise  $(10 \cdot \lg \ E_{\rm B}/N_0 = 16 \ {\rm dB})$.

(5)  Now select the settings  $M=2 \text{, Matched Filter receiver, }T_{\rm E}/T = 1$,  $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$  and  "Overall view". Interpret the results.

•  The basic detection impulse  $g_d(t)$  is triangular and the eye is "fully open".  Consequently, the normalized eye opening is  $ö_{\rm norm}= 1.$
•  From  $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$  it follows $E_{\rm B}/N_0 = 10$   ⇒   $\sigma_{\rm norm} =\sqrt{1/(2\cdot E_{\rm B}/ N_0)} = \sqrt{0.05} \approx 0.224$  ⇒   $p_{\rm U} = {\rm Q}(4.47) \approx 3.9 \cdot 10^{-6}.$
•  This  $p_{\rm U}$ value is by a factor  $15$  better than in  $(3)$.   But:  For  $H_{\rm K}(f) \ne 1$  this so–called "Matched Filter Receiver" is not applicable.

(6)  Same settings as in  $(5)$.  Now vary  $T_{\rm E}/T$  in the range between  $0.5$  and  $1.5$.  Interpret the results.

•  For  $T_{\rm E}/T < 1$ ,  $ö_{\rm norm}= 1$  still holds.  But  $\sigma_{\rm norm}$  becomes larger, for example  $\sigma_{\rm norm} = 0.316$  for  $T_{\rm E}/T =0.5$   ⇒   the filter is too broadband!
•  $T_{\rm E}/T > 1$  results in a smaller  $\sigma_{\rm norm}$  compared to  $(5)$.  But the "eye" is no longer open, e.g.  $T_{\rm E}/T =1.25$:   $ö_{\rm norm}= g_0 - 2 \cdot g_1 = 0.6$.

(7)  Now select the settings  $M=2 \text{, CRO Nyquist system, }r_f = 0.2$  and  "Overall view". Interpret the eye pattern, also for other  $r_f$ values.

•  Unlike  $(6)$  here the basic detection impulse is not zero for  $|t|>T$,  but  $g_d(t)$  has equidistant zero crossings:  $g_0 = 1, \ g_1 = g_2 = 0$   ⇒   Nyquist system.
•  All  $32$  eye lines pass through only two points at  $t=0$.  The vertical eye opening is maximum for all  $r_f$    ⇒    $ö_{\rm norm}= 1$.
•  In contrast, the horizontal eye opening increases with  $r_f$  and is for  $r_f = 1$  maximum equal to  $T$   ⇒   the phase jitter has no influence in this case.

(8)  Same setting as in  $(7)$.  Now vary  $r_f$  with respect to minimum error probability.  Interpret the results.

• $ö_{\rm norm}= 1$  always holds.  In contrast,  $\sigma_{\rm norm}$  shows a slight dependence on  $r_f$.  The minimum  $\sigma_{\rm norm}=0.236$  results for  $r_f = 0.9$   ⇒   $p_{\rm U} \approx 1.1 \cdot 10^{-5}.$
•  Compared to the best possible case according to  $(5)$   ⇒   "Matched Filter Receiver"  $p_{\rm U}$  is three times larger, although  $\sigma_{\rm norm}$  is only larger by about  $5\%$.
•  The larger  $\sigma_{\rm norm}$ value is due to the exaggeration of the noise PDS to compensate for the drop through the transmitter frequency response  $H_{\rm S}(f)$.

(9)  Select the settings  $M=4 \text{, Matched Filter receiver, }T_{\rm E}/T = 1$,  $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$  and  $12 \ {\rm dB}$.  Interpret the results.

•  Now there are three eye openings.  Compared to  $(5)$   $ö_{\rm norm}$  is thus smaller by a factor of  $3$.  $\sigma_{\rm norm}$  on the other hand, only by a factor of  $\sqrt{5/9)} \approx 0.75$.
•  For  $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$  the  (worst–case)  error probability is  $p_{\rm U} \approx 2.27\%$  and for  $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$  approx.  $0.59\%$.

(10)  For the remaining tasks, always  $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Consider the eye pattern  ("overall view")  for  $M=4 \text{, CRO Nyquist system, }r_f = 0.5$.

•  In the analyzed  $d_{\rm S}(t)$  region all  "five symbol combinations"  must be contained   ⇒   minimum  $4^5 = 1024$  parts   ⇒   maximum  $1024$  distinguishable lines.
•  All  $1024$  eye lines pass through only four points at  $t=0$ :   $ö_{\rm norm}= 0.333$.  $\sigma_{\rm norm} = 0.143$  is slightly larger than in  $(9)$  ⇒   $p_{\rm U} \approx 1\%$.

(11)  Select the settings  $M=4 \text{, Gaussian low-pass, }f_{\rm G}/R_{\rm B} = 0.48$  and vary  $f_{\rm G}/R_{\rm B}$.  Interpret the results.

•  $f_{\rm G}/R_{\rm B}=0.48$  leads to the minimum error probability  $p_{\rm U} \approx 0.21\%$.  $\text{Compromise between}$  $ö_{\rm norm}= 0.312$  and  $\sigma_{\rm norm}= 0.109$.
•  If the cutoff frequency is too small, intersymbol interference dominates.  Example:  $f_{\rm G}/R_{\rm B}= 0.3$:  $ö_{\rm norm}= 0.157;$ $\sigma_{\rm norm}= 0.086$  ⇒    $p_{\rm U} \approx 3.5\%$.
•  If the cutoff frequency is too high, noise dominates.  Example:  $f_{\rm G}/R_{\rm B}= 1.0$:  $ö_{\rm norm}= 0.333;$ $\sigma_{\rm norm}= 0.157$  ⇒    $p_{\rm U} \approx 1.7\%$.
•  From the comparison with  $(9)$  one can see:  $\text{With quaternary coding it is more convenient to allow intersymbol interference}$.

(12)  What differences does the eye pattern show for  $M=3 \text{ (AMI code), Gaussian low-pass, }f_{\rm G}/R_{\rm B} = 0.48$  compared to the binary system  $(1)$? Interpretation.

•  The basic detection impulse  $g_d(t)$  is the same in both cases.  The sample values are respectively  $g_0 = 0.771, \ g_1 = 0.114$.
•  With the AMI code, there are two eye openings with each  $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1) = 0.214$.  With the binary code:  $ö_{\rm norm}= g_0 -2 \cdot g_1 = 0.543$.
•  The AMI sequence consists of  $50\%$  zeros.  The symbols  $+1$  and  $-1$  alternate   ⇒   there is no long  $+1$  sequence and no long  $-1$  sequence.
•  Therein lies the only advantage of the AMI code:  This can also be applied to a channel with  $H_{\rm K}(f= 0)=0$  ⇒   a DC signal is suppressed.

(13)  Same setting as in  $(12)$.  Select additionally  $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$.  Analyze the worst-case error probability of the AMI code.

•  Despite smaller  $\sigma_{\rm norm} = 0.103$  the AMI code has higher error probability  $p_{\rm U} \approx 2\%$  than the binary code:  $\sigma_{\rm norm} = 0.146, \ p_{\rm U} \approx \cdot 10^{-4}.$
•  $f_{\rm G}/R_{\rm B}<0.34$  results in a closed eye  $(ö_{\rm norm}= 0)$  ⇒    $p_{\rm U} =50\%$.  With binary coding:  For  $f_{\rm G}/R_{\rm B}>0.34$  the eye is open.

(14)  What differences does the eye pattern show for  $M=3 \text{ (Duobinary code), Gaussian low-pass, }f_{\rm G}/R_{\rm B} = 0.30$  compared to the binary system  (1)?

•  With redundancy-free binary code:  $ö_{\rm norm}= 0.096, \ \sigma_{\rm norm} = 0.116 \ p_{\rm U} \approx 20\%$.   With Duobinary code:  $ö_{\rm norm}= 0.167, \ \sigma_{\rm norm} = 0.082 \ p_{\rm U} \approx 2\%$.
• In particular, with small  $f_{\rm G}/R_{\rm B}$  the Duobinary code gives good results, since the transitions from  $+1$  to  $-1$  (and vice versa) are absent in the eye pattern.
• Even with  $f_{\rm G}/R_{\rm B}=0.2$  the eye is open.  But in contrast to AMI  the Duobinary code is not applicable with a DC-free channel   ⇒   $H_{\rm K}(f= 0)=0$.

Applet Manual

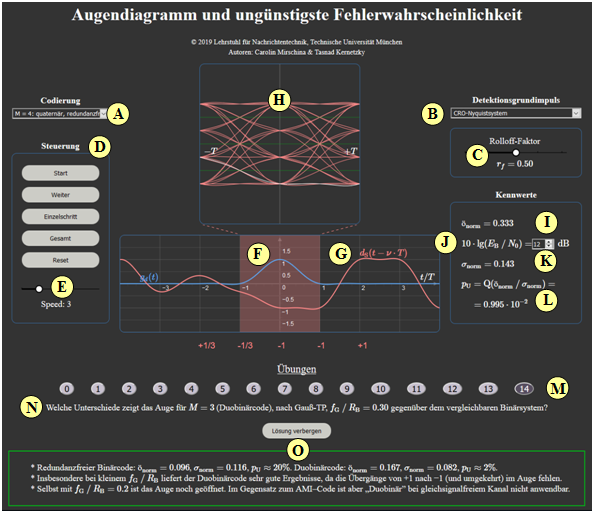
    (A)     Auswahl:   Codierung
                   (binär,  quaternär,  AMI–Code,  Duobinärcode)

    (B)     Auswahl:   Detektionsgrundimpuls
                    (nach Gauß–TP,  CRO–Nyquist,  nach Spalt–TP}

    (C)     Prametereingabe zu  (B)
                   (Grenzfrequenz,  Rolloff–Faktor,  Rechteckdauer)

    (D)     Steuerung der Augendiagrammdarstellung
                   (Start,  Pause/Weiter,  Einzelschritt,  Gesamt,  Reset)

    (E)     Geschwindigkeit der Augendiagrammdarstellung

    (F)     Darstellung:  Detektionsgrundimpuls  $g_d(t)$

    (G)     Darstellung:  Detektionsnutzsignal  $d_{\rm S}(t - \nu \cdot T)$

    (H)     Darstellung:  Augendiagramm im Bereich  $\pm T$

    ( I )     Numerikausgabe:  $ö_{\rm norm}$  (normierte Augenöffnung)

    (J)     Prametereingabe  $10 \cdot \lg \ E_{\rm B}/N_0$  für  (K)

    (K)     Numerikausgabe:  $\sigma_{\rm norm}$  (normierter Rauscheffektivwert)

    (L)     Numerikausgabe:  $p_{\rm U}$  (ungünstigste Fehlerwahrscheinlichkeit)

    (M)     Bereich für die Versuchsdurchführung:   Aufgabenauswahl

    (N)     Bereich für die Versuchsdurchführung:   Aufgabenstellung

    (O)     Bereich für die Versuchsdurchführung:   Musterlösung einblenden

About the Authors

This interactive calculation tool was designed and implemented at the  Institute for Communications Engineering  at the  Technical University of Munich.

• The first version was created in 2008 by Thomas Großer  as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).

• Last revision and English version 2020/2021 by  Carolin Mirschina  in the context of a working student activity.  Translation using DEEPL.com.

The conversion of this applet to HTML 5 was financially supported by  Studienzuschüsse  ("study grants")  of the TUM Faculty EI.  We thank.

Once again: Open Applet in new Tab

Open Applet in a new tab       German Version