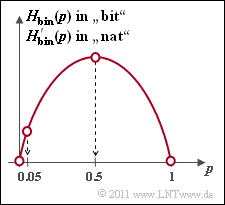
Exercise 1.1Z: Binary Entropy Function
We consider a sequence of binary random variables with the symbol set $\{ \rm A, \ B \}$ ⇒ $M = 2$. Let the probabilities of occurrence of the two symbols be $p_{\rm A }= p$ and $p_{\rm B } = 1 - p$.
The individual sequence elements are statistically independent. The entropy of this message source is equally valid:
- $$H_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ld}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ld}\hspace{0.1cm}\frac{1}{1-p}\hspace{0.15cm}{\rm in \hspace{0.15cm} \big [bit \big ]}\hspace{0.05cm},$$
- $$ H'_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ln}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ln}\hspace{0.1cm}\frac{1}{1-p}\hspace{0.15cm}{\rm in \hspace{0.15cm} \big [nat\big ]}\hspace{0.05cm}.$$
In these equations, the shorthand terms used are:
- the natural logarithm ⇒ $ {\ln} \hspace{0.09cm} p = \log_{\rm e} \hspace{0.05cm} p$,
- the binary logarithm ⇒ ${\rm ld} \hspace{0.09cm} p = \log_2 \hspace{0.05cm} p$.
The plot shows the binary entropy function as a function of the parameter $p$, assuming $0 ≤ p ≤ 1$ .
In subtasks (5) and (6) the relative error is to be determined if the symbol probability $p$ was determined by simulation $($i.e., as a relative frequency $h)$ , resulting in $h = 0.9 \cdot p$ by mistake. The relative error is then given as follows:
- $$\varepsilon_{H} = \frac{H_{\rm bin}(h)- H_{\rm bin}(p)}{H_{\rm bin}(p)}\hspace{0.05cm}.$$
Hint:
- The task belongs to the chapter Discrete Memoryless Sources.
Questions
Solution
- The entropy function $H'_{\rm bin}(p)$ is according to the specification:
- $$H'_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ln}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ln}\hspace{0.1cm}\frac{1}{1-p} = {\rm ln}\hspace{0.1cm}2 \cdot \left [ p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p}\right ]$$
- $$\Rightarrow \hspace{0.3cm} H'_{\rm bin}(p) \hspace{0.15cm}{\rm (in \hspace{0.15cm} nat)}= {\rm ln}\hspace{0.1cm}2 \cdot H_{\rm bin}(p) \hspace{0.15cm}{\rm (in \hspace{0.15cm} bit)} = 0.693\cdot H_{\rm bin}(p)\hspace{0.05cm}.$$
(2) The optimisation condition is ${\rm d}H_{\rm bin}(p)/{\rm d}p = 0$ resp.
- $$\frac{{\rm d}H'_{\rm bin}(p)}{{\rm d}p} \stackrel{!}{=} 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{\rm d}{{\rm d}p} \big [ - p \cdot {\rm ln}\hspace{0.1cm}p - (1-p) \cdot {\rm ln}\hspace{0.1cm}({1-p})\big ] \stackrel{!}{=} 0$$
- $$\Rightarrow \hspace{0.3cm} - {\rm ln}\hspace{0.1cm}p - p \cdot \frac {1}{p}+ {\rm ln}\hspace{0.1cm}(1-p) + (1-p)\cdot \frac {1}{1- p}\stackrel{!}{=} 0$$
- $$\Rightarrow \hspace{0.3cm} {\rm ln}\hspace{0.1cm}\frac {1-p}{p}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac {1-p}{p}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline { p = 0.5}\hspace{0.05cm}.$$
- Die Entropiewerte für $p = 0.5$ lauten somit:
- $$H'_{\rm bin}(p = 0.5) \hspace{0.1cm} = \hspace{0.1cm} -2 \cdot 0.5 \cdot {\rm ln}\hspace{0.1cm}0.5 = {\rm ln}\hspace{0.1cm}2 = 0.693 \, {\rm nat}\hspace{0.05cm},$$
- $$ H_{\rm bin}(p = 0.5) \hspace{0.1cm} = \hspace{0.1cm} -2 \cdot 0.5 \cdot {\rm ld}\hspace{0.1cm}0.5 = {\rm log_2}\hspace{0.1cm}2 \hspace{0.15cm}\underline {= 1 \, {\rm bit}}\hspace{0.05cm}.$$
(3) For $p = 5\%$ we get:
- $$H_{\rm bin}(p = 0.05) \hspace{0.1cm} = \hspace{0.1cm} 0.05 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.05}+ 0.95 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.95}= \frac{1}{0.693} \cdot \big [ 0.05 \cdot {\rm ln}\hspace{0.1cm}20+ 0.95 \cdot {\rm ln}\hspace{0.1cm}1.053\big ] \hspace{0.15cm}\underline {\approx 0.286 \, {\rm bit}}\hspace{0.05cm}.$$
(4) This sub-task cannot be solved in closed form, but by „trial and error”.
- A solution gives the result:
- $$H_{\rm bin}(p = 0.10) = 0.469 \, {\rm bit}\hspace{0.05cm},\hspace{0.2cm}H_{\rm bin}(p = 0.12) = 0.529 \, {\rm bit}\hspace{0.05cm},\hspace{0.2cm} H_{\rm bin}(p = 0.11) \approx 0.5 \, {\rm bit} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_1 \approx 0.11\hspace{0.05cm}. $$
- The second solution results from the symmetry of $H_{\rm bin}(p)$ zu $p_2 = 1 -p_1 \hspace{0.15cm}\underline{= 0.89}$.
(5) With $p = 0.45$ one obtains $H_{\rm bin}(p) = 0.993\hspace{0.05cm}\rm bit$. The relative error with respect to entropy is thus
- $$\varepsilon_{H} = \frac{H_{\rm bin}(p = 0.45)- H_{\rm bin}(p= 0.5)}{H_{\rm bin}(p = 0.5)}= \frac{0.993- 1}{1}\hspace{0.15cm}\underline {= -0.7 \, {\rm \%}} \hspace{0.05cm}.$$
- The minus sign indicates that the entropy value $H_{\rm bin}(p) = 0.993\hspace{0.05cm}\rm bit$ is too small.
- If the simulation had yielded the too large value $p = 0.55$ , the entropy and also the relative error would be just as large.
(6) $H_{\rm bin}(p = 0.045) = 0.265\hspace{0.05cm}\rm bit$ is valid..
- With the result of subtask (3) ⇒ $H_{\rm bin}(p = 0.05) = 0.286\hspace{0.05cm}\rm bit$ it follows for the relative error with respect to the entropy:
- $$\varepsilon_{H} = \frac{H_{\rm bin}(p = 0.045)- H_{\rm bin}(p= 0.05)}{H_{\rm bin}(p = 0.05)}= \frac{0.265- 0.286}{0.286}\hspace{0.15cm}\underline {= -7.3 \, {\rm \%}} \hspace{0.05cm}.$$
- The result shows:
- An incorrect determination of the symbol probabilities by $10\%$ is much more noticeable for $p = 0.05$ due to the steeper $H_{\rm bin}(p)$–Verlaufs deutlich stärker bemerkbar als für $p = 0.5$.
- A too large probability $p = 0.055$ would have led to $H_{\rm bin}(p = 0.055) = 0.307\hspace{0.05cm}\rm bit$ and thus to a distortion of $\varepsilon_H = +7.3\%$. In this range, the entropy curve is thus linear (with a good approximation).