Exercise 5.1Z: Sampling of Harmonic Oscillations
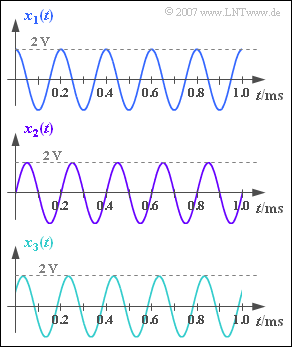
We consider three harmonic oscillations with the same frequency and the same amplitude:
- $$x_1(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_2(t) = A \cdot \sin (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_3(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - 60^{\circ}) \hspace{0.05cm}.$$
The oscillation parameters $f_0$ and $A$ can be taken from the graph.
It is assumed that the signals are sampled equidistantly at times $\nu \cdot T_{\rm A}$ whereby the parameter values $T_{\rm A} = 80 \ µ \text{s}$ and $T_{\rm A} = 100 \ µ \text{s}$ are to be analysed.
The signal reconstruction at the receiver takes place through a low-pass filter $H(f)$, which forms the signal $y_{\rm A}(t) = x_{\rm A}(t)$ from the sampled signal $y(t)$ . It applies:
- $$H(f) = \left\{ \begin{array}{c} 1 \\ 0.5 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_{\rm G} \hspace{0.05cm}, \\ |f| = f_{\rm G} \hspace{0.05cm}, \\ |f| > f_{\rm G} \hspace{0.05cm}, \\ \end{array}$$
Here $f_{\rm G}$ indicates the cut-off frequency of the rectangular low-pass filter. For this shall apply:
- $$f_{\rm G} = \frac{1}{ 2 \cdot T_{\rm A}}\hspace{0.05cm}.$$
The sampling theorem is fulfilled if $y(t) = x(t)$ holds.
Hints:
- This task belongs to the chapter Time-Discrete Signal Representation.
- There is an interactive applet for the topic dealt with here: Sampling of Analog Signals and Signal Reconstruction
Questions
Solution
- This results in the signal frequency $f_0 = 1/T_0 \; \underline{= 5 \ \text{kHz}}$.
(2) All proposed solutions are correct:
- The sampling rate here is $f_{\rm A} = 1/T_{\rm A} = 12.5 \ \text{kHz}$.
- This value is greater than $2 \cdot f_0 = 10 \ \text{kHz}$.
- Thus the sampling theorem is fulfilled independently of the phase and $y(t) = x(t)$ always applies.
(3) The sampling rate is now $f_{\rm A} = 2 \cdot f_0 = 10 \ \text{kHz}$.
- Only in the special case of the cosine signal is the sampling theorem now satisfied and it holds:
- $$y_1(t) = x_1(t) ⇒ A_1 \; \underline{=2 \ \text{V}} \text{ und }\varphi_1 \; \underline{= 0}.$$
This result is now to be derived mathematically, whereby a phase $\varphi$ in the input signal is already taken into account with regard to the remaining subtasks:
- $$x(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - \varphi) \hspace{0.05cm}.$$
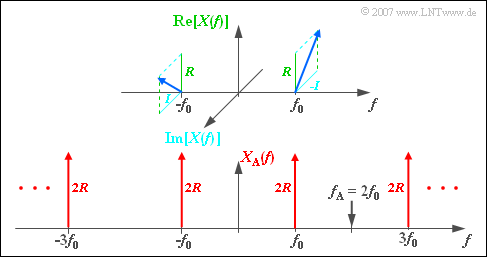
- Then, for the spectral function sketched in the graph above:
- $$X(f) = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f+ f_{\rm 0} ) + {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
- With the abbreviations
- $$R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi) \hspace{0.5cm}{\rm und} \hspace{0.5cm}I ={A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin(\varphi)$$
- can also be written for this:
- $$X(f) = (R + {\rm j} \cdot I) \cdot \delta (f+ f_{\rm 0} ) + (R - {\rm j} \cdot I) \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
- The spectrum of the signal $f_{\rm A} = 2f_0$ sampled with $x_{\rm A}(t)$ is thus:
- $$X_{\rm A}(f) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A}
)= \sum_{\mu = - \infty }^{+\infty} X (f- 2\mu \cdot f_{\rm 0}
)\hspace{0.05cm}.$$
- The bottom graph shows that $X_{\rm A}(f)$ consists of Dirac functions at $\pm f_0$, $\pm 3f_0$, $\pm 5f_0$, , and so on.
- All weights are purely real and equal to $2 \cdot R$.
- The imaginary parts of the periodically continued spectrum cancel out.
- If one further takes into account the rectangular low-pass filter whose cut-off frequency lies exactly at $f_{\rm G} = f_0$ , as well as $H(f_{\rm G}) = 0.5$, one obtains for the spectrum after signal reconstruction:
- $$Y(f) = R \cdot \delta (f+ f_{\rm 0} ) + R \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}, \hspace{0.5cm} R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi)\hspace{0.05cm}.$$
- The Fourier inverse transformation leads to
- $$y(t) = A \cdot \cos (\varphi)\cdot \cos (2 \pi \cdot f_0 \cdot t ) \hspace{0.05cm}.$$
- Thus, a cosine-shaped progression results independent of the input phase $\varphi$ .
- If $\varphi = 0$ as with the signal $x_1(t)$, the amplitude of the output signal is also equal to $A$.
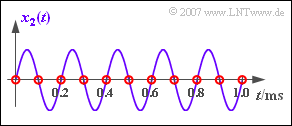
(4) The sine signal has the phase $90^\circ$.
- From this follows directly $y_2(t) = 0$ ⇒ amplitude $\underline{A_2 = 0}$.
- This result becomes understandable if you look at the samples in the graph.
- All samples (red circles) are zero, so there can be no signal even after the filter.
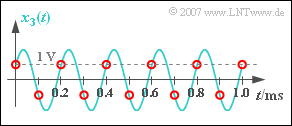
(5) Despite $\varphi = 60^\circ$ gilt $\varphi_3 = 0$ ⇒ the reconstructed signal $y_3(t)$ ist cosinusförmig. is also cosine-shaped. The amplitude is equal to
- $$A_3 = A \cdot \cos (60^{\circ})= {A}/{2} \hspace{0.15 cm}\underline{= 1\,{\rm V}} \hspace{0.05cm}.$$
- If you look at the samples drawn in red in the graph, you will admit that as a "signal reconstructor" you would not make any other decision than the low-pass.
- After all, you do not know the turquoise curve.