Exercise 4.10: Binary and Quaternary

Binärsignal $b(t)$ und Quaternärsignal $q(t)$

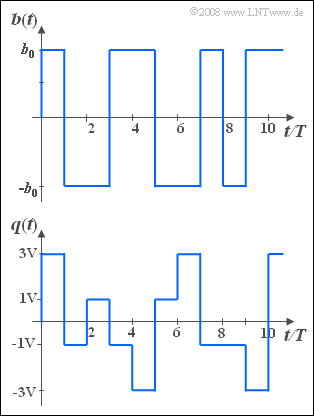
Wir betrachten hier ein Binärsignal $b(t)$ und ein Quarternärsignal $q(t)$, wobei gilt:

Die beiden Signale sind rechteckförmig, und die Dauer der einzelnen Rechtecke beträgt jeweils $T$ (Symboldauer).
Die durch die Impulshöhen der einzelnen Rechteckimpulse dargestellten Symbole $($mit Stufenzahl $M = 2$ bzw. $M = 4)$ sind statistisch unabhängig.
Wegen der bipolaren Signalkonstellation sind beide Signale gleichsignalfrei, wenn die Symbolwahrscheinlichkeiten geeignet (symmetrisch) gewählt werden.
Aufgrund der letztgenannten Eigenschaft folgt für die Wahrscheinlichkeiten der Binärsymbole:

$${\rm Pr}\big[b(t) = +b_0\big] = {\rm Pr}\big[b(t) = -b_0\big] ={1}/{2}.$$

Dagegen gelte für das Quarternärsignal:

$${\rm Pr}\big[q(t) = +3 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -3 \hspace{0.05cm}{\rm V}\big]= {1}/{6},$$

$${\rm Pr}\big[q(t) = +1 \hspace{0.05cm}{\rm V}\big] = {\rm Pr}\big[q(t) = -1 \hspace{0.05cm}{\rm V}\big]= {2}/{6}.$$

Hinweis:

Die Aufgabe gehört zum Kapitel Autokorrelationsfunktion.

Fragebogen

$\varphi_q(\tau = 0) \ = \ $

$\ \rm V^2$

$\varphi_q(\tau = T) \ = \ $

$\ \rm V^2$

$b_0\ = \ $

$\ \rm V$

Musterlösung

Solution

(1) Der AKF-Wert an der Stelle $\tau = 0$ entspricht der mittleren Signalleistung, also dem quadratischen Mittelwert von $q(t)$. Für diesen gilt:

Dreieckförmige AKF

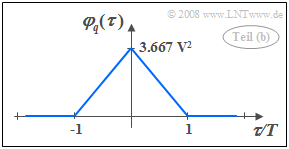
$$\varphi_q(\tau = 0)= {1}/{6 } \cdot ({\rm 3\,V})^2 + {2}/{6 } \cdot ({\rm 1\,V})^2 + {2}/{6 } \cdot (-{\rm 1\,V})^2 + {1}/{6 } \cdot (-{\rm 3\,V})^2= \rm {22}/{6 }\, \rm V^2\hspace{0.15cm}\underline{= \rm 3.667 \,V^2}.$$

(2) Die einzelnen Symbole wurden als statistisch unabhängig vorausgesetzt.

Deshalb und wegen des fehlenden Gleichanteils gilt hier für jeden ganzzahligen Wert von $\nu$:

$${\rm E} \big [ q(t) \cdot q ( t + \nu T) \big ] = {\rm E} \big [ q(t) \big ] \cdot {\rm E} \big [ q ( t + \nu T) \big ]\hspace{0.15cm}\underline{ = 0}.$$

Somit hat die gesuchte AKF den rechts skizzierten Verlauf.
Im Bereich $-T \le \tau \le +T$ ist die AKF aufgrund der rechteckförmigen Impulsform abschnittsweise linear, also dreieckförmig.

(3) Die AKF $\varphi_b(\tau)$ des Binärsignals ist aufgrund der statistisch unabhängigen Symbole im Bereich $| \tau| > T$ ebenfalls identisch Null, und für $-T \le \tau \le +T$ ergibt sich ebenfalls eine Dreiecksform.

Für den quadratischen Mittelwert erhält man:

$$\varphi_b (\tau = 0) = b_{\rm 0}^{\rm 2}.$$

Mit $b_0\hspace{0.15cm}\underline{= 1.915\, \rm V}$ sind die beiden Autokorrelationsfunktionen $\varphi_q(\tau)$ und $\varphi_b(\tau)$ identisch.

(4) Richtig sind die Lösungsvorschläge 1, 3 und 4.

Aus der Autokorrelationsfunktion lassen sich tatsächlich ermitteln:

die Periodendauer $T_0$: diese ist für die Mustersignale und die AKF gleich;
der lineare Mittelwert: Wurzel aus dem Endwert der AKF für $\tau \to \infty$ und
die Varianz: Differenz der AKF-Werte von $\tau = 0$ und $\tau \to \infty$.

Nicht ermittelt werden können:

die Wahrscheinlichkeitsdichtefunktion: trotz $\varphi_q(\tau) =\varphi_b(\tau)$ ist $f_q(q) \ne f_b(b)$;
die Momente höherer Ordnung: für deren Berechnung benötigt man die WDF;
Alle Phasenbeziehungen und Symmetrieeigenschaften sind aus der AKF nicht erkennbar.

	Periodendauer.
	Wahrscheinlichkeitsdichtefunktion.
	Linearer Mittelwert.
	Varianz.
	Moment 3. Ordnung.
	Phasenbeziehungen.