Exercise 4.3: Algebraic and Modulo Sum

Algebraic & modulo–2 sum

Table for moment calculation

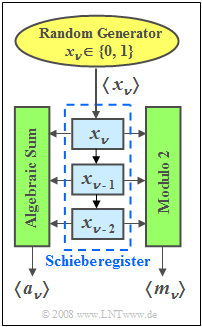
A "clocked" random number generator returns a sequence $\langle x_\nu \rangle$ of binary random numbers.

It is assumed that the binary numbers $0$ and $1$ occur with equal probabilities and that the individual random numbers do not depend on each other.
The random numbers $ x_\nu \in \{0, 1\}$ are entered into the first memory location of a shift register and shifted down one digit with each clock pulse.

Two new random sequences $\langle a_\nu \rangle$ and $\langle m_\nu \rangle$ are formed from the contents of the three-digit shift register. Here denotes:

the "algebraic sum" $a_\nu$:

$$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$

the "modulo–2 sum" $m_\nu$:

$$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$

Hints:

This exercise belongs to the chapter Two-Dimensional Random Variables.
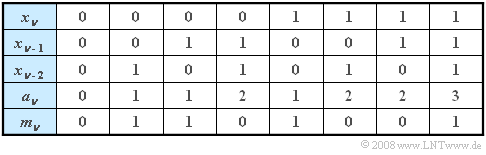
Use the following table for moment calculation.

Questions

Solution

(1) It can be seen from the table on the information page that for the modulo–2 sum, the two values $0$ and $1$ have equal probability:

$${\rm Pr}(m_\nu = 0) = {\rm Pr}(m_\nu = 1)\hspace{0.15cm}\underline{=0.5}.$$

(2) The table shows that for each preassignment ⇒ $( x_{\nu-1}, x_{\nu-2}) = (0,0), (0,1), (1,0), (1,1)$ the values $m_\nu = 0$ and $m_\nu = 1$ resp. are equally likely.

Expressed differently: ${\rm Pr}(m_{\nu}\hspace{0.05cm}|\hspace{0.05cm}m_{\nu-1}) = {\rm Pr}( m_{\nu}).$
This exactly matches the definition of "statistical independence" ⇒ Answer 1.

2D PDF of $x$ and $m$

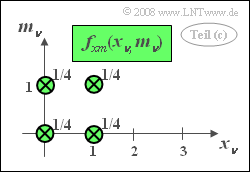
(3) Correct are the second and the last suggested solutions.

The 2D PDF consists of four Dirac functions, each with weight $1/4$.
One obtains this result, for example, by evaluating the table on the data page.
Since $f_{xm}(x_\nu, m_\nu)$ is equal to the product $f_{x}(x_\nu) \cdot f_{m}(m_\nu)$ the quantities $x_\nu$ and $m_\nu$ are statistically independent.
Statistically independent random variables, however, are also linearly statistically independent, so they are certainly uncorrelated.

(4) Within the sequence $\langle a_\nu \rangle$ of algebraic sum there are statistical bindings ⇒ Answer 2.

You can see this because the unconditional probability $ {\rm Pr}( a_{\nu} = 0) =1/8$ is,
while, for example ${\rm Pr}(a_{\nu} = 0\hspace{0.05cm}|\hspace{0.05cm}a_{\nu-1} = 3) =0$ holds.

2D PDF of $a$ and $m$

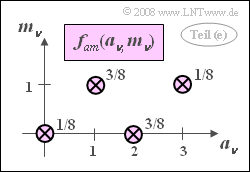
(5) Correct are the first and the last suggested solutions:

As in the subtask (3) there are again four Dirac functions, but this time not with equal momentum weights $1/4$.
The two-dimensional PDF thus cannot be written as a product of the two marginal probability densities.
But this means that statistical bindings must exist between $a_\nu$ and $m_\nu$ .
For the joint expected value, one obtains:

$${\rm E}\big[a\cdot m \big] = \rm \frac{1}{8}\cdot 0 \cdot 0 +\frac{3}{8}\cdot 2 \cdot 0 +\frac{3}{8}\cdot 1 \cdot 1 + \frac{1}{8}\cdot 3 \cdot 1 = \frac{3}{4}.$$

With the linear means ${\rm E}\big[a \big] = 1.5$ and ${\rm E}[m] = 0.5$ it thus follows for the covariance:

$$\mu_{am}= {\rm E}\big[ a\cdot m \big] - {\rm E}\big[ a \big]\cdot {\rm E} \big[ m \big] = \rm 0.75-1.5\cdot 0.5 = \rm 0.$$

Thus, the correlation coefficient $\rho_{am}= 0$. That is, The dependencies present are nonlinear.
The quantities $a_\nu$ and $m_\nu$ are statistically dependent, but still uncorrelated.

	The random variables $x_\nu$ and $m_\nu$ are statistically dependent.
	The random variables $x_\nu$ and $m_\nu$ are statistically independent.
	The random variables $x_\nu$ and $m_\nu$ are correlated.
	The random variables $x_\nu$ and $m_\nu$ are uncorrelated.

	The random variables $a_\nu$ and $m_\nu$ are statistically dependent.
	The random variables $a_\nu$ and $m_\nu$ are statistically independent.
	The random variables $a_\nu$ and $m_\nu$ are correlated.
	The random variables $a_\nu$ and $m_\nu$ are uncorrelated.

	The sequence elements $m_\nu$ are statistically independent.
	There are statistical bindings within the sequence $\langle m_\nu \rangle$.

	The sequence elements $a_\nu$ are statistically independent.
	There are statistical bindings within the sequence $\langle a_\nu \rangle$.