Exercise 2.6Z: Signal-to-Noise Ratio
In the following exercise, we assume:
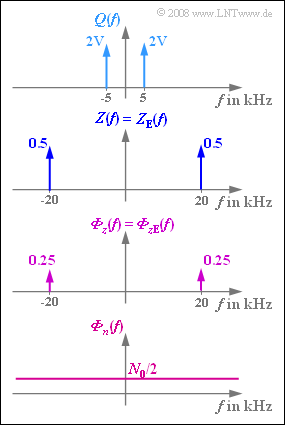
- a cosine source signal:
- $$ q(t) = 4 \,{\rm V} \cdot \cos(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm},$$
- DSB–AM by multiplication with
- $$z(t) = 1 \cdot \cos(2 \pi \cdot 20\,{\rm kHz} \cdot t )\hspace{0.05cm},$$
- a frequency-independent attenuation on the channel corresponding to $α_{\rm K} = 10^{–4}$,
- additive white input noise with power density $N_0 = 4 · 10^{–19} \ \rm W/Hz$,
- phase-synchronous and frequency-synchronous demodulation by multiplication the same $z(t)$ as at the transmitter,
- a rectangular low-pass at the synchronous demodulator with cutoff frequency $f_{\rm E} = 5 \ \rm kHz$.
In the graph, these specifications are shown in the spectral domain. It should be explicitly mentioned that the power spectral density ${\it Φ}_z(f)$ of the cosine oscillation $z(t)$ is composed of two Dirac lines at $±f_{\rm T}$, as in the amplitude spectrum $Z(f)$, but with weight $A^2/4$ instead of $A/2$. The amplitude should always be set to $A=1$ in this exercise.
The sink signal $v(t)$ is composed of the useful component $α · q(t)$ and the noise component $ε(t)$ . Thus, the general rule for the signal-to-noise power ratio to be determined is:
- $$ \rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon}\hspace{0.05cm}.$$
This important quality criterion is often abbreviated to $\rm SNR$ ("signal–to–noise power ratio").
Hints:
- This exercise belongs to the chapter Synchronous Demodulation.
- Particular reference is made to the pages Calculating noise power and Relationship between the powers from source and_transmitted signal.
- Please note that the variables $α$ and $α_{\rm K}$ need not be the same.
- All powers refer to a resistance of $R = 50 \ \rm Ω$ with the exception of subtask (1).
- For DSB-AM without carrier, $P_q$ also represents the transmit power $P_{\rm S}$.
Questions
Solution
- The power is obtained from the integral over the PDS and is thus equal to the sum of the two Dirac weights.
- Thus, when $A = 4 \ \rm V$, we obtain the power of the source signal:
- $$ P_q = \frac{A^2}{2} \hspace{0.15cm}\underline {= 8\,{\rm V^2}} \hspace{0.05cm}.$$
- For the modulation method "DSB-AM without a carrier", this is also the transmit power $P_{\rm S}$ in reference to the unit resistance $1\ \rm Ω$.
(2) According to the elementary laws of Electrical Engineering:
- $$P_q = \frac{8\,{\rm V^2}}{50\,{\Omega}} \hspace{0.15cm}\underline {= 0.16\,{\rm W}} \hspace{0.05cm}.$$
(3) In the theory section, it is shown that $v(t) = q(t)$ holds under ideal conditions. However, the following should be taken into account:
- From the graph, it can be seen that $Z_{\rm E}(f) = Z(f)$ holds. Thus, the receiver-side carrier signal $z_{\rm E}(t)$ has like $z(t)$ the amplitude $1$.
- Ideally, however, the receiver-side carrier signal $z_{\rm E}(t)$ should have amplitude $2$.
- Therefore, $υ(t) = q(t)/2$ applies here.
- If we further consider the channel attenuation $α_{\rm K} = 10^{–4}$, we obtain the final result: $α\hspace{0.15cm}\underline { = 0.5 · 10^{–4}}.$
(4) The power spectral density of the product $n(t) · z(t)$ is obtained by convolving the two power density spectra of $n(t)$ and $z(t)$:
- $$ {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) = {\it \Phi}_n (f) \star {\it \Phi}_{z }(f)= \frac{N_0}{2} \star \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]= N_0 \hspace{0.05cm}.$$
- For the power spectral density of the signal $ε(t)$ after the low-pass filter, we obtain a rectangular shape with the same value at $f = 0$:
- $${\it \Phi}_\varepsilon (f) = {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) \cdot |H_{\rm E}(f)|^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\it \Phi}_\varepsilon (f=0)= N_0\hspace{0.15cm}\underline {= 4 \cdot 10^{-19}\,{\rm W/Hz}} \hspace{0.05cm}.$$
(5) The noise power is the integral over the noise power density:
- $$ P_{\varepsilon} = \int_{-f_{\rm E}}^{ + f_{\rm E}} {{\it \Phi}_\varepsilon (f)}\hspace{0.1cm}{\rm d}f = N_0 \cdot 2 f_{\rm E} = 4 \cdot 10^{-19}\,\frac{ \rm W}{\rm Hz} \cdot 10^{4}\,{\rm Hz} \hspace{0.15cm}\underline {= 4 \cdot 10^{-15}\,{\rm W}}\hspace{0.05cm}.$$
(6) From the results of subtasks (2), (3) and (5) it follows that:
- $$\rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon} = \frac{(0.5 \cdot 10^{-4})^2 \cdot 0.16\,{\rm W}}{4 \cdot 10^{-15}\,{\rm W}} \hspace{0.15cm}\underline {= 100000} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg }\hspace{0.1cm}\rho_{v } \hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$