Contents
Wiener-Khintchine Theorem
In the remainder of this paper we restrict ourselves to ergodic processes. As was shown in last chapter the following statements then hold:
- Each individual sample function $x_i(t)$ is representative of the entire random process $\{x_i(t)\}$.
- All time means are thus identical to the corresponding coulter means.
- The autocorrelation function, which is generally affected by the two time parameters $t_1$ and $t_2$ now depends only on the time difference $τ = t_2 - t_1$ :
- $$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$
The autocorrelation function provides quantitative information about the (linear) statistical bindings within the ergodic process $\{x_i(t)\}$ in the time domain. The equivalent descriptor in the frequency domain is the power spectral density , often referred to as the power density spectrum.
$\text{Definition:}$ The power spectral density (PSD) of an ergodic random process $\{x_i(t)\}$ is the Fourier transform of the auto-correlation function (ACF):
- $${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} \tau. $$
This functional is called the theorem of Wiener and Khinchin.
Similarly, the ACF can be computed as the inverse Fourier transform of the PSD (see page inverse Fourier transform in the book "Signal Representation"):
- $$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} f.$$
- The two equations are directly applicable only if the random process contains neither a DC component nor periodic components.
- Otherwise, one must proceed according to the specifications given in page Power spectral density with DC component .
Physical interpretation and measurement
Das folgende Bild zeigt eine Anordnung zur (näherungsweisen) messtechnischen Bestimmung des Leistungsdichtespektrums ${\it \Phi}_x(f)$.
Hierzu ist Folgendes anzumerken:
- Das Zufallssignal $x(t)$ wird auf ein (möglichst) rechteckförmiges und (möglichst) schmalbandiges Filter mit Mittenfrequenz $f$ und Bandbreite $Δf$ gegeben, wobei $Δf$ entsprechend der gewünschten Frequenzauflösung hinreichend klein gewählt werden muss.
- Das entsprechende Ausgangssignal $x_f(t)$ wird quadriert und anschließend der Mittelwert über eine hinreichend lange Messdauer $T_{\rm M}$ gebildet. Damit erhält man die Leistung von $x_f(t)$ bzw. die Leistungsanteile von $x(t)$ im Spektralbereich von $f - Δf/2$ bis $f + Δf/2$:
- $$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm}\rm d \it t.$$
- Die Division durch $Δf$ führt von der spektralen Leistung zur spektralen Leistungsdichte:
- $${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} {\rm bzw.} \hspace {0.5cm} {\it \Phi}_{x}(f) = \frac{P_{x_f}}{{\rm 2 \cdot \Delta} f}.$$
- Hierbei bezeichnet ${\it \Phi}_{x+}(f) = 2 · {\it \Phi}_x(f)$ das einseitige, nur für positive Frequenzen definierte LDS. Für negative Frequenzen ist ${\it \Phi}_{x+}(f) = 0$. Im Gegensatz dazu gilt für das üblicherweise verwendete zweiseitige LDS: ${\it \Phi}_x(–f) = {\it \Phi}_x(f)$.
- Während die Leistung $P_{x_f}$ mit kleiner werdender Bandbreite $Δf$ gegen Null tendiert, bleibt die spektrale Leistungsdichte ab einem hinreichend kleinen Wert von $Δf$ nahezu konstant. Für die exakte Bestimmung von ${\it \Phi}_x(f)$ sind zwei Grenzübergänge notwendig:
- $${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$
$\text{Fazit:}$
- Aus dieser physikalischen Interpretation folgt weiter, dass das Leistungsdichtespektrum stets reell ist und nie negativ werden kann.
- Die gesamte Signalleistung von $x(t)$ erhält man dann durch Integration über alle Spektralanteile:
- $$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$
Reziprozitätsgesetz von AKF-Zeitdauer und LDS-Bandbreite
Alle im Buch „Signaldarstellung” für deterministische Signale hergeleiteten Gesetzmäßigkeiten der Fouriertransformation können auch auf die Autokorrelationsfunktion (AKF) und das Leistungsdichtespektrum (LDS) eines Zufallsprozesses angewendet werden.
Aufgrund der spezifischen Eigenschaften
- von Autokorrelationsfunktion (stets reell und gerade)
- und Leistungsdichtespektrum (stets reell, gerade und nicht–negativ)
liefern allerdings nicht alle Gesetze sinnvolle Ergebnisse.
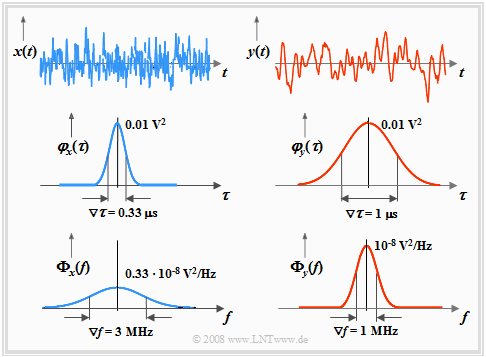
Wir betrachten nun wie im Abschnitt Interpretation der Autokorrelationsfunktion zwei unterschiedliche ergodische Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ anhand
- der beiden Mustersignale $x(t)$ und $y(t)$ ⇒ obere Skizze,
- der beiden Autokorrelationsfunktionen $φ_x(τ)$ und $φ_y(τ)$ ⇒ mittlere Skizze,
- der beiden Leistungsdichtespektren ${\it \Phi}_x(f)$ und ${\it \Phi}_y(f)$ ⇒ untere Skizze.
Anhand dieser Grafiken sind folgende Aussagen möglich:
- Die Flächen unter den LDS-Kurven sind gleich ⇒ die Prozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ besitzen gleiche Leistung:
- $${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$
- Das aus der klassischen (deterministischen) Systemtheorie bekannte Reziprozitätsgesetz von Zeitdauer und Bandbreite gilt hier ebenfalls:
Eine schmale Autokorrelationsfunktion entspricht einem breiten Leistungsdichtespektrum und umgekehrt. - Als Beschreibungsgröße verwenden wir hier die äquivalente LDS-Bandbreite $∇f$ $($man spricht"Nabla-f"$)$, ähnlich definiert wie die äquivalente AKF-Dauer $∇τ$ im Kapitel Interpretation der Autokorrelationsfunktion:
- $${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$
- Mit diesen Definitionen gilt der folgende grundlegende Zusammenhang:
- $${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm bzw.}\hspace{1cm} {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$
$\text{Beispiel 1:}$ Wir gehen von der Grafik oben auf dieser Seite aus:
- Die Kenngrößen des höherfrequenten Signals $x(t)$ sind $∇τ_x = 0.33\hspace{0.08cm} \rm µs$ und $∇f_x = 3 \hspace{0.08cm} \rm MHz$.
- Die äquivalente AKF-Dauer des Signals $y(t)$ ist dreimal so groß: $∇τ_y = 1 \hspace{0.08cm} \rm µs$.
- Die äquivalente LDS-Bandbreite beträgt somit nur mehr $∇f_y = ∇f_x/3 = 1 \hspace{0.08cm} \rm MHz$.
$\text{Allgemein gilt:}$ Das Produkt aus äquivalenter AKF-Dauer ${ {\rm \nabla} \tau_x}$ und äquivalenter LDS-Bandbreite $ { {\rm \nabla} f_x}$ ist immer gleich $1$:
- $${ {\rm \nabla} \tau_x} \cdot { {\rm \nabla} f_x} = 1.$$
$\text{Beweis:}$ Entsprechend den obigen Definitionen gilt:
- $${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac { {\it \Phi}_x(f = {\rm 0)} }{ \varphi_x(\tau = \rm 0)},$$
- $${ {\rm \nabla} f_x} = \frac {1}{ {\it \Phi}_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{ {\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)} }{ {\it \Phi}_x(f = \rm 0)}.$$
Das Produkt ist somit gleich $1$.
$\text{Beispiel 2:}$ Ein Grenzfall des Reziprozitätsgesetzes stellt das so genannte Weiße Rauschen dar:
- Dieses beinhaltet alle Spektralanteile (bis ins Unendliche).
- Die äquivalente LDS-Bandbreite $∇f$ ist unendlich groß.
Das hier angegebene Gesetz besagt, dass damit für die äquivalente AKF-Dauer $∇τ = 0$ gelten muss ⇒ das weiße Rauschen besitzt eine diracförmige AKF.
Mehr zu dieser Thematik finden Sie im dreiteiligen Lernvideo Der AWGN-Kanal, insbesondere im zweiten Teil.
Leistungsdichtespektrum mit Gleichsignalkomponente
Wir gehen von einem gleichsignalfreien Zufallsprozess $\{x_i(t)\}$ aus. Weiter setzen wir voraus, dass der Prozess auch keine periodischen Anteile beinhaltet. Dann gilt:
- Die Autokorrelationsfunktion $φ_x(τ)$ verschwindet für $τ → ∞$.
- Das Leistungsdichtespektrum ${\it \Phi}_x(f)$ – berechenbar als die Fouriertransformierte von $φ_x(τ)$ – ist sowohl wert– als auch zeitkontinuierlich, also ohne diskrete Anteile.
Wir betrachten nun einen zweiten Zufallsprozess $\{y_i(t)\}$, der sich vom Prozess $\{x_i(t)\}$ lediglich durch eine zusätzliche Gleichsignalkomponente $m_y$ unterscheidet:
- $$\left\{ y_i (t) \right\} = \left\{ x_i (t) + m_y \right\}.$$
Die statistischen Beschreibungsgrößen des mittelwertbehafteten Zufallsprozesses $\{y_i(t)\}$ weisen dann folgende Eigenschaften auf:
- Der Grenzwert der AKF für $τ → ∞$ ist nun nicht mehr Null, sondern $m_y^2$. Im gesamten $τ$–Bereich von $–∞$ bis $+∞$ ist die AKF $φ_y(τ)$ um $m_y^2$ größer als $φ_x(τ)$:
- $${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$
- Nach den elementaren Gesetzen der Fouriertransformation führt der konstante AKF-Beitrag im LDS zu einer Diracfunktion $δ(f)$ mit dem Gewicht $m_y^2$:
- $${{\it \Phi}_y ( f)} = {\Phi_x ( f)} + m_y^2 \cdot \delta (f). $$
Nähere Informationen zur Diracfunktion finden Sie im Kapitel Gleichsignal - Grenzfall eines periodischen Signals des Buches „Signaldarstellung”. Weiterhin möchten wir Sie hier auf das Lernvideo Herleitung und Visualisierung der Diracfunktion hinweisen.
Numerische LDS-Ermittlung
Autokorrelationsfunktion und Leistungsdichtespektrum sind über die Fouriertransformation streng miteinander verknüpft. Dieser Zusammenhang gilt auch bei zeitdiskreter AKF-Darstellung mit dem Abtastoperator ${\rm A} \{ \varphi_x ( \tau ) \} $, also für
- $${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$
Der Übergang vom Zeit– in den Spektralbereich kann mit folgenden Schritten hergeleitet werden:
- Der Abstand $T_{\rm A}$ zweier Abtastwerte ist durch die absolute Bandbreite $B_x$ (maximal auftretende Frequenz innerhalb des Prozesses) über das Abtasttheorem festgelegt:
- $$T_{\rm A}\le\frac{1}{2B_x}.$$
- Die Fouriertransformierte der zeitdiskreten (abgetasteten) AKF ergibt ein mit ${\rm 1}/T_{\rm A}$ periodisches LDS:
- $${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$
$\text{Fazit:}$ Da sowohl $φ_x(τ)$ als auch ${\it \Phi}_x(f)$ gerade und reelle Funktionen sind, gilt der Zusammenhang:
- $${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{\infty} \varphi_x ( k T_{\rm A}) \cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
- Das Leistungsdichtespektrum (LDS) des zeitkontinuierlichen Prozesses erhält man aus ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ durch Bandbegrenzung auf den Bereich $\vert f \vert ≤ 1/(2T_{\rm A})$.
- Im Zeitbereich bedeutet diese Operation eine Interpolation der einzelnen AKF-Abtastwerte mit der ${\rm si}$–Funktion, wobei ${\rm si}(x)$ für $\sin(x)/x$ steht.
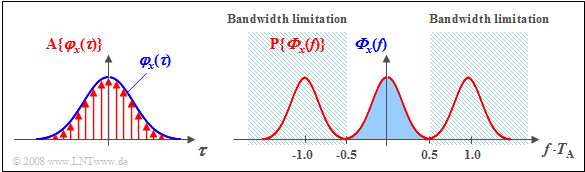
$\text{Beispiel 3:}$ Eine gaußförmige AKF $φ_x(τ)$ wird im Abstand $T_{\rm A}$ abgetastet, wobei das Abtasttheorem erfüllt ist:
- Die Fouriertransformierte der zeitdiskreten AKF ${\rm A} \{φ_x(τ) \}$ sei ${\rm P} \{ { {\it \Phi}_x} ( f) \}$.
- Diese mit ${\rm 1}/T_{\rm A}$ periodische Funktion ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ ist dementsprechend unendlich weit ausgedehnt ( roter Kurvenzug ).
- Das LDS ${\it \Phi}_x(f)$ des zeitkontinuierlichen Prozesses $\{x_i(t)\}$ erhält man durch Bandbegrenzung auf den im Bild blau hinterlegten Frequenzbereich $\vert f · T_{\rm A} \vert ≤ 0.5$.
Genauigkeit der numerischen LDS-Berechnung
Für die nachfolgende Analyse gehen wir von folgenden Annahmen aus:
- Die zeitdiskrete AKF $φ_x(k · T_{\rm A})$ wurde aus $N$ Abtastwerten numerisch ermittelt. Wie bereits auf der Seite Genauigkeit der numerischen AKF-Berechnung gezeigt wurde, sind diese Werte fehlerhaft und die Fehler korreliert, wenn $N$ zu klein gewählt wurde.
- Zur Berechnung des periodischen Leistungsdichtespektrums (LDS) verwenden wir nur die AKF-Werte $φ_x(0)$, ... , $φ_x(K · T_{\rm A})$:
- $${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
$\text{Fazit:}$ Die Genauigkeit der LDS-Berechnung wird im starken Maße durch den Parameter $K$ bestimmt:
- Ist $K$ zu klein gewählt, so werden die eigentlich vorhandenen AKF-Werte $φ_x(k · T_{\rm A})$ mit $k > K$ nicht berücksichtigt.
- Bei zu großem $K$ werden auch solche AKF-Werte berücksichtigt, die eigentlich Null sein sollten und nur wegen der numerischen AKF-Berechnung endlich sind.
- Diese Werte sind allerdings – bedingt durch ein zu kleines $N$ bei der AKF–Ermittlung – nur Fehler, und beinträchtigen die LDS-Berechnung mehr als dass sie einen brauchbaren Beitrag zum Ergebnis liefern.
$\text{Beispiel 4:}$ Wir betrachten hier einen mittelwertfreien Prozess mit statistisch unabhängigen Abtastwerten.
- Deshalb sollte nur der AKF–Wert $φ_x(0) = σ_x^2$ von Null verschieden ist.
- Ermittelt man aber die AKF numerisch aus lediglich $N = 1000$ Abtastwerten, so erhält man auch für $k ≠ 0$ endliche AKF–Werte.
- Das obere Bild zeigt, dass diese fehlerhaften AKF–Werte bis zu $6\%$ des Maximalwertes betragen können.
- Unten ist das numerisch ermittelte Leistungsdichtespektrum dargestellt. Gelb ist der theoretische Verlauf dargestellt, der für $\vert f · T_{\rm A} \vert ≤ 0.5$ konstant sein sollte.
- Die grüne und die violette Kurve verdeutlichen, wie durch $K = 3$ bzw. $K = 10$ das Ergebnis gegenüber $K = 0$ verfälscht wird.
In diesem Fall (statistisch unabhängige Zufallsgrößen) wächst der Fehler monoton mit steigendem $K$. Bei einer Zufallsgröße mit statistischen Bindungen gibt es dagegen jeweils einen optimalen Wert für $K$.
- Wird dieser zu klein gewählt, so werden signifikante Bindungen nicht berücksichtigt.
- Ein zu großer Wert führt dagegen zu Oszillationen, die nur auf fehlerhafte AKF–Werte zurückzuführen sind.
Aufgaben zum Kapitel
Aufgabe 4.12: LDS eines Binärsignals
Aufgabe 4.12Z: Weißes Rauschen