Exercise 4.15: MSK Compared with BPSK and QPSK
Compare the power-spectral densities (in the equivalent low-pass range) of
- Binary Phase Shift Keying $\rm (BPSK)$,
- Quaternary Phase Shift Keying $\rm (QPSK)$,
- Minimum Shift Keying $\rm (MSK)$.
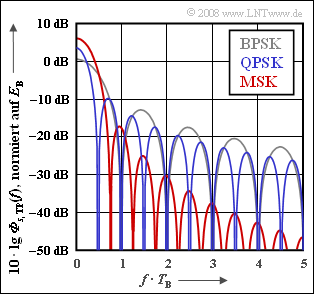
These are shown logarithmically in the graph, with frequency normalized to the reciprocal of the bit duration $T_{\rm B}$ .
For both BPSK and QPSK, a rectangular fundamental pulse of height $s_0$ and symbol duration $T$ is assumed. Thus, for BPSK and QPSK (as well as 4-QAM and offset QPSK), the same applies:
- $${\it \Phi}_{s}(f) = \frac{s_0^2 \cdot T}{4} \cdot \big [ {\rm si}^2 ( \pi T \cdot (f- f_{\rm T}) ) + {\rm si}^2 ( \pi T \cdot (f+ f_{\rm T}) ) \big ]\hspace{0.05cm},$$
and transformed into the equivalent low-pass range:
- $$ {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 ( \pi f T ) \hspace{0.05cm}.$$
Despite having the same formula, BPSK and QPSK have different power-spectral densities:
- In BPSK (grey curve) the symbol duration $T$ is equal to the bit duration $T_{\rm B}$ with an energy per bit of $(E_{\rm B} = s_0^2 · T_{\rm B}/2)$ , it holds that:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = E_{\rm B} \cdot {\rm si}^2 ( \pi f T_{\rm B} ) \hspace{0.05cm}.$$
- In contrast, in QPSK (blue curve) for the same $E_{\rm B}$ , the symbol duration $T$ is doubled:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = 2 \cdot E_{\rm B} \cdot {\rm si}^2 ( 2\pi f T_{\rm B} ) \hspace{0.05cm}.$$
When calculating the MSK spectrum (red curve), one can take into account that MSK can be realized as an offset QPSK as in the block diagram in the theory section if the following fundamental pulse is used:
- $$g(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{for}} \\{\rm{otherwise}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm }\hspace{0.05cm}. \\ \end{array}$$
The corresponding spectral function is calculated in Exercise 4.15Z :
- $$G(f) = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$
Additionally, consider:
- The two signals $s_{\rm I}(t)$ and $s_{\rm Q}(t)$ are uncorrelated despite prior encoding.
- For MSK, contrary to QPSK, one should set $T = T_{\rm B}$ as in BPSK.
- Also, the energy per bit in MSK is given as: $E_{\rm B} = s_0^2 · T/2$.
- The magnitude of the low-pass signal $|s_{\rm TP}(t)| = s_0$ is equal to the maximum value $g_0$ of the fundamental pulse $g(t)$.
Hints:
- This exercise belongs to the chapter Nonlinear Digital Modulation.
- Particular reference is made to the section Realizing MSK as Offset–QPSK.
- The power-spectral density in the equivalent low-pass range of one branch – for example: the in-phase component – is:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = \frac{1}{2 T} \cdot {\rm E} \left [ a_\nu ^2 \right ] \cdot |G(f)|^2 \hspace{0.05cm}.$$
Questions
Solution
(2) Aufgrund der niedrigeren Symbolrate $1/T$ ist bei Quaternary Phase Shift Keying $\rm (QPSK)$ – und bei allen verwandten quaternären Modulationsverfahren – das Spektrum nur halb so breit wie bei der BPSK ⇒ $f_1\hspace{0.15cm}\underline{ =0.5} \cdot 1/T_{\rm B}$.
(3) Für das Leistungsdichtespektrum $\rm (LDS)$ des Gesamtsignals gilt im äquivalenten Tiefpassbereich:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) + {\it \Phi}_{s,\hspace{0.05cm} {\rm Q},\hspace{0.05cm} {\rm TP}}(f)= 2 \cdot {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = {1}/{ T} \cdot |G(f)|^2\hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass
- die Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ unkorreliert sind, so dass man die LDS–Anteile addieren kann,
- wegen der binären bipolaren Amplitudenkoeffizienten der Erwartungswert $E[a_ν^2] = 1$ ist.
Damit erhält man:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{1}{ T} \cdot \left ( \frac {4}{\pi} \right ) ^2 \cdot g_0^2 \cdot T^2 \cdot \frac{ {\rm cos}^2 ( 2 \pi f T )}{ \big [1 - (4 f T)^2 \big ] ^2} \hspace{0.05cm}.$$
Mit $s_0 = g_0$, $T = T_{\rm B}$ und $E_{\rm B} = s_0^2 · T_{\rm B}/2$ gilt weiter:
- $${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{32}{ \pi^2} \cdot E_{\rm B} \cdot \frac{ {\rm cos}^2 ( 2 \pi \cdot f \cdot T_{\rm B} )}{ \big [1 - (4 \cdot f \cdot T_{\rm B})^2 \big ] ^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f = 0 )= \frac{32}{ \pi^2} \cdot E_{\rm B} \hspace{0.15cm}\underline {\approx 3.243 \cdot E_{\rm B}} \hspace{0.05cm}.$$
(4) Richtig ist nur der Lösungsvorschlag 1:
- Bereits aus der Grafik ist zu ersehen, dass die erste Aussage falsch und die zweite richtig ist.
- Der Lösungsvorschlag 3 stimmt ebenfalls nicht. Das Integral über die Leistungsdichtespektren ergibt die Leistung $(E_{\rm B}/T_{\rm B})$.
- Die Signalverläufe von BPSK, QPSK und MSK machen deutlich, dass die Leistung bei konstanter Hüllkurve $(s_0)$ für diese drei Modulationsverfahren gleich ist.