Exercise 3.3: Sum of two Oscillations

Two different Bessel spectra

The equivalent low-pass signal with phase modulation, when normalized to the carrier amplitude $(A_{\rm T} = 1)$ is:

$$ s_{\rm TP}(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}K_{\rm PM}\hspace{0.05cm}\cdot \hspace{0.05cm}q(t) }\hspace{0.05cm},$$

The modulator constant is assumed to be $K_{\rm PM} = \rm 1/V$ throughout the task.

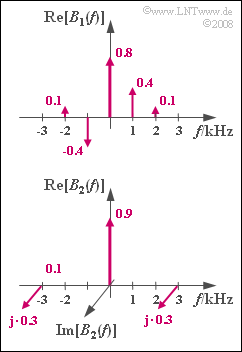
The upper graph shows the corresponding spectral function $B_1(f)$, when the source signal is

$$q_1(t) = 0.9\,{\rm V} \cdot \sin(2 \pi \cdot 1\,{\rm kHz} \cdot t)$$

The weights of the Bessel-Dirac lines when $η_1 = 0.9$ are obtained as follows:

$${\rm J}_0 (0.9) = 0.808 \approx 0.8,\hspace{1cm} {\rm J}_1 (0.9) = 0.406 \approx 0.4,$$

$${\rm J}_2 (0.9) = 0.095 \approx 0.1,\hspace{1cm} {\rm J}_3 (0.9) \approx {\rm J}_4 (0.9) \approx\ \text{ ...} \ \approx 0 \hspace{0.05cm}.$$

Use the approximations given in the graph to simplify the calculations.

The Bessel function $B_2(f)$ is obtained for the source signal

$$q_2(t) = 0.65\,{\rm V} \cdot \cos(2 \pi \cdot 3\,{\rm kHz} \cdot t)$$

The numerical values of the Dirac lines are obtained from the following:

$${\rm J}_0 (0.65) = 0.897 \approx 0.9,\hspace{0.3cm}{\rm J}_1 (0.65) = 0.308 \approx 0.3, \hspace{0.3cm}{\rm J}_2 (0.65) = 0.051 \approx 0\hspace{0.05cm}.$$

From the graph, it can be seen that due to the cosine source signal $q_2(t)$ and the cosine carrier signal $z(t)$ , the spectral lines at $±3 \ \rm kHz$ are both positive and imaginary.

In the context of this task, we will now investigate the case where the source signal

$$q(t) = q_1(t) + q_2(t)$$

is applied to the input of the phase modulator.

It is worth mentioning that $|q(t)| < q_{\rm max} = 1.45 \ \rm V$ .
This maximum value is slightly smaller than the sum $A_1 + A_2$ of the individual amplitudes when a sine and a cosine function with the given amplitudes are added up.

In the following questionnaire,

$S_{\rm TP}(f)$ denotes the spectral function of the equivalent low-pass signal,
$S_+(f)$ denotes the spectral functions of the analytic signal,

in both cases assuming that $q(t) = q_1(t) + q_2(t)$ holds and that the carrier frequency is $f_{\rm T} = 100 \ \rm kHz$ .

Hints:

This exercise belongs to the chapter Phase Modulation.
Particular reference is made to the page Equivalent low-pass signal in phase modulation.
The values of the Bessel functions can be found in formula collections in table form.
You can also use the interactive applet Bessel functions of the first kind to solve this task.

Questions

	The locus curve is an ellipse.
	The locus curve is a circle.
	The locus curve is approximately a semi-circle.
	The locus curve is an arc, with an approximate opening angle of $90^\circ$.

$f_{\rm min} \ = \ $

$\ \rm kHz$

$f_{\rm max} \ = \ $

$\ \rm kHz$

${\rm Re}\big[S_{\rm TP}(f = 0)\big] \ = \ $

${\rm Im}\big[S_{\rm TP}(f = 0)\big] \ = \ $

${\rm Re}\big[S_{\rm TP}(f = 1 \ \rm kHz)\big] \ = \ $

${\rm Im}\big[S_{\rm TP}(f = 1 \ \rm kHz)\big] \ = \ $

${\rm Re}\big[S_{\rm +}(f = 98 \ \rm kHz)\big] \ = \ $

${\rm Im}\big[S_{\rm +}(f = 98 \ \rm kHz)\big] \ = \ $

Solution

(1) The third answer is correct:

In angle modulation, the complex pointer $s_{\rm TP}(t)$ always moves on a circular arc with the following opening angle:

$$2 · K_{\rm PM} · q_{\rm max} = 2 \cdot {\rm 1/V} \cdot 1.45 \ \rm V = 2.9 \ \rm rad \approx 166^\circ.$$

Using the (admittedly very rough) approximation $166^\circ \approx 180^\circ$ we indeed get a semicircle.

(2) In general, $S_{\rm TP}(f) = B_1(f) ∗ B_2(f)$ holds.

Since $B_1(f)$ is limited to the frequencies $|f| ≤ 2 \ \rm kHz$ and $B_2(f)$ is limited to the range $±3 \ \rm kHz$ , the convolution product is limited to $|f| ≤ 5 \ \rm kHz$ .
It follows that:

$$f_{\rm min} \hspace{0.15cm}\underline {= -5 \ \rm kHz},$$

$$f_{\rm max} \hspace{0.15cm}\underline {=+5 \ \rm kHz}.$$

(3) The convolution product for frequency $f = 0$ results from multiplying $B_1(f)$ with $B_2(f)$ and summing.

Only for $f = 0$ are both $B_1(f)$ and $B_2(f)$ non-zero.
Thus, we get:

$$ S_{\rm TP}(f = 0) = B_{1}(f = 0) \cdot B_{2}(f = 0)= 0.8 \cdot 0.9 \hspace{0.15cm}\underline {= 0.72}\hspace{0.2cm}{\rm (rein \hspace{0.15cm} reell)} \hspace{0.05cm}.$$

(4) Now, before multiplication and summation there needs to be a frequency shift of $B_2(f)$ to the right – or of $B_1(f)$ to the left– by $1 \ \rm kHz$ erfolgen. This gives:

$$S_{\rm TP}(f = 1\,{\rm kHz}) = B_{1}(f = -2\,{\rm kHz}) \cdot B_{2}(f = 3\,{\rm kHz}) + B_{1}(f = 1\,{\rm kHz}) \cdot B_{2}(f = 0) = 0.1 \cdot {\rm j} \cdot 0.3 + 0.4 \cdot 0.9\hspace{0.15cm} = 0.36 + {\rm j} \cdot 0.03$$

$$\Rightarrow \hspace{0.3cm} {\rm Re}[S_{\rm TP}(f = 1\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.36} \hspace{0.05cm},\hspace{0.3cm} {\rm Im}[S_{\rm TP}(f = 1\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.03} \hspace{0.05cm}.$$

(5) The Dirac line $S_+(f = 98 \ \rm kHz)$ corresponds to the $S_{\rm TP}(f)$–line at $f = -2 \ \rm kHz$. This is

$$S_{\rm TP}(f \hspace{-0.05cm}=\hspace{-0.05cm} -2\,{\rm kHz}) \hspace{-0.03cm}=\hspace{-0.03cm} B_{1}(f = -2\,{\rm kHz}) \cdot B_{2}(f \hspace{-0.05cm}=\hspace{-0.05cm} 0) + B_{1}(f \hspace{-0.05cm}=\hspace{-0.05cm} 1\,{\rm kHz}) \cdot B_{2}(f \hspace{-0.05cm}=\hspace{-0.05cm} -3\,{\rm kHz})= 0.1 \cdot 0.9 + 0.4 \cdot {\rm j} \cdot 0.3 \hspace{0.15cm}\hspace{-0.03cm}=\hspace{-0.03cm} 0.09 + {\rm j} \cdot 0.12$$

$$\Rightarrow \hspace{0.3cm} {\rm Re}[S_{\rm +}(f = 98\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.09} \hspace{0.05cm}, \hspace{0.3cm} {\rm Im}[S_{\rm +}(f = 98\,{\rm kHz})] \hspace{0.15cm}\underline {= 0.12} \hspace{0.05cm}.$$