Exercise 3.7: Angular Modulation of a Harmonic Oscillation

Demodulator
for FM

The signal arriving at a receiver is:

$$ r(t) = 3\,{\rm V} \cdot \cos \hspace{-0.05cm} \big[2 \pi \cdot 1\,{\rm MHz} \cdot t + 3 \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\big]\hspace{0.05cm}.$$

$r(t)$ is an angle-modulated signal that was neither distorted nor influenced by noise during transmission.

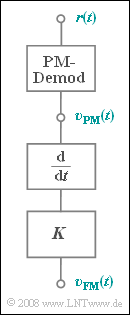
The signals $v_{\rm PM}(t)$ and $v_{\rm FM}(t)$ result after ideal demodulation by means of

a phase demodulator, given by the equation

$$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$

a frequency demodulator, consisting of a PM demodulator, a differentiator and a constant $K$.

In order for all signals to have equal units, this constant $K$ is dimensionally constrained.

Hints:

This exercise belongs to the chapter Frequency Modulation.
Reference is also made to the chapter Phase Modulation and particularly to the section Signal characteristics with frequency modulation.

Questions

	There could be a PM modulation.
	There could be a FM modulation.
	The message phase is definitely $ϕ_{\rm N} = 0$.
	The message phase is definitely $f_{\rm N} = 10 \ \rm kHz$.

$v_{\rm PM}(t = 0) \ = \ $

$\ \rm V$

$ϕ_{\rm N} \ = \ $

$\ \rm Grad$

$K\ = \ $

$\ \rm \cdot 10^4 \ 1/s$

	The phase deviation is $ϕ_{\rm max} = 3$.
	The frequency deviation is $Δf_{\rm A} = 30 \ \rm kHz$.
	Instantaneous frequencies between $0.97\ \rm MHz$ And $1.03 \ \rm MHz$ .
	If $f_{\rm N} = 5 \ \rm kHz$ , the phase deviation would be unchanged.
	If $f_{\rm N} = 5 \ \rm kHz$ the frequency deviation would be unchanged.

Solution

(1) Answers 1, 2 and 4 are correct:

From the eqution for $r(t)$ it can only be acertained that it is an angle modulation,
but not whether it is a phase modulation (PM) or a frequency modulation (FM).
Based on the equation, it is clear that the message frequency is $f_{\rm N} = 10 \ \rm kHz$ .
The phase $ϕ_{\rm N} = 0$ of the source signal would then only apply, if phase modulation were present.

(2) With the modulator constant $K_{\rm PM} = 2 \ \rm V^{–1}$ this is given by:

$$v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) = \frac{3}{2\,{\rm V}^{-1}} \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$

At time $t = 0$ it therefore holds that:

$$v_{\rm PM}(t = 0) = {A_{\rm N}} \hspace{0.15cm}\underline {= 1.5\,{\rm V}}\hspace{0.05cm}.$$

(3) The output signal $v_{\rm FM}(t)$ of the FM demodulator – consisting of a PM–demodulator and differentiator – can be written as:

$$v_{\rm FM}(t) = \frac{{\rm d}v_{\rm PM}(t)}{{\rm d}t} \cdot K = \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot (- \sin(2 \pi \cdot {f_{\rm N}} \cdot t))= \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot \cos(2 \pi \cdot {f_{\rm N}} \cdot t + 90^\circ)\hspace{0.05cm}.$$

The message phase is thus $ϕ_{\rm N} \hspace{0.15cm}\underline {= 90^\circ}$.

(4) In this case, it must hold that:

$$ K ={2 \pi \cdot f_{\rm N}} \hspace{0.15cm}\underline { = 6.28 \cdot 10^{4} \,\,{1}/{ s}} \hspace{0.05cm}.$$

(5) Answers 1, 2, 3 and 5 are correct:

The phase deviation is identical to the modulation index, which can be discerned from the equation given:

$$\phi_{\rm max} = \eta = 3 = \frac{\Delta f_{\rm A}}{ f_{\rm N}} \hspace{0.05cm}.$$

This leads to the frequency deviation $Δf_{\rm A} = 3 · f_{\rm N} = 30 \ \rm kHz$.
With a carrier frequency of $f_{\rm T} = 1 \ \rm MHz$ , the instantaneous frequency $f_{\rm T}(t)$ can only take values between $1±0.03 \ \rm MHz$ .

Thus, the following statement is also valid::

At half the message frequency, the phase deviation $η$ doubles, while the frequency deviation $Δf_{\rm A}$ is unaffected:

$$\eta = \frac{K_{\rm PM} \cdot A_{\rm N}}{ f_{\rm N}} = 6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} = \eta \cdot f_{\rm N} = 6 \cdot 5\,{\rm kHz} = 30\,{\rm kHz}\hspace{0.05cm}.$$