Exercise 1.10Z: Gaussian Band-Pass
For this exercise we assume:
- Binary phase modulation (BPSK) is used for modulation.
- Demodulation is frequency and phase synchronous.
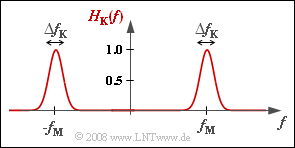
For carrier frequency modulated transmission, the channel frequency response $H_{\rm K}(f)$ must always be assumed to be a bandpass. The channel parameters are, for example, the center frequency $f_{\rm M}$ and the bandwidth $\Delta f_{\rm K}$, where the center frequency $f_{\rm M}$ often coincides with the carrier frequency $f_{\rm T}$.
In this exercise, in particular, we will assume a Gaussian bandpass according to the diagram. For its frequency response holds:
- $$H_{\rm K}(f) = {\rm exp} \left [ - \pi \cdot \left ( \frac {f - f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ] +{\rm exp} \left [ - \pi \cdot \left ( \frac {f + f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ]$$
For a simpler description, one often uses the equivalent TP frequency response $H_{\rm K,TP}(f)$. This results from $H_{\rm K}(f)$ by
- truncating the components at negative frequencies,
- shifting the spectrum by $f_{\rm T}$ to the left.
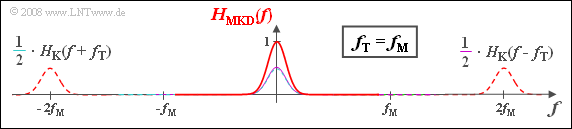
In the considered example with $f_{\rm T} = f_{\rm M}$ for the equivalent TP frequency response results:
- $$ H_{\rm K,\hspace{0.04cm} TP}(f) = {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {f }/{\Delta f_{\rm K}}\right )^2 }.$$
The corresponding time function (Fourier inverse transform) is:
- $$ h_{\rm K,\hspace{0.04cm} TP}(t) = \Delta f_{\rm K} \cdot {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {\Delta f_{\rm K}} \cdot t \right )^2 }.$$
However, the frequency response is also suitable for describing a phase-synchronous BPSK system in the low-pass range
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] ,$$
where "MKD" stands for modulator – channel (Kanal) – demodulator. Often - but not always - $H_{\rm MKD}(f)$ and $H_{\rm K,TP}(f)$ are identical.
Notes:
- The exercise belongs to the chapter Linear Digital Modulation - Coherent Demodulation.
- Reference is made in particular to the section Baseband model for ASK and BPSK.
Questions
Solution
- $$H_{\rm K}(f) = H_{\rm K,\hspace{0.04cm} TP}(f) \star \big [ \delta (f - f_{\rm M}) + \delta (f + f_{\rm M}) \big ] .$$
- The Fourier inverse transform of the bracket expression yields a cosine function of frequency $f_{\rm M}$ with amplitude $2$.
- Thus, according to the convolution theorem:
- $$h_{\rm K}(t) = 2 \cdot \Delta f_{\rm K} \cdot {\rm exp} \left [ - \pi \cdot \left ( {\Delta f_{\rm K}} \cdot t \right )^2 \right ] \cdot \cos(2 \pi f_{\rm M} t ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm K}(t = 0)/\Delta f_{\rm K} \hspace{0.1cm}\underline {= 2}.$$
- This means: The TP impulse response $h_{\rm K,\hspace{0.04cm}TP}(t)$ is identical in shape to the envelope of the bp impulse response $h_{\rm K}(t)$, but twice as large.
(2) Statements 2, 3 and 4 are correct:
- The first statement is false because $H_{\rm MKD}(f)$ also has components around $\pm 2f_{\rm T}$.
- The time function $h_{\rm K,\hspace{0.04cm}TP}(t)$ is real according to the given equation.
- The same is true for $h_{\rm MKD}(t)$ also considering the $\pm 2f_{\rm T}$ components, since $H_{\rm MKD}(f)$ is an even function with respect to $f = 0$.
- The diagram shows $H_{\rm MKD}(f)$, which also has components around $\pm 2f_{\rm T}$. At low frequencies, $H_{\rm K,\hspace{0.04cm}TP}(f)$ is identical to $H_{\rm MKD}(f)$.
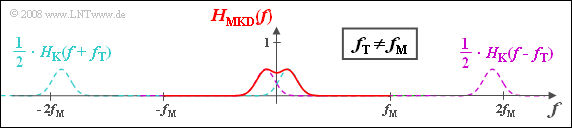
(3) Only solution 4 is correct:
- Here $H_{\rm K,\hspace{0.04cm}TP}(f)$ and $H_{\rm MKD}(f)$ differ even at the low frequencies.
- $H_{\rm K,\hspace{0.04cm}TP}(f)$ is a Gaussian function with the maximum at $f_{ε} = f_{\rm M} - f_{\rm T}$.
- Because of this asymmetry, $h_{\rm K,\hspace{0.04cm}TP}(t)$ is complex.
- In contrast, $H_{\rm MKD}(f)$ is still an even function with respect to $f = 0$ with real impulse response $h_{\rm MKD}(t)$.
- $H_{\rm MKD}(f)$ is composed of two Gaussian functions at $± f_ε$.
(4) Correct is of course the first answer.