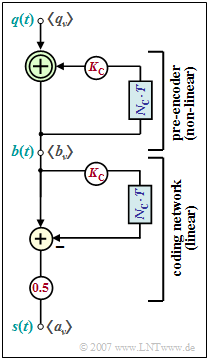
The diagram shows the block diagram for AMI coding, assuming binary bipolar amplitude coefficients $q_{\nu} ∈ \{–1, +1\}$ at the input. This recoding is done in two stages:
- In the first part of the block diagram, a binary precoded symbol $b_{\nu}$ is generated at each clock step from the modulo-2 addition of $q_{\nu}$ and $b_{\nu -1}$. It holds $b_{\nu} ∈ \{–1, +1\}.$
- Then, the current amplitude coefficient of the ternary transmitted signal $s(t)$ is determined by a conventional subtraction. Thereby holds:
- $$a_\nu = {1}/{2} \cdot \left [ b_\nu - b_{\nu-1} \right ] \hspace{0.05cm}.$$
Due to AMI coding, it is ensured that no long "$+1$"– or "$–1$" sequences are created. Modified AMI codes have also been developed to avoid long zero sequences:
- In the HDB3 code, four consecutive zeros each are marked by a specific violation of the AMI coding rule.
- In the B6ZS code, six consecutive zeros are marked by a targeted violation of the AMI coding rule.
The power-spectral density ${\it \Phi}_{a}(f)$ of the amplitude coefficients is to be obtained from the discrete ACF values $\varphi_{a}(\lambda) = {\E}\big[a_{\nu} \cdot a_{\nu + \lambda}\big]$. The Fourier transform in discrete representation is:
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Symbol-Wise Coding with Pseudo Ternary Codes".
- You can check the results with the interactive applet "Signals, ACF and PSD of pseudo ternary codes".
Questions
Solution
- It is $b_{\nu} = +1$ if $q_{\nu}$ and $b_{\nu – 1}$ differ, otherwise set $b_{\nu} = -1$.
- With the initial value $b_{0} = -1$ we obtain:
- $$b_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} b_2 = +1, \hspace{0.2cm}b_3 = -1, \hspace{0.2cm}b_4 = +1, \hspace{0.2cm}b_5 = +1, \hspace{0.2cm}b_6 = -1\hspace{0.05cm},$$
- $$b_7 = +1, \hspace{0.2cm} b_8 = +1, \hspace{0.2cm}b_9 = +1, \hspace{0.2cm}b_{10} = +1, \hspace{0.2cm}b_{11} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}b_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$
(2) AMI coding gives the following amplitude coefficients:
- $$a_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} a_2 = 0, \hspace{0.2cm}a_3 = -1, \hspace{0.2cm}a_4 = +1, \hspace{0.2cm}a_5 = 0, \hspace{0.2cm}a_6 = -1\hspace{0.05cm},$$
- $$a_7 = +1, \hspace{0.2cm} a_8 = 0, \hspace{0.2cm}a_9 = 0, \hspace{0.2cm}a_{10} = 0, \hspace{0.2cm}a_{11}\hspace{0.15cm}\underline { = 0}, \hspace{0.2cm}a_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$
This result is obtained by the equation $a_{\nu} = (b_{\nu} - b_{\nu –1})/2$ or by direct application of the AMI coding rule:
- A source symbol $q_{\nu} = -1$ always leads to $a_{\nu} = 0$.
- Source symbols $q_{\nu} = +1$ lead alternately to $a_{\nu} = +1$ and $a_{\nu} = -1$.
(3) Solution 1 is correct:
- The AMI code yields four consecutive zeros in the range between $\nu = 8$ and $\nu = 11$.
- In the HDB3 code, these four symbols would be marked with "$+ 0 0 +$". Thus, the AMI rule is deliberately violated for identification purposes.
- In contrast, the B6ZS code substitutes only zero sequences over six symbols.
(4) Assuming equally probable binary values $±1$, we obtain ${\Pr}(a_{\nu} = 0) = {\Pr}(q_{\nu} = -1)\hspace{0.15cm}\underline{ = 1/2}$ and for symmetry reasons
- ${\Pr}(a_{\nu} = +1) = {\Pr}(a_{\nu} = -1) \hspace{0.15cm}\underline{ = 1/4}.$
(5) Using the probabilities calculated in (4), we obtain:
- $${\rm E}\big[a_\nu \big] = \ {1}/{4} \cdot (+1) +{1}/{2} \cdot 0+ {1}/{4} \cdot (-1)\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$
- $$ {\rm E}\big[a_\nu^2 \big] = \ {1}/{4} \cdot (+1)^2 +{1}/{2} \cdot 0^2 + {1}/{4} \cdot (-1)^2 \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
(6) The ACF value at $\lambda = 0$ is equal to the root mean square of the amplitude coefficients:
- $$ \varphi_a(\lambda = 0) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
- Since the order of the AMI code is $N = 1$, for $\lambda > 1$: $\varphi_a(\lambda > 1) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$
- The ACF value $\varphi_{a}(\lambda = 1)$ must be determined by averaging: $\varphi_a(\lambda = 1) = {\rm E}[a_\nu \cdot a_{\nu+1} \cdot {\rm Pr}(a_\nu \cap a_{\nu+1})] \hspace{0.05cm}.$
- Of the nine possible combinations for $a_{\nu} \cdot a_{\nu +1}$, only four yield a nonzero value. In the other cases, either $a_{\nu} = 0$ or $a_{\nu +1} = 0$.
However, since in AMI code also
- $${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= +1)] = \ 0 \hspace{0.05cm},$$
- $$ {\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= -1)] = \ 0$$
is true,
- $${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= -1)] = \ {\rm Pr}(a_\nu = +1)\cdot {\rm Pr}(a_{\nu+1} = -1 | a_\nu = +1) = {1}/{4}\cdot{1}/{2} ={1}/{8} \hspace{0.05cm},$$
- $${\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= +1)] = \ {\rm Pr}(a_\nu = -1)\cdot {\rm Pr}(a_{\nu+1} = +1 | a_\nu = -1) = {1}/{4}\cdot {1}/{2} = {1}/{8}$$
is obtained as the final result (since the ACF is always an even function):
- $$\varphi_{a}(\lambda = +1) = \varphi_{a}(\lambda = –1) = –0.25.$$
- This takes into account that $a_{\nu} = +1$ is followed by $a_{\nu +1} = +1$ and $a_{\nu +1} = -1$ with equal probability.
- Thus, the result is:
- $$\varphi_a(\lambda = 0)\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}, $$
- $$\varphi_a(\lambda = 1)\hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm},$$
- $$\varphi_a(\lambda = 2)\hspace{0.15cm}\underline {= 0}.$$
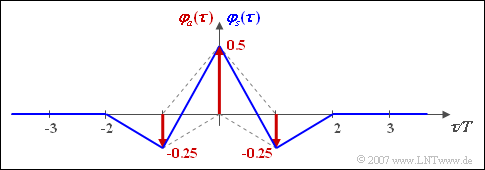
The graph shows
- the discrete ACF $\varphi_{a}(\lambda)$ of the amplitude coefficients and
- the ACF $\varphi_{s}(\tau)$ of the transmitted signal under the condition of NRZ rectangular pulses and AMI coding.
Here, the ACF $\varphi_{s}(\tau)$ drawn in blue is the result of the (discrete) convolution between the discrete ACF $\varphi_{a}(\lambda)$ – drawn in red – and the triangular energy ACF of the basic transmission pulse.
(7) From the given equation, taking into account the discrete ACF values calculated in (6)
- $$\varphi_{a}(\lambda = 0) = 1/2,$$
- $$\varphi_{a}(|\lambda| = 1) = -1/4,$$
- $$\varphi_{a}(|\lambda| > 1) = 0$$
we obtain the following result:
- $${\it \Phi}_a(f) = \ \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(\lambda = 0) + 2 \cdot \varphi_a(\lambda = 1 )\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) = \ {1}/{2} \cdot \left [ 1 - \cos ( 2 \pi f \hspace{0.02cm} T)\right ] = \sin^2 ( \pi f \hspace{0.02cm} T) \hspace{0.05cm}.$$
In particular, holds:
- $${\it \Phi}_a(f = 0) \hspace{0.15cm}\underline {= 0},$$
- $${\it \Phi}_a(f = {1}/({2T})) = \sin^2 ({\pi}/{2})\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$