Übertragungsmaß von Koaxialkabeln
Koaxialkabel bestehen aus einem Innenleiter und – durch ein Dielektrikum getrennt – einem Außenleiter. Es wurden zwei unterschiedliche Kabeltypen standardisiert, wobei zur Kennzeichnung die Durchmesser von Innen– und Außenleiter herangezogen werden:
- das Normalkoaxialkabel, dessen Innenleiter einen Durchmesser von 2.6 mm besitzt und der Außendurchmesser 9.5 mm beträgt,
- das Kleinkoaxialkabel mit den Abmessungen 1.2 mm und 4.4 mm.
Der Kabelfrequenzgang $H_{\rm K}(f)$ ergibt sich aus der Kabellänge $l$ und dem Übertragungsmaß
$$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot (\beta_1 \cdot f + \beta_2 \cdot \sqrt {f})\hspace{0.05cm}$$
$$\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{-\gamma(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{-\alpha(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.05cm}.$$
Die kabelspezifischen Konstanten für das Normalkoaxialkabel 2.6/9.5 mm sind:
$$\begin{align*}\alpha_0 & = 0.00162\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000435\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 21.78\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$
Entsprechend lauten die kilometrischen Dämpfungs– und Phasenkonstanten für das Kleinkoaxialkabel: $$\begin{align*}\alpha_0 & = 0.00783\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000443\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.5984\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 22.18\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.5984\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$
Diese Werte können aus den geometrischen Abmessungen der Kabel berechnet werden und wurden durch Messungen am Fernmeldetechnischen Zentralamt in Darmstadt bestätigt – siehe $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=entitaet&e_id=29656&hyperlink_typ=entitaet_verweis&session_id=7761LSYGTN1463149483}{[Wel77]}$. Sie gelten für eine Temperatur von 20°C (293 K) und Frequenzen größer als 200 kHz. Es besteht folgender Zusammenhang zu den $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=2433&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=7761LSYGTN1463149483}{Leitungsbelägen}$:
- Die vom frequenzunabhängigem Anteil $R’$ herrührenden Ohmschen Verluste werden durch $α_0$ modelliert und verursachen eine (bei Koaxialkabeln geringe) frequenzunabhängige Dämpfung.
- Der Anteil $α_1 · f$ des Dämpfungsmaßes ist auf die Ableitungsverluste $(G’)$ zurückzuführen und der frequenzproportionale Term $β_1 · f$ bewirkt nur eine Phasenlaufzeit, aber keine Verzerrungen.
- Die Anteile $α_2$ und $β_2$ gehen auf den Skineffekt zurück, der bewirkt, dass bei höherfrequentem Wechselstrom die Stromdichte im Leiterinneren niedriger ist als an der Oberfläche. Dadurch steigt der Widerstandsbelag $R’$ einer elektrischen Leitung mit der Wurzel aus der Frequenz an.
Charakteristische Kabeldämpfung (1)
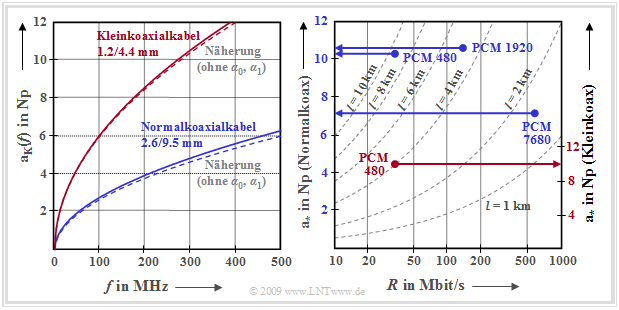
Wir betrachten zunächst die linke Grafik; das rechte Diagramm wird weiter unten beschrieben. Links dargestellt ist das Dämpfungsmaß der zwei Koaxialkabeltypen im Frequenzbereich bis 500 MHz: $${\rm a}_{\rm K}(f) =\left [ \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f} \hspace{0.05cm} \right ] \cdot l \hspace{0.05cm}.$$ Die Ordinatenbeschriftung ist hierbei in Np/km angegeben. Oft erfolgt sie auch in dB/km, wobei die Umrechnung 1 dB = ln(10)/20 = 0.11513 Np gilt.
Man erkennt aus dieser Darstellung, dass der Fehler bei Vernachlässigung des frequenzunabhängigen Anteils $α_0$ und des frequenzproportionalen Terms $(α_1f)$ noch tolerabel ist. Im Folgenden gehen wir deshalb von der folgenden vereinfachten Dämpfungsfunktion aus: $${\rm a}_{\rm K}(f) = \alpha_2 \cdot \sqrt {f} \cdot l = {\rm a}_{\rm \star}\cdot \sqrt { {2f}/{R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{- {\rm a}_{\rm K}(f)}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm K}(f)\hspace{0.15cm}{\rm in }\hspace{0.15cm}{\rm Np}\hspace{0.05cm}.$$
Beachten Sie, dass das Dämpfungsmaß mit „alpha” bezeichnet wird und die Dämpfungsfunktion (nach Multiplikation mit der Länge) mit „a” , was beim verwendeten Zeichensatz schwer zu erkennen ist.
Die charakteristische Kabeldämpfung $a_∗$ eignet sich insbesondere für den Vergleich verschiedener leitungsgebundener Übertragungssysteme mit unterschiedlichen Bitraten $(R)$, Kabeltypen (zum Beispiel Normal– oder Kleinkoaxialkabel) und Kabellängen $l$. Bei all diesen Übertragungssystemen beschreibt $a_∗$ die Dämpfung bei der halben Bitrate unter Vernachlässigung des $α_0$ – und des $α_1$ –Terms: $${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R}/{2}) = \alpha_2 \cdot \sqrt {{R}/{2}} \cdot l\hspace{0.05cm}.$$ Die Beschreibung des rechten Diagramms folgt anschließend.