Exercise 1.14: Bhattacharyya Bound for BEC

Possible received vectors for the $(5, 2)$ code and BEC

In this exercise, we consider the systematic $(5, 2)$ code

with the $2×5$ generator matrix

$${ \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},$$

the $3 × 5$ parity-check matrix

$${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},$$

and the $2^k = 4$ code words

$$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$

At the output of the digital channel defined by the BEC model (Binary Erasure Channel) with the erasure probability $\lambda = 0.001$ the received vector

$$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$

occurs, where for $i = 1, \ \text{...} \ , 5$ holds: $y_{i} \in \{0, 1, \rm E\}$.

The BEC channel is characterized by the fact that.

corruptions $(0 → 1, 1 → 0)$ are excluded,
but cancellations $(0 → \rm E, 1 → E)$ may occur.

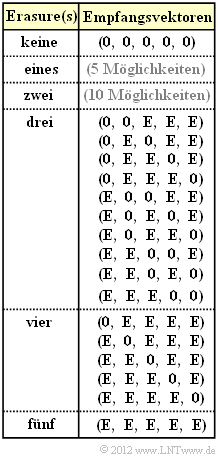
The graph explicitly shows all possible received vectors $\underline{y}$ with three or more erasures $\rm E$ assuming that the all-zero vector $(0, 0, 0, 0, 0)$ was sent.

For less than three extinctions, for the considered $(5, 2)$ code, the codeword finder always returns the correct decision: $\underline{z} = \underline{x}$.

On the other hand, if there are three or more erasures, wrong decisions may occur. In this case, the following applies to the block error probability:

$$ {\rm Pr(block\:error)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$

Please note:

The event $[\underline{x}_{0} → \underline{x}_{1}]$ does not necessarily say that at the received vector under consideration $\underline{y}$ is actually decided for the codeword $\underline{x}_{1}$ is decided, but only that the decision for $x_{1}$ would be more reasonable than the decision for $\underline{x}_{0}$ due to statistics.
But it could also be decided for $\underline{x}_{2}$ or $\underline{x}_{3}$ if the maximum-likelihood criterion is in favor.

Die Berechnung der Blockfehlerwahrscheinlichkeit ist schwierig, da die Ereignisse $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ und $[\underline{x}_{0} → \underline{x}_{3}]$ nicht notwendigerweise disjunkt sind. Eine obere Schranke liefert die Union Bound:

$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$

Eine weitere Schranke wurde von Bhattacharyya angegeben:

$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(Blockfehler)} \hspace{0.05cm},$$

wobei beim Binary Erasure Channel für den Bhattacharyya–Parameter $\beta = \lambda$ gilt und $W(X)$ die Gewichtsfunktion angibt, wobei die Pseudo–Variable $X$ hier durch den Bhattacharyya–Parameter $\lambda$ zu ersetzen ist.

Die Bhattacharyya–Schranke liegt je nach Kanal mehr oder weniger weit oberhalb der Union Bound.
Ihre Bedeutung liegt darin, dass die Schranke für unterschiedliche Kanäle in gleicher Weise angebbar ist.

Hinweis:

Die Aufgabe gehört zum Kapitel Schranken für die Blockfehlerwahrscheinlichkeit.

Fragebogen

${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}] \ = \ $

$\ \cdot 10^{-3} $

	Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ \lambda ^{d_{{\rm H},\hspace{0.05cm}i}} \ · \ (1 – \lambda)^{n \hspace{0.05cm}– \hspace{0.05cm}d_{{\rm H},\hspace{0.05cm}i}}$.
	Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ 1/2 · \lambda ^{d_{{\rm H},\hspace{0.05cm}i}}.$
	${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ ist die Verfälschungswahrscheinlichkeit von $x_{0}$ nach $x_{i}$.

$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{2}] \ = \ $

$\ \cdot 10^{-3} $

$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}] \ = \ $

$\ \cdot 10^{-3} $

$\ {\rm Pr(Union\ Bound)} \ = \ $

$\ \cdot 10^{-3} $

$\ {\rm Pr(Bhattacharyya)} \ = \ $

$\ \cdot 10^{-3} $

Musterlösung

Solution

(1) Die Codeworte $\underline{x}_{0}$ und $\underline{x}_{1}$ unterscheiden sich in Bit $2, \ 4$ und $5$. Wird nur einer dieser drei Binärwerte richtig übertragen, ist damit das gesamte Codewort eindeutig bestimmt. Keine Information über das Codewort erhält man bei folgenden Empfangsvektoren (siehe Tabelle auf der Angabenseite):

$\underline{y} = (0, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^3 \ · \ (1 – \lambda)^2$,
$\underline{y} = (0, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$,
$\underline{y} = ({\rm E}, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$,
$\underline{y} = ({\rm E}, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^5$.

Die Wahrscheinlichkeit, dass aufgrund des spezifischen Empfangsvektors $\underline{y}$ das Codewort $\underline{x}_{1}$ genau so wahrscheinlich ist wie $\underline{x}_{0}$, ergibt sich zu

$$\ {\rm Pr}\ [\underline{x}_0 \hspace{0.12cm}{\rm und}\hspace{0.12cm} \underline{x}_1 \hspace{0.15cm}{\rm sind \hspace{0.15cm}gleichwahrscheinlich}] = \lambda^3 \cdot (1- \lambda)^2 + 2 \cdot \lambda^4 \cdot (1- \lambda) + \lambda^5 =\lambda^3 \cdot \left [ (1- \lambda)^2 + 2 \cdot \lambda \cdot (1- \lambda) + \lambda^2 \right ] = \lambda^3 \hspace{0.05cm}.$$

In diesem Fall entscheidet man sich nach dem Zufallsprinzip für $\underline{x}_{0}$ (wäre richtig) oder für $\underline{x}_{1}$ (leider falsch), und zwar mit gleicher Wahrscheinlichkeit. Daraus folgt:

$${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm}.$$

(2) Nach Teilaufgabe (1) ist die Antwort 2 richtig und nicht die Antwort 1. Auch die Aussage 3 ist falsch:

${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht aus, dass mit dieser Wahrscheinlickeit das Codewort $\underline{x}_{0}$ tatsächlich in das falsche Codewort $\underline{x}_{1}$ übergeht, sondern nur, dass es mit dieser Wahrscheinlichkeit zu $\underline{x}_{1}$ übergehen könnte.
${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ beinhaltet auch Konstellationen, bei denen die Entscheidung tatsächlich für $\underline{x}_{2}$ bzw. $\underline{x}_{3}$ fällt.

(3) Wegen $d_{\rm H}(\underline{x}_{0}, \underline{x}_{2}) = 3$ und $d_{\rm H}(\underline{x}_{0}, \underline{x}_{3}) = 4$ ergibt sich hierfür

$${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm},\hspace{0.2cm} {\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] = 1/2 \cdot \lambda^4 \hspace{0.15cm} \underline{= 0.05 \cdot 10^{-3}} \hspace{0.05cm}.$$

(4) Die Blockfehlerwahrscheinlichkeit ist nie größer (mit einer gewissen Wahrscheinlichkeit eher kleiner) als die so genannte Union Bound:

$${\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] = 2 \cdot \lambda^3/2 + \lambda^4/2 = 0.001 + 0.00005 \hspace{0.15cm} \underline{= 1.05 \cdot 10^{-3}} \hspace{0.05cm}.$$

(5) Allgemein gilt:

$${\rm Pr(Blockfehler) ≤ {\rm Pr(Union \hspace{0.15cm}Bound)} \le Pr(Bhattacharyya)} = W(\beta) - 1.$$

Für das Distanzspektrum bzw. die Gewichtsfunktion erhält man im vorliegenden Fall:

$$W_0 = 1 \hspace{0.05cm}, \hspace{0.2cm} W_3 = 2 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(X) = 1+ 2 \cdot X^{3} +X^{4} \hspace{0.05cm}.$$

Beim BEC–Kanal gilt zudem $\beta = \lambda$. Daraus folgt als Endergebnis für $\lambda = 0.001$:

$${\rm Pr(Bhattacharyya)} = 2 \cdot \lambda^3 + \lambda^4 \hspace{0.15cm} \underline{= 2.1 \cdot 10^{-3}} \hspace{0.05cm}.$$

Anzumerken ist, dass beim BEC–Modell die Bhattacharyya–Schranke stets doppelt so groß ist wie die Union Bound, die ja selbst wieder eine obere Schranke für die Blockfehlerwahrscheinlichkeit darstellt.