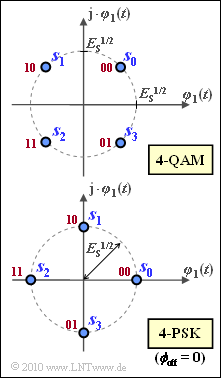
Exercise 4.14Z: 4-QAM and 4-PSK

Signal space constellation of 4-QAM and 4-PSK

For "quadrature amplitude modulation" ($M$–QAM), an upper bound ("Union–Bound") on the symbol error probability was given in the theory section for $M ≥ 16$:

$$ p_{\rm UB} = 4 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$

In the theory section, one can also find the "Union–Bound" for "M–level phase modulation" (M–PSK)

$$ p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$

Bei beiden Verfahren hat jeder Signalraumpunkt die genau gleiche Energie, nämlich $E_{\rm S}$.

Aus der Grafik erkennt man, dass für den Sonderfall $M = 4$ die beiden Modulationsverfahren eigentlich identisch sein müssten, was aus den obigen Gleichungen nicht direkt hervorgeht.

Die 4–PSK ist hier mit dem Phasenoffset $\phi_{\rm off} = 0$ dargestellt. Mit einem allgemeinen Phasenoffset lauten dagegen die Inphase– und Quadraturanteile der Signalraumpunkte allgemein: $(i = 0, \ ... \ , M = 1)$:

$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$

$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$

Hinweise:

Die Aufgabe gehört zum Kapitel "Carrier Frequency Systems with Coherent Demodulation".
Bezug genommen wird insbesondere auf die Seiten Quadraturamplitudenmodulation und Mehrstufige Phasenmodulation.
In der obigen Grafik rot eingezeichnet ist die Gray–Zuordnung der Symbole zu Bitdupeln.
Alle Ergebnisse der Aufgabe können mit dem interaktiven Applet M–stufiges Phase Shift Keying und Union Bound per Simulation überprüft werden.

Fragebogen

$\phi_{\rm off}\ = \ $

$\ \rm Grad$

	$p_{\rm UB} = 4 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm UB} = 2 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm UB} = 2 \cdot {\rm Q}[\sqrt{2E_{\rm S}/N_0}\hspace{0.05cm}]$.

	$p_{\rm S} ≤ 4 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm S} ≤ 2 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm S} ≤ 2 \cdot {\rm Q}[\sqrt{2E_{\rm S}/N_0}\hspace{0.05cm}]$.

	$p_{\rm B} ≤ 2 \cdot {\rm Q}[\sqrt{2E_{\rm B}/N_0}\hspace{0.05cm}]$,
	$p_{\rm B} ≤ {\rm Q}[\sqrt{2E_{\rm B}/N_0}\hspace{0.05cm}]$,
	$p_{\rm B} ≤ {\rm Q}[\sqrt{E_{\rm B}/N_0}\hspace{0.05cm}]$.

Musterlösung

Solution

(1) Mit $M = 4$ lauten die Signalraumpunkte $\boldsymbol{s}_i = (s_{\rm I \it i}, s_{\rm Q \it i})$ der digitalen Phasenmodulation ($i = 0, \ \text{...} \ , 3$):

$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$

$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$

Mit $\phi_{\rm off} \ \underline {= \pi/2 \ (45^°)}$ ergeben sich genau die Signalraumpunkte der 4–QAM:

$$\boldsymbol{ s}_{\rm 0} = (+\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 1} = (-\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ s}_{\rm 3} = (-\sqrt{2}, -\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 4} = (+\sqrt{2}, -\sqrt{2}) \hspace{0.05cm}.$$

(2) Richtig ist der Lösungsvorschlag 2: Für die 4–PSK ergibt sich mit der vorne angegebenen Gleichung:

$$p_{\rm S} \le p_{\rm UB} \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] = 2 \cdot {\rm Q} \left [ { 1}/{ \sqrt{2}} \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ]= 2 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$

(3) Richtig ist der Lösungsvorschlag 2:

Die 4–QAM ist mit der 4–PSK identisch (hinsichtlich Fehlerwahrscheinlichkeit sogar unabhängig vom Phasenoffset).
Der Lösungsvorschlag 1 gibt dagegen die Union Bound der $M$–QAM allgemein an, wobei $M = 4$ eingesetzt ist.
Da es aber bei 4–QAM keine inneren Symbole gibt, ist diese Schranke zu pessimistisch.
Die sich ergebende "Union Bound" ist dann doppelt so groß wie die 4–PSK–Schranke.

(4) Hier ist wiederum der zweite Lösungsvorschlag richtig:

Bei Graycodierung führt jeder Symbolfehler zu einem Bitfehler, wenn man nur benachbarte Regionen betrachtet: $p_{\rm B} \approx p_{\rm S}/2$.
Außerdem gilt $E_{\rm S} = 2 \ E_{\rm B}$. Daraus folgt:

$$p_{\rm B} = \frac{p_{\rm S}}{2} \le {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$

Wie in der Musterlösung zur Aufgabe 4.13 hergeleitet, gilt sogar exakt:

$$p_{\rm B} = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$

Bei dieser Herleitung wurde verwendet, dass man die 4–QAM durch zwei orthogonale BPSK–Modulationen (mit Cosinus– bzw. Minus–Sinusträger) darstellen kann.
Somit ist die Bitfehlerwahrscheinlichkeit der 4–QAM und damit auch der 4–PSK in Abhängigkeit von $E_{\rm B}/N_0$ die gleiche wie für BPSK.