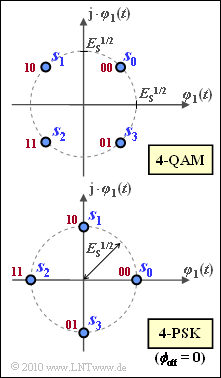
Exercise 4.14Z: 4-QAM and 4-PSK

• Return to book

Signal space constellation of 4-QAM and 4-PSK

For  "quadrature amplitude modulation"  ($M$–QAM), an upper bound ("Union–Bound")  on the symbol error probability was given in the theory section for  $M ≥ 16$: 

$$ p_{\rm UB} = 4 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$

In the theory section, one can also find the "Union–Bound" for  "M–level phase modulation"  (M–PSK)

$$ p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$

In both methods, each signal space point has exactly the same energy, namely  $E_{\rm S}$.

From the graph, one can see that for the special case  $M = 4$,  the two modulation processes should actually be identical, which is not directly evident from the above equations.

The 4–PSK is shown here with the phase offset  $\phi_{\rm off} = 0$.  With a general phase offset, on the other hand, the in-phase and quadrature components of the signal space points are generally:  $(i = 0, \ ... \ , M = 1)$:

$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$

$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  "Carrier Frequency Systems with Coherent Demodulation".
• Reference is made in particular to the sections  "Quadrature amplitude modulation"  and  "Multi-level phase modulation".
• In the above diagram the Gray mapping of the symbols to bit-duples is shown in red.
• All results of the exercise can be checked by simulation with the interactive applet "M–level Phase Shift Keying and Union Bound".

Questions

1

For which phase offset do the 4–QAM and the 4–PSK match exactly?

$\phi_{\rm off}\ = \ $ $\ \rm degree$

2

What is the upper bound  $($Union Bound,  $p_{\rm UB} ≥ p_{\rm S})$  for the 4–PSK?

	$p_{\rm UB} = 4 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm UB} = 2 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm UB} = 2 \cdot {\rm Q}[\sqrt{2E_{\rm S}/N_0}\hspace{0.05cm}]$.

3

Specify a closer upper bound for the 4–QAM.

	$p_{\rm S} ≤ 4 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm S} ≤ 2 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$,
	$p_{\rm S} ≤ 2 \cdot {\rm Q}[\sqrt{2E_{\rm S}/N_0}\hspace{0.05cm}]$.

4

What is the bit error probability bound for the 4–QAM, assuming Gray coding?

	$p_{\rm B} ≤ 2 \cdot {\rm Q}[\sqrt{2E_{\rm B}/N_0}\hspace{0.05cm}]$,
	$p_{\rm B} ≤ {\rm Q}[\sqrt{2E_{\rm B}/N_0}\hspace{0.05cm}]$,
	$p_{\rm B} ≤ {\rm Q}[\sqrt{E_{\rm B}/N_0}\hspace{0.05cm}]$.

Solution

Solution

(1)  With $M = 4$, the signal space points are $\boldsymbol{s}_i = (s_{\rm I \it i}, s_{\rm Q \it i})$ of digital phase modulation ($i = 0, \ \text{...} \ , 3$):

$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$

$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$

With $\phi_{\rm off} \ \underline {= \pi/2 \ (45^°)}$, we obtain exactly the signal space points of the 4–QAM:

$$\boldsymbol{ s}_{\rm 0} = (+\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 1} = (-\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ s}_{\rm 3} = (-\sqrt{2}, -\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 4} = (+\sqrt{2}, -\sqrt{2}) \hspace{0.05cm}.$$

(2)  Solution 2 is correct: For the 4–PSK, the equation given earlier gives:

$$p_{\rm S} \le p_{\rm UB} \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] = 2 \cdot {\rm Q} \left [ { 1}/{ \sqrt{2}} \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ]= 2 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$

(3)  Solution 2 is correct:

• The 4–QAM is identical with the 4–PSK (regarding error probability even independent of the phase offset).
• Solution 1, on the other hand, gives the Union Bound of the $M$–QAM in general, where $M = 4$ is used.
• However, since there are no inner symbols in 4–QAM, this bound is too pessimistic.
• The resulting "Union Bound" is then twice as large as the 4–PSK bound.

(4)  Here again the second solution is correct:

• In Gray coding, each symbol error results in a bit error if only adjacent regions are considered:   $p_{\rm B} \approx p_{\rm S}/2$.
• Furthermore, $E_{\rm S} = 2 \ E_{\rm B}$ is valid. It follows that

$$p_{\rm B} = \frac{p_{\rm S}}{2} \le {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$

• As derived in the solution to "Exercise 4.13", even exactly:

$$p_{\rm B} = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$

• In this derivation, it was used that the 4–QAM can be represented by two orthogonal BPSK modulations (with cosine and minus sinusoidal carriers, respectively).
• Thus, the bit error probability of the 4–QAM and thus also of the 4–PSK as a function of $E_{\rm B}/N_0$ is the same as for BPSK.