Exercise 2.1Z: Which Tables Describe Groups?
In this exercise we consider sets of three elements each, generally denoted by $\{z_0, \, z_1, \, z_2\}$. The elements can be:
- numbers, for example $z_0 = 0, \ z_1 = 1, \ z_2 = 2$,
- algebraic expressions, such as $z_0 = A, \ z_1 = B, \ z_2 = C$,
- anything, for example $z_0 = \ "\hspace{-0.05cm}{\rm apple}\hspace{0.05cm}", \ z_1 = \ "\hspace{-0.05cm}{\rm pear}\hspace{0.05cm}", \ z_2 = \ "\hspace{-0.05cm}{\rm lemon}\hspace{0.05cm}"$.
A group $(G, \ "+")$ with respect to the addition results if by a table the "$+$"–linkage between two elements each was defined in such a way that the following conditions are fulfilled (the run variables $i, \ j, \ k$ can take the values $0, \ 1, \ 2$ respectively):
- For all $z_i ∈ G$ and $z_j ∈ G$ holds $(z_i + z_j) ∈ G$ ⇒ Closure–criterion'. The condition must also be satisfied for $i = j$ .
- For all $z_i, \ z_j, \ z_k$, $(z_i + z_j) + z_k = z_i + (z_j + z_k)$ ⇒ Associative law'.
- There is a neutral element with respect to addition ⇒ $N_{\rm A} ∈ G$ such that for all $z_i ∈ G$ holds $z_i + N_{\rm A} = z_i$.
- For all $z_i ∈ G$ there is a inverse element with respect to addition ' ⇒ ${\rm Inv}_{\rm A}(z_i) ∈ G$ such that $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A}$ holds.
If, in addition, for all $z_i ∈ G$ and $z_j ∈ G$ still the commutative law' ⇒ $z_i + z_j = z_j + z_i$ is satisfied, then it is called a commutative group or – after the Norwegian mathematician Niels Hendrik Abel – an Abelian group.
The number set $\{0, \, 1, \, 2\}$ is an Abelian (commutative) group.
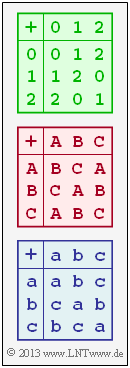
- According to the green bordered addition table in the above diagram, the addition modulo $3$ is to be understood here.
- So the sum is always $0, \ 1$ or $2$.
- The neutral element is $N_{\rm A} = 0$ and the to $z_i$ inverse element ${\rm Inv}_{\rm A}(z_i) = -z_i$:
- $${\rm Inv_A}(0) = 0 \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(1) = (-1)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 2 \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(2) = (-2)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 1 \hspace{0.05cm}.$$
In this exercise, you are to check whether the two other addition tables shown in the above diagram also each belong to an algebraic group.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Grundlagen der Algebra.
- Bezug genommen wird insbesondere auf die Seite Definition und Beispiele einer algebraischen Gruppe.
Fragebogen
Musterlösung
- Das neutrale Element $N_{\rm A} = {\rm C}$ erkennt man aus der letzten Zeile der Additionstabelle.
- Aus der Bedingung $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A} = {\rm C}$ erhält man:
- $\rm Inv_A(A) = B$, da an der zweiten Stelle der ersten Zeile das einzige $\rm C$ steht,
- $\rm Inv_A(B) = A$, da an der ersten Stelle der zweiten Zeile das einzige $\rm C$ steht,
- $\rm Inv_A(C) = C$, da an der letzten Stelle der dritten Zeile das einzige $\rm C$ steht.
- Das Assoziativgesetz überprüfen wir (unzulässigerweise) nur an einem einzigen Beispiel. Durch zweimalige Anwendung der Additionstabelle erhält man beispielsweise $\rm (A + B) + C = C + C=C$. Das gleiche Ergebnis ergibt sich für $\rm A + (B + C) = A + B = C$.
Damit sind alle Bedingungen für eine additive Gruppe erfüllt. Die Gültigkeit des Kommutativgesetzes erkennt man aus der Symmetrie der Additionstabelle zur Diagonalen. Damit ist die Gruppe auch "abelsch".
Übrigens: Die (rote) Additionstabelle ergibt sich aus der grünen Tabelle durch die Umbenennungen $0 → \rm C, \ 1 → A$ und $2 → \rm B$ und anschließender $\rm ABC$–Sortierung.
(2) Richtig ist Nein:
- Alle Aussagen sind allein durch die Additionstabelle bestimmt und nicht durch die Bedeutung der Elemente.
- Auch der Autor dieser Aufgabe kann allerdings nicht tiefergehend begründen, warum die Modulo–3–Addition von "$\rm Apfel$" und "$\rm Birne$" das neutrale Element "$\rm Citrone$" ergibt.
(3) Die beiden ersten Aussagen treffen zu im Gegensatz zur letzten:
- Das Kommutativgesetz wird verletzt (keine Symmetrie bezüglich der Tabellendiagonalen). Beispielsweise gilt:
- $$ {\rm a} + {\rm b} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm b} + {\rm a} = {\rm c} \hspace{0.05cm},$$
- $${\rm a} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$
- $${\rm b} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm b} = {\rm c} \hspace{0.05cm} \hspace{0.05cm}.$$
- Damit ist die hier betrachtete Verknüpfung keine Abelsche (kommutative) Gruppe.
- Mehr noch, wegen der Verletzung des Assoziativgesetzes liegen hier bereits die Grundvoraussetzungen einer Gruppe nicht vor. Beispielsweise gilt:
- $${\rm c} + ({\rm c} + {\rm c}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$
- $$({\rm c} + {\rm c}) + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm a} + {\rm c} = {\rm c} \hspace{0.05cm}.$$