Exercise 2.2: Properties of Galois Fields

Addition / Multiplikation für $q = 5$ und $q = 6$

Wir betrachten hier die Zahlenmengen

$Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
$Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.

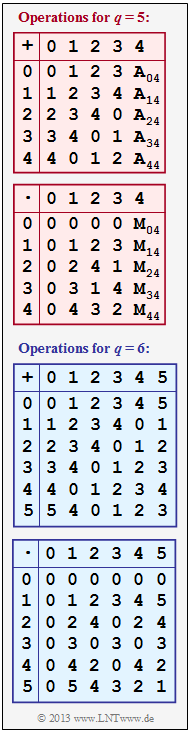
In nebenstehender Grafik sind die (teilweise unvollständigen) Additions– und Multiplikationstabellen für $q = 5$ und $q = 6$ angegeben, wobei sowohl die Addition ("$+$") als auch die Multiplikation ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$") modulo $q$ zu verstehen sind.

Zu überprüfen ist, ob die Zahlenmengen $Z_5$ und $Z_6$ alle Bedingungen eines Galoisfeldes $\rm GF(5)$ bzw. $\rm GF(6)$ erfüllen.

Im Theorieteil werden insgesamt acht Bedingungen genannt, die alle erfüllt sein müssen. Sie sollen nur zwei dieser Bedingungen überprüfen:

$\rm(D)$ Für alle Elemente gibt es eine additive Inverse (Inverse for "$+$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$

$\rm(E)$ Alle Elemente haben eine multiplikative Inverse (Inverse for "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$

Die weiteren Bedingungen für ein Galoisfeld, nämlich

Closure,
Existenz von Null– und Einselelement,
Gültigkeit von Kommutativ–, Assoziativ– und Distributivgesetz

werden sowohl von $Z_5$ als auch von $Z_6$ erfüllt.

Hinweis:

Die Aufgabe bezieht sich auf das Kapitel Einige Grundlagen der Algebra.

Fragebogen

$A_{04} \ = \ $

$A_{14} \ = \ $

$A_{44} \ = \ $

$M_{04} \ = \ $

$M_{14} \ = \ $

$M_{44} \ = \ $

	Ja.
	Nein, es gibt nicht für alle Elemente $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$ eine additive Inverse.
	Nein, die Elemente $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$ haben nicht alle eine multiplikative Inverse.

	Ja.
	Nein, es gibt nicht für alle Elemente $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$ eine additive Inverse.
	Nein, die Elemente $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$ haben nicht alle eine multiplikative Inverse.

	$Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ ist ein Galoisfeld?
	$Z_{11} = \{0, \, 1, \, 2, \, 3, \, 4, \,5, \, 6, \, 7, \, 8, \, 9, \, 10\}$ ist ein Galoisfeld?
	$Z_{12} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10, \, 11\}$ ist ein Galoisfeld?

Musterlösung

Solution

(1) Allgemein gilt für $0 ≤ \mu ≤ 4 \text{:} \hspace{0.2cm} A_{\mu 4} = (\mu + 4) \, {\rm mod} \, 5$. Daraus folgt:

$$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$

$$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$

Aufgrund des Kommutativgesetzes der Addition,

$$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm f\ddot{u}r \hspace{0.2cm}alle\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$

ist natürlich die letzte Spalte der Additionstabelle identisch mit der letzten Zeile der gleichen Tabelle.

(2) Nun gilt $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$ und man erhält:

$$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$

$$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$

Da die Multiplikation ebenfalls kommutativ ist, stimmt auch in der Multiplikationstabelle die letzte Spalte wieder mit der letzten Zeile überein.

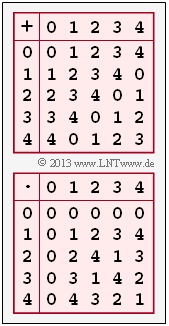
Tabellen zur Addition und Multiplikation für $q = 5$

(3) Die Grafik zeigt die vollständigen Additions– und Multiplikationstabellen für $q = 5$. Man erkennt:

In der Additionstabelle gibt es in jeder Zeile (und auch in jeder Spalte) genau eine Null. Zu jedem $z_i ∈ Z_5$ gibt es also ein ${\rm Inv}_{\rm A} (z_i)$, das die Bedingung $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$ erfüllt:

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-3) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$

In der Multiplikationstabelle lassen wir das Nullelement (erste Zeile und erste Spalte) außer Betracht. In allen anderen Zeilen und Spalten der unteren Tabelle gibt es tatsächlich jeweils genau eine Eins. Aus der Bedingung $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$ erhält man:

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$

Da sowohl die erforderlichen additiven als auch die multiplikativen Inversen existieren beschreibt $Z_5$ ein Galoisfeld $\rm GF(5)$

⇒ Richtig ist der Lösungsvorschlag 1.

(4) Aus der blauen Additionstabelle auf der Angabenseite erkennt man, dass alle Zahlen $0, \, 1, \, 2, \, 3, \, 4, \, 5$ der Menge $Z_6$ eine additive Inverse besitzen ⇒ in jeder Zeile (und Spalte) gibt es genau eine Null.

Eine multiplikative Inverse ${\rm Inv}_{\rm M}(z_i)$ gibt es dagegen nur für $z_i = 1$ und $z_i = 5$, nämlich

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$

Für $z_i = 2, \ z_i = 3$ und $z_i = 4$ findet man dagegen kein Element $z_j$, so dass $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$ ergibt.

Richtig ist also der Lösungsvorschlag 3 ⇒ Die blauen Tabellen für $q = 6$ ergeben kein Galoisfeld $\rm GF(6)$.

(5) Richtig ist der Lösungsvorschlag 2:

Eine endliche Zahlenmenge $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$ natürlicher Zahlen führt nur dann zu einem "endlichen Zahlenkörper" (dies ist die deutsche Bezeichnung für ein Galoisfeld), wenn $q$ eine Primzahl ist.
Von den oben genannten Zahlenmengen trifft dies nur auf $Z_{11}$ zu.