Exercise 2.2: Properties of Galois Fields

Addition / multiplication for $q = 5$ and $q = 6$

Here we consider the sets of numbers

$Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
$Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.

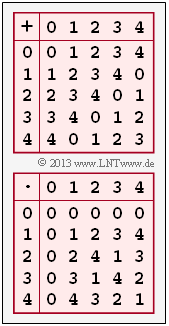
In the adjacent graph, the (partially incomplete) addition– and multiplication tables for $q = 5$ and $q = 6$ are given, where both addition ("$+$") and multiplication ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$") modulo $q$ are to be understood.

To be checked is whether the sets of numbers $Z_5$ and $Z_6$ satisfy all the conditions of a Galois field $\rm GF(5)$ and $\rm GF(6)$ respectively.

In the "theory section" a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions:

$\rm(D)$ For all elements there is an additive inverse (Inverse for "$+$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$

$\rm(E)$ All elements have a multiplicative inverse (Inverse for "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"):

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$

The other conditions for a Galois field, viz.

Closure,
Existence of zero– and identity element,
validity of commutative–, associative– and distributive law

are satisfied by both $Z_5$ and $Z_6$.

Hints:

The exercise refers to the chapter Some Basics of Algebra.

Questions

$A_{04} \ = \ $

$A_{14} \ = \ $

$A_{44} \ = \ $

$M_{04} \ = \ $

$M_{14} \ = \ $

$M_{44} \ = \ $

	Yes.
	No, there is not an additive inverse for all elements $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$ .
	No, the elements $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$ do not all have a multiplicative inverse.

	Yes.
	No, there is not an additive inverse for all elements $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$ .
	No, the elements $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$ do not all have a multiplicative inverse.

	$Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field?
	$Z_{11} = \{0, \, 1, \, 2, \, 3, \, 4, \,5, \, 6, \, 7, \, 8, \, 9, \, 10\}$ is a Galois field?
	$Z_{12} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9, \, 10, \, 11\}$ is a Galois field?

Musterlösung

Solution

(1) Allgemein gilt für $0 ≤ \mu ≤ 4 \text{:} \hspace{0.2cm} A_{\mu 4} = (\mu + 4) \, {\rm mod} \, 5$. Daraus folgt:

$$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$

$$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$

Aufgrund des Kommutativgesetzes der Addition,

$$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm f\ddot{u}r \hspace{0.2cm}alle\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$

ist natürlich die letzte Spalte der Additionstabelle identisch mit der letzten Zeile der gleichen Tabelle.

(2) Nun gilt $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$ und man erhält:

$$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$

$$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$

Da die Multiplikation ebenfalls kommutativ ist, stimmt auch in der Multiplikationstabelle die letzte Spalte wieder mit der letzten Zeile überein.

Tabellen zur Addition und Multiplikation für $q = 5$

(3) Die Grafik zeigt die vollständigen Additions– und Multiplikationstabellen für $q = 5$. Man erkennt:

In der Additionstabelle gibt es in jeder Zeile (und auch in jeder Spalte) genau eine Null. Zu jedem $z_i ∈ Z_5$ gibt es also ein ${\rm Inv}_{\rm A} (z_i)$, das die Bedingung $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$ erfüllt:

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-3) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$

In der Multiplikationstabelle lassen wir das Nullelement (erste Zeile und erste Spalte) außer Betracht. In allen anderen Zeilen und Spalten der unteren Tabelle gibt es tatsächlich jeweils genau eine Eins. Aus der Bedingung $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$ erhält man:

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$

Da sowohl die erforderlichen additiven als auch die multiplikativen Inversen existieren beschreibt $Z_5$ ein Galoisfeld $\rm GF(5)$

⇒ Richtig ist der Lösungsvorschlag 1.

(4) Aus der blauen Additionstabelle auf der Angabenseite erkennt man, dass alle Zahlen $0, \, 1, \, 2, \, 3, \, 4, \, 5$ der Menge $Z_6$ eine additive Inverse besitzen ⇒ in jeder Zeile (und Spalte) gibt es genau eine Null.

Eine multiplikative Inverse ${\rm Inv}_{\rm M}(z_i)$ gibt es dagegen nur für $z_i = 1$ und $z_i = 5$, nämlich

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$

$$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$

Für $z_i = 2, \ z_i = 3$ und $z_i = 4$ findet man dagegen kein Element $z_j$, so dass $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$ ergibt.

Richtig ist also der Lösungsvorschlag 3 ⇒ Die blauen Tabellen für $q = 6$ ergeben kein Galoisfeld $\rm GF(6)$.

(5) Richtig ist der Lösungsvorschlag 2:

Eine endliche Zahlenmenge $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$ natürlicher Zahlen führt nur dann zu einem "endlichen Zahlenkörper" (dies ist die deutsche Bezeichnung für ein Galoisfeld), wenn $q$ eine Primzahl ist.
Von den oben genannten Zahlenmengen trifft dies nur auf $Z_{11}$ zu.