Exercise 5.3: AWGN and BSC Model
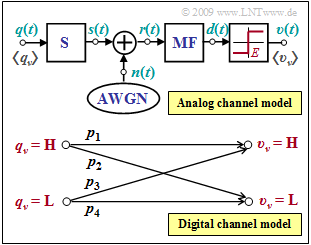
The upper graphic shows the analog channel model of a digital transmission system, where the additive noise signal $n(t)$ with the $($two-sided$)$ noise power density $N_0/2$ is effective. This is AWGN noise. The variance of the noise component before the decision $($after the matched filter$)$ is then
- $$\sigma^2 = \frac{N_0}{2T} \hspace{0.05cm}.$$
Further, let hold:
- No intersymbol interference occurs. If the symbol $q_{\nu} = \mathbf{H}$ was sent, the useful component of the detection signal is equal to $+s_0$, while for $q_{\nu} = \mathbf{L}$, it is equal to $-s_0$.
- The threshold decision takes into account a threshold drift, that is, the threshold $E$ may well deviate from the optimal value $E = 0$. The "decision rule" is:
- $$\upsilon_\nu = \left\{ \begin{array}{c} \mathbf{H} \\ \mathbf{L} \end{array} \right.\quad \begin{array}{*{1}c} {\rm if}\hspace{0.15cm}d (\nu \cdot T) > E \hspace{0.05cm}, \\ {\rm if} \hspace{0.15cm} d (\nu \cdot T) \le E\hspace{0.05cm}.\\ \end{array}$$
- With the threshold value $E = 0$, the mean error probability is given by
- $$p_{\rm M} = {\rm Q} \left ( {s_0}/{\sigma} \right ) = 0.01\hspace{0.05cm}.$$
⇒ The bottom graph shows a digital channel model characterized by the four transition probabilities $p_1, p_2, p_3$ and $p_4$. This is to be fitted to the analog channel model.
Notes:
- The exercise belongs to the chapter "Binary Symmetric Channel".
- Numerical values of the Q–function can be determined with the interactive applet "Complementary Gaussian Error Functions".
Questions
Solution
- From this it follows for the quotient of the detection useful sample value and the detection noise rms value:
- $${s_0}/{\sigma}= {\rm Q}^{-1} \left ( 0.01 \right ) \hspace{0.15cm}\underline {\approx 2.32}\hspace{0.05cm}.$$
(2) With $E = 0$, the probabilities of the given digital channel model are given by:
- $$p_2 = p_3 = p = 0.01 \hspace{0.05cm}, \hspace{0.2cm}p_1 = p_4 = 1-p = 0.99\hspace{0.05cm}.$$
- A comparison with the theory part shows that this channel model corresponds to the BSC model, independent of the statistics of the source symbols.
- Thus, both solutions are correct.
(3) The transition probability $p_2$ now describes the case where the decision threshold $E = 0.25 \cdot s_0$ was mistakenly undershot.
- Then $v_{\nu} = \mathbf{L}$, although $q_{\nu} = \mathbf{H}$ was sent. Thus, the distance from the threshold is only $0.75 \cdot s_0$ and it holds:
- $$p_{\rm 2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm Q} \left ( \frac{0.75 \cdot s_0}{\sigma} \right ) = {\rm Q} \left ( 0.75 \cdot 2.32 \right ) = {\rm Q} \left ( 1.74 \right )\hspace{0.15cm}\underline {\approx 0.041}\hspace{0.05cm}, \hspace{0.5cm} p_{\rm 1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}1 - p_{\rm 2} \hspace{0.15cm}\underline {= 0.959}\hspace{0.05cm}.$$
- Similarly, the transition probabilities $p_3$ and $p_4$ can be calculated, now assuming the threshold distance $1.25 \cdot s_0$:
- $$p_{\rm 3} = {\rm Q} \left ( 1.25 \cdot 2.32 \right ) = {\rm Q} \left ( 2.90 \right )\hspace{0.15cm}\underline {\approx 0.002}\hspace{0.05cm}, \hspace{0.2cm} p_{\rm 4} = 1 - p_{\rm 3}\hspace{0.15cm}\underline { = 0.998}\hspace{0.05cm}.$$
(4) Neither of the two solutions applies:
- With the decision threshold $E ≠ 0$, the BSC model is not applicable regardless of the symbol statistic,
- since the symmetry property of the channel (the "S" flag in "BSC") does not hold.
(5) Statements 1 and 3 are true, but statement 2 is not:
- In the BSC model, $p_{\rm M} = 1\%$ is independent of the symbol probabilities $p_{\rm L}$ and $p_{\rm H}$.
- In contrast, for $p_{\rm L} = 0.9$, $p_{\rm H} = 0.1$ and $E = +s_0/4$:
- $$p_{\rm M} = 0.9 \cdot p_{\rm 3} + 0.1 \cdot p_{\rm 2}= 0.9 \cdot 0.2\% + 0.1 \cdot 4.1\% \approx 0.59\% \hspace{0.05cm}.$$
- The minimum results for $p_{\rm L} = 0.93$ and $p_{\rm H} = 0.07$ to $p_{\rm M} \approx 0.45\%$.