Exercise 2.15: Block Error Probability with AWGN

Unvollständige Ergebnistabelle

Am Beispiel des $\rm RSC \, (7, \, 3, \, 5)_8$ mit den Parametern

$n = 7$ (Anzahl der Codesymbole),
$k =3$ (Anzahl der Informationssymbole),
$t = 2$ (Korrekturfähigkeit)

soll die Berechnung der Blockfehlerwahrscheinlichkeit beim Bounded Distance Decoding (BDD) gezeigt werden. Die entsprechende Gleichung lautet:

$${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} \ne \underline{u}) = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$

Die Berechnung erfolgt für den AWGN–Kanal, der durch den Parameter $E_{\rm B}/N_0$ gekennzeichnet ist.

Der Quotient $E_{\rm B}/{N_0}$ lässt sich über die Beziehung

$$\varepsilon = {\rm Q} \big (\sqrt{{2 \cdot R \cdot E_{\rm B}}/{N_0}} \big ) $$

in das BSC–Modell überführen, wobei $R$ die Coderate bezeichnet $($hier: $R = 3/7)$ und ${\rm Q}(x)$ das komplementäre Gaußsche Fehlerintegral angibt.

Da aber beim betrachteten Code die Symbole aus $\rm GF(2^3)$ entstammen, muss das BSC–Modell mit Parameter $\varepsilon$ ebenfalls noch an die Aufgabenstellung adaptiert werden.
Für die Verfälschungwahrscheinlichkeit des $m$–BSC–Modells gilt, wobei hier $m = 3$ zu setzen ist (drei Bit pro Codesymbol):

$$\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m \hspace{0.05cm}.$$

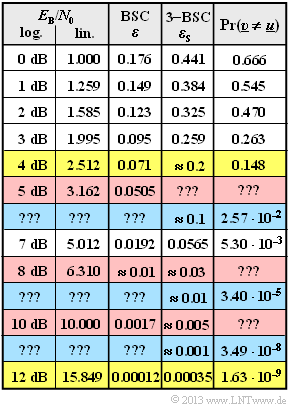
Für einige $E_{\rm B}/N_0$–Werte sind die Ergebnisse in obiger Tabelle eingetragen. Die beiden gelb hinterlegten Zeilen werden hier kurz erläutert:

Für $10 \cdot \lg {E_{\rm B}/N_0} = 4 \ \rm dB$ ergibt sich $\varepsilon \approx {\rm Q}(1.47) \approx 0.071$ und $\varepsilon_{\rm S} \approx 0.2$. Die Blockfehlerwahrscheinlichkeit kann hier am einfachsten über das Komplement berechnet werden:

$${\rm Pr(Blockfehler)} = 1 - \left [ {7 \choose 0} \cdot 0.8^7 + {7 \choose 1} \cdot 0.2 \cdot 0.8^6 + {7 \choose 2} \cdot 0.2^2 \cdot 0.8^5\right ] \approx 0.148 \hspace{0.05cm}.$$

Für $10 \cdot \lg {E_{\rm B}/N_0} = 12 \ \rm dB$ erhält man $\varepsilon \approx 1.2 \cdot 10^{-4}$ und $\varepsilon_{\rm S} \approx 3.5 \cdot 10^{-4}$. Mit dieser sehr kleinen Verfälschungswahrscheinlichkeit dominiert der $f = 3$–Term, und man erhält:

$${\rm Pr(Blockfehler)} \approx {7 \choose 3} \cdot (3.5 \cdot 10^{-4})^3 \cdot (1- 3.5 \cdot 10^{-4})^4 \approx 1.63 \cdot 10^{-9} \hspace{0.05cm}.$$

Sie sollen für die rot hinterlegten Zeilen $(10 \cdot \lg {E_{\rm B}/N_0} = 5 \ \rm dB, \ 8 \ dB$, $10 \ \rm dB)$ die Blockfehlerwahrscheinlichkeiten berechnen.
Die blau hinterlegten Zeilen zeigen einige Ergebnisse der Aufgabe 2.15Z. Dort wird ${\rm Pr}(\underline{v} ≠ \underline{u})$ für $\varepsilon_{\rm S} = 10\%, \ 1\%$ $0.1\%$ berechnet.
In den Teilaufgaben (4) und (5) sollen Sie den Zusammenhang zwischen der Größe $\varepsilon_{\rm S}$ und dem AWGN–Parameter $E_{\rm B}/N_0$ herstellen und somit die obige Tabelle vervollständigen.

Hinweise:

Die Aufgabe gehört zum Kapitel Fehlerwahrscheinlichkeit und Anwendungsgebiete.
Wir verweisen Sie hier auf die beiden interaktive Applets

Komplementäre Gaußsche Fehlerfunktionen und

Binomial- und Poissonverteilung.

Fragebogen

${\rm Pr(Blockfehler)} \ = \ $

$\ \cdot 10^{-2}$

${\rm Pr(Blockfehler)} \ = \ $

$\ \cdot 10^{-4}$

${\rm Pr(Blockfehler)} \ = \ $

$\ \cdot 10^{-6}$

$\varepsilon_{\rm S} = 10^{-1} \text{:} \hspace{0.4cm} 10 \cdot \lg {E_{\rm B}/N_0} \ = \ $

$\ \rm dB$

$\varepsilon_{\rm S} = 10^{-2} \text{:} \hspace{0.4cm} 10 \cdot \lg {E_{\rm B}/N_0} \ = \ $

$\ \rm dB$

$\varepsilon_{\rm S} = 10^{-3} \text{:} \hspace{0.4cm} 10 \cdot \lg {E_{\rm B}/N_0} \ = \ $

$\ \rm dB$

Musterlösung

Solution

(1) Aus der Tabelle auf der Angabenseite kann der BSC–Parameter $\varepsilon = 0.0505$ abgelesen werden.

Damit erhält man für die Symbolverfälschungswahrscheinlichkeit $\varepsilon_{\rm S}$ mit $m = 3$:

$$1 - \varepsilon_{\rm S} = (1 - 0.0505)^3 \approx 0.856 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \varepsilon_{\rm S} \approx 0.144 \hspace{0.05cm}.$$

Der schnellste Weg zur Berechnung der Blockfehlerwahrscheinlichkeit führt hier über die Formel

$${\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 - {\rm Pr}(f=0) - {\rm Pr}(f=1) - {\rm Pr}(f=2) = 1 - 1 \cdot 0.856^7 - 7 \cdot 0.144^1 \cdot 0.856^6 - 21 \cdot 0.144^2 \cdot 0.856^5$$

$$\Rightarrow \hspace{0.3cm} {\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{v} \ne \underline{u}) =1 - 0.3368 - 0.3965 - 0.2001 \hspace{0.15cm} \underline{=0.0666} \hspace{0.05cm}.$$

(2) Nach gleichem Rechengang wie in Teilaufgabe (1) ergibt sich mit $\varepsilon_{\rm S} \approx 0.03 \ \Rightarrow \ 1 - \varepsilon_{\rm S} = 0.97$:

$${\rm Pr(Blockfehler)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \hspace{-0.05cm}-\hspace{-0.05cm} 1 \cdot 0.97^7 \hspace{-0.05cm}-\hspace{-0.05cm} 7 \cdot 0.03^1 \cdot 0.97^6 \hspace{-0.05cm}-\hspace{-0.05cm} 21 \cdot 0.03^2 \cdot 0.97^5 =1 \hspace{-0.05cm}-\hspace{-0.05cm} 0.8080 \hspace{-0.05cm}-\hspace{-0.05cm} 0.1749\hspace{-0.05cm}-\hspace{-0.05cm} 0.0162= 1 \hspace{-0.05cm}-\hspace{-0.05cm} 0.9991 = 9 \cdot 10^{-4} \hspace{0.05cm}.$$

Man sieht, dass hier die Differenz zwischen zwei fast gleich großen Zahlen gebildet werden muss, so dass das Ergebnis mit einem Fehler behaftet sein könnte.
Deshalb berechnen wir noch folgende Größen:

$${\rm Pr}(f=3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 3} \cdot \varepsilon_{\rm S}^3 \cdot (1 - \varepsilon_{\rm S})^4 = 35 \cdot 0.03^3 \cdot 0.97^4 = 8.366 \cdot 10^{-4}\hspace{0.05cm},$$

$${\rm Pr}(f=4) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 4} \cdot \varepsilon_{\rm S}^4 \cdot (1 - \varepsilon_{\rm S})^3 = 35 \cdot 0.03^4 \cdot 0.97^3 = 0.259 \cdot 10^{-4}\hspace{0.05cm},$$

$${\rm Pr}(f=5) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 5} \cdot \varepsilon_{\rm S}^5 \cdot (1 - \varepsilon_{\rm S})^2 = 21 \cdot 0.03^5 \cdot 0.97^2 = 0.005 \cdot 10^{-4}$$

$$\Rightarrow \hspace{0.3cm} {\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} \ne \underline{u}) \approx {\rm Pr}(f=3) + {\rm Pr}(f=4) + {\rm Pr}(f=5) \hspace{0.15cm} \underline{=8.63 \cdot 10^{-4}} \hspace{0.05cm}.$$

Auf die Terme für $f = 6$ und $f = 7$ kann hier verzichtet werden. Sie liefern keinen relevanten Beitrag.

(3) Hier ist bereits $\varepsilon_{\rm S} = 0.005 \ \Rightarrow \ 1 - \varepsilon_{\rm S} = 0.995$ in der Tabelle vorgegeben.

Der (weitaus) dominierende Term bei der Berechnung der Blockfehlerwahrscheinlichkeit ist ${\rm Pr}(f = 3)$:

$${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} \ne \underline{u}) \approx {\rm Pr}(f=3) = {7 \choose 3} \cdot 0.005^3 \cdot 0.995^4 \hspace{0.15cm} \underline{\approx 4.3 \cdot 10^{-6}} \hspace{0.05cm}.$$

(4) Für den BSC–Parameter $\varepsilon$ gilt mit $\varepsilon_{\rm S} = 0.1$:

$$\varepsilon = 1 -(1 - \varepsilon_{\rm S})^{1/3} = 1 - 0.9^{1/3} \approx 0.0345 \hspace{0.05cm}.$$

Der Zusammenhang zwischen $\varepsilon$ und $E_{\rm B}/N_0$ lautet:

$$\varepsilon = {\rm Q}(x)\hspace{0.05cm}, \hspace{0.5cm} x = \sqrt{2 \cdot R \cdot E_{\rm B}/N_0}\hspace{0.05cm}.$$

Die Inverse $x = {\rm Q}^{-1}(0.0345)$ ergibt sich mit dem Applet Komplementäre Gaußsche Fehlerfunktionen zu $x = 1.82$.
Damit erhält man weiter:

$$E_{\rm B}/N_0 = \frac{x^2}{2R} = \frac{1.82^2}{2R \cdot 3/7} \approx 3.864 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}(E_{\rm B}/N_0) \hspace{0.15cm} \underline{\approx 5.87 \,\, {\rm dB}} \hspace{0.05cm}. $$

(5) Nach gleicher Rechnung erhält man

für $\varepsilon_{\rm S} = 10^{-2} \ \Rightarrow \ \varepsilon \approx 0.33 \cdot 10^{-2} \ \Rightarrow \ x = {\rm Q}^{-1}(\varepsilon) = 2.71$

$$E_{\rm B}/N_0 = \frac{x^2}{2R} = \frac{2.71^2}{2R \cdot 3/7} \approx 8.568 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}(E_{\rm B}/N_0) \hspace{0.15cm} \underline{\approx 9.32 \,\, {\rm dB}} \hspace{0.05cm}, $$

für $\varepsilon_{\rm S} = 10^{-3} \ \Rightarrow \ \varepsilon \approx 0.33 \cdot 10^{-3} \ \Rightarrow \ x = {\rm Q}^{-1}(\varepsilon) = 3.4$:

$$E_{\rm B}/N_0 = \frac{x^2}{2R} = \frac{3.4^2}{2R \cdot 3/7} \approx 13.487 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}(E_{\rm B}/N_0) \hspace{0.15cm} \underline{\approx 11.3 \,\, {\rm dB}} \hspace{0.05cm}. $$

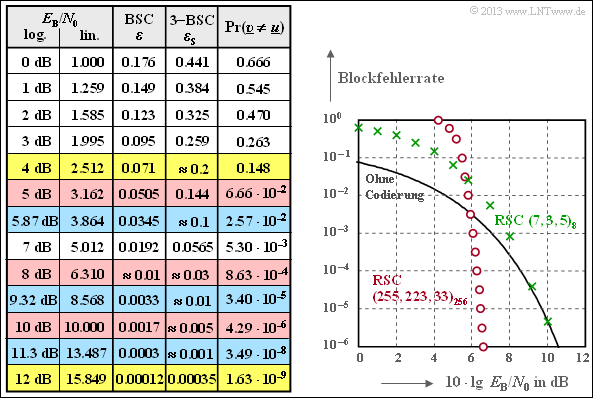
Ergebnisse zur $\rm RSC \, (7, \, 3, \, 5)_8$–Decodierung

Die Grafik zeigt den Verlauf der Blockfehlerwahrscheinlichkeit in Abhängigkeit von $10 \cdot \lg {E_{\rm B}/N_0}$ sowie die vollständig ausgefüllte Ergebnistabelle.

Man erkennt das deutlich ungünstigere (asymptotische) Verhalten dieses kurzen (grünen) Codes $\rm RSC \, (7, \, 5, \, 3)_8$ gegenüber dem (roten) Vergleichscode $\rm RSC \, (255, \, 223, \, 33)_8$:

Für Abszissenwerte kleiner als $10 \ \rm dB$ ergibt sich sogar ein schlechteres Ergebnis als ohne Codierung.
Deshalb soll hier nochmals darauf hingewiesen werden, dass dieser $\rm RSC \, (7, \, 3, \, 5)_8$ wenig praktische Bedeutung hat.
Er wurde für diese Aufgabe nur deshalb ausgewählt, um mit vertretbarem Aufwand die Berechnung der Blockfehlerwahrscheinlichkeit bei Bounded Distance Decoding (BDD) demonstrieren zu können.